011.重要排序算法的总结

前置知识：之前讲的所有排序

稳定性 §

排序算法的稳定性是指：同样大小的样本在排序之后不会改变原始的相对次序

• 稳定性对基础类型对象来说毫无意义
• 稳定性对非基础类型对象有意义，可以保留之前的相对次序

比如，每个数据有 name、age 两个属性，先按 name 排序后再按 age 排序，稳定的排序可以做到元素先按 age 排序，age 相等的元素按 name 排序

[
	{ name: 'C', age: '18' },
	{ name: 'B', age: '19' },
	{ name: 'A', age: '18' },
]
 
// 按 name 排序后
[
	{ name: 'A', age: '18' },
	{ name: 'B', age: '19' },
	{ name: 'C', age: '18' },
]
 
// 再按 age 排序
 
// 有稳定性：可以保证 name 顺序保持原样（不被打乱）
[
	{ name: 'A', age: '18' },
	{ name: 'C', age: '18' },
	{ name: 'B', age: '19' },
]
 
// 无稳定性：name 的顺序可能会被打乱
[
	{ name: 'C', age: '18' },
	{ name: 'A', age: '18' }, // A、C 顺序可能被打乱
	{ name: 'B', age: '19' },
]

主要排序算法对比 §

	时间	空间	稳定性
SelectionSort	$O(n^2)$	$O(1)$	无
BubbleSort	$O(n^2)$	$O(1)$	有
InsertionSort	$O(n^2)$	$O(1)$	有
MergeSort	$O(n\ast lo{g}^n)$	$O(n)$	有
QuickSort	$O(n\ast lo{g}^n)$	$O(lo{g}^n)$	无
HeapSort	$O(n\ast lo{g}^n)$	$O(1)$	无
CountSort	$O(n)$	$O(m)$	有
RadixSort	$O(n)$	$O(n+m)$	有

注意：随机快速排序的复杂度一定要按照概率上的期望指标来估计，用最差的复杂度估计无意义

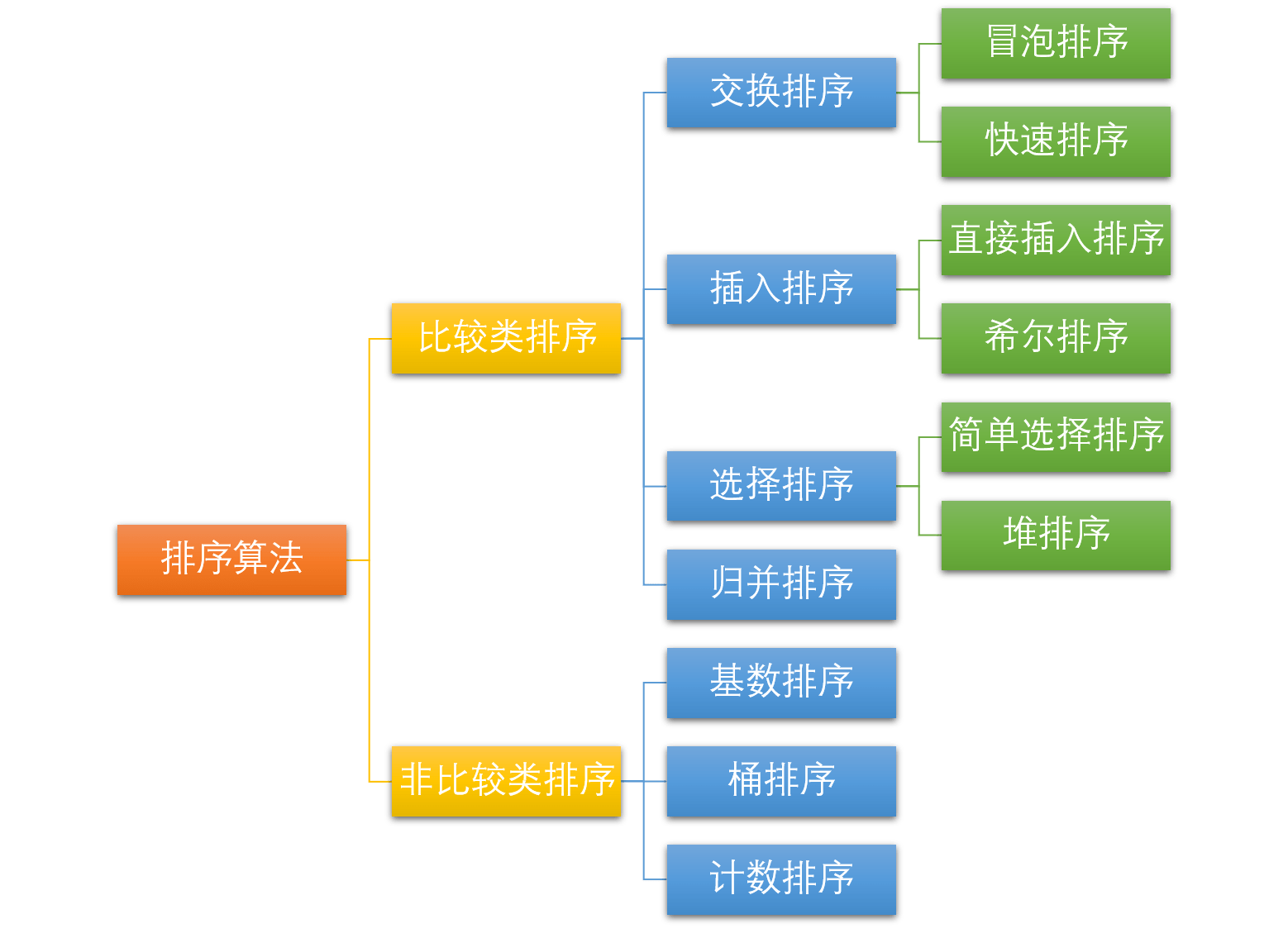
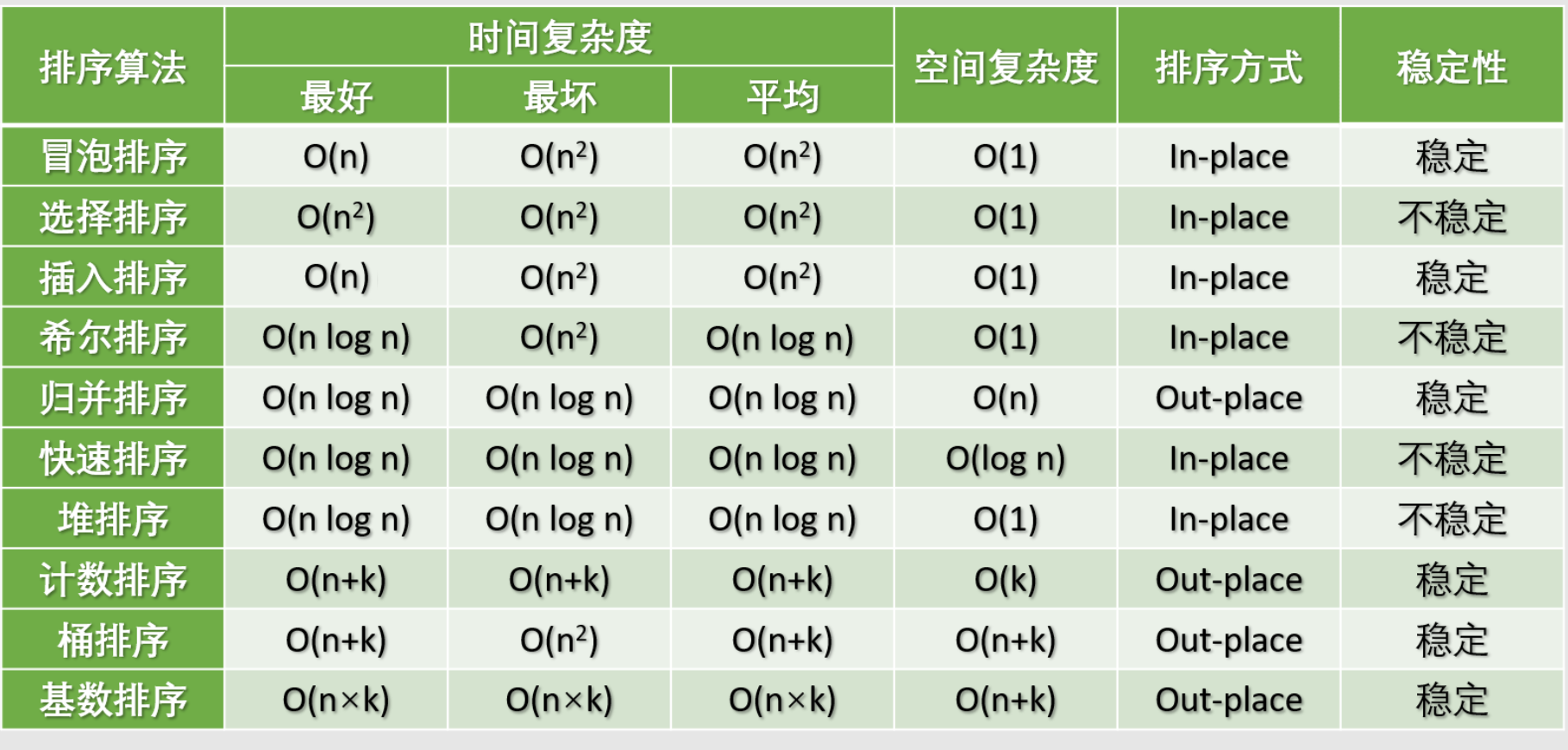
图片名词解释：

• n：数据规模
• k：“桶” 的个数
• In-place：占用常数内存，不占用额外内存
• Out-place：占用额外内存

其他排序算法 §

基于比较的排序，时间复杂度 $O(n\ast lo{g}^n)$，空间复杂度低于 $O(n)$，还具有稳定性的排序算法，目前没有找到

TimSort 也不行，虽然在实际应用中 TimSort 通常不需要这么多的额外空间，但空间复杂度指标就是 $O(n)$

有兴趣的同学可以研究，但是在算法面试、笔试、比赛中都很少用到 TimSort 算法

同时还有希尔排序（ShellSort）也不常用，有兴趣的同学可以研究一下，就是加入步长调整的插入排序

// 希尔排序
func shellSort(nums []int) {
	n := len(nums)
	for gap := n >> 1; gap > 0; gap >>= 1 {
		for i := gap; i < n; i++ {
			for j := i - gap; j >= 0 && nums[j] > nums[j+gap]; j -= gap {
				nums[j], nums[j+gap] = nums[j+gap], nums[j]
			}
		}
	}
}

• 时间复杂度：$O(n\ast lo{g}^n)$
• 空间复杂度：$O(1)$
• 不稳定

如何选择排序算法 §

一切看你在排序过程中在乎什么

• 数据量非常小的情况下可以做到非常迅速：插入排序
• 性能优异、实现简单且利于改进（面对不同业务可以选择不同划分策略）、不在乎稳定性：随机快排
• 性能优异、不在乎额外空间占用、具有稳定性：归并排序
• 性能优异、额外空间占用要求 $O(1)$、不在乎稳定性：堆排序