前置知识：基本二分搜索、对数器、进一步了解对数器

二分答案法

正着不好求，反着推：当答案固定时，条件够不够用

估计最终答案可能的范围是什么，可以定的粗略，反正二分不了几次
分析问题的答案和给定条件之间的单调性，大部分时候只需要用到自然智慧
建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标
在最终答案可能的范围上不断二分搜索，每次用 f 函数判断，直到二分结束，找到最合适的答案

核心点：分析单调性、建立 f 函数

注意：这个技巧常用且重要，一定要引起重视，非常的美、精妙！以后的课还会经常见到

题目1.爱吃香蕉的珂珂

题目描述

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。

珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

提示：

1 <= piles.length <= 10^4
piles.length <= h <= 10^9
1 <= piles[i] <= 10^9

测试链接

875.爱吃香蕉的珂珂

思路

估计最终答案可能的范围是什么

最少：一个小时吃 1 根

最多：一个小时吃 piles 最大值根，因为吃更快也没用了，一个小时最多吃一堆

分析问题的答案和给定条件之间的单调性

吃的越快，越容易在警卫回来前吃完

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入吃的速度，返回吃完所有香蕉花的时间

答案

func minEatingSpeed(piles []int, h int) int {
	// if h < len(piles) {
	// 	panic("没有答案")
	// }
	// 答案必定在 [l, r] 中
	l := 1
	r := 0 // max
	for _, num := range piles {
		r = max(r, num)
	}
	ans := 0
	for l <= r {
		m := l + (r-l)>>1
		if f(piles, m) <= h {
			// 达标！记录答案
			ans = m
			r = m - 1
		} else {
			// 不达标
			l = m + 1
		}
	}
	return ans
}
 
// piles: 香蕉重量
// speed: 吃香蕉的速度
// 返回吃完所有的香蕉，耗费的时间
func f(piles []int, speed int) int {
	ans := 0
	for _, num := range piles {
		// a / b 想向上取整，可以写成: (a+b-1) / b
	    // 前提是 a 和 b 都是非负数
		ans += (num + speed - 1) / speed
	}
	return ans
}

复杂度

时间复杂度： $O (n * l o g^{ma x})$ ，f： $O (n)$ ，二分： $O (l o g^{ma x})$
空间复杂度： $O (1)$

题目2.分割数组的最大值(画匠问题)

题目描述

给定一个非负整数数组 nums 和一个整数 k ，你需要将这个数组分成 k 个非空的连续子数组。

设计一个算法使得这 k 个子数组各自和的最大值最小。

测试链接

410.分割数组的最大值

思路

估计最终答案可能的范围是什么

最少：数组最大值，因为子数组要求非空

最多：数组累加和

分析问题的答案和给定条件之间的单调性

分成的子数组越多，每一个子数组的累加和最大值越小

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入每一子数组的累加和要 <= limit，返回需要分成几个子数组

答案

func splitArray(nums []int, k int) int {
	l := 0 // max
	r := 0 // sum
	for _, num := range nums {
		l = max(l, num)
		r += num
	}
	ans := 0
	for l <= r {
		m := l + (r-l)>>1
		if f(nums, m) <= k {
			ans = m
			r = m - 1
		} else {
			l = m + 1
		}
	}
	return ans
}
 
// limit: 每一子数组的累加和要 <= limit
// 返回需要分成几个子数组
func f(nums []int, limit int) int {
	ans := 1
	sum := 0
	for _, num := range nums {
		if num > limit {
			return math.MaxInt // 分不出来
		}
		sum += num
		if sum > limit {
			ans++
			sum = num
		}
	}
	return ans
}

复杂度

时间复杂度： $O (n * l o g^{s u m - ma x})$ ，f： $O (n)$ ，二分： $O (l o g^{s u m - ma x})$
空间复杂度： $O (1)$

题目3.机器人跳跃问题

题目描述

机器人正在玩一个古老的基于 DOS 的游戏。游戏中有 N+1 座建筑——从 0 到 N 编号，从左到右排列。编号为 0 的建筑高度为 0 个单位，编号为 i 的建筑的高度为 H(i)个单位。

起初，机器人在编号为 0 的建筑处。每一步，它跳到下一个（右边）建筑。假设机器人在第 k 个建筑，且它现在的能量值是 E, 下一步它将跳到第个 k+1 建筑。它将会得到或者失去正比于与 H(k+1) 与 E 之差的能量。如果 H(k+1) > E 那么机器人就失去 H(k+1) - E 的能量值，否则它将得到 E - H(k+1) 的能量值。

游戏目标是到达第个 N 建筑，在这个过程中，能量值不能为负数个单位。现在的问题是机器人以多少能量值开始游戏，才可以保证成功完成游戏？

测试链接

机器人跳跃问题

思路

估计最终答案可能的范围是什么

最少初始能量：0，建筑高度都是 0 的情况下

最多初始能量：建筑高度最大值

分析问题的答案和给定条件之间的单调性

初始能量越多（得到的能量多、失去的能量少）越容易到达最后一个建筑

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入初始能量，返回能否到达最后一个建筑

一个坑：能量值增长可能会溢出 int 范围，加一个与最高建筑比较的判断，一可以防止溢出导致答案错误；二可以剪枝，提前返回可以到达最后一个建筑

答案

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 1e5 + 1
)
 
var (
	arr  = [MAXN]int{}
	n    int
	maxx int // 数组最大值
)
 
func main() {
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		maxx = 0
		for i := 0; i < n; i++ {
			in.Scan()
			arr[i], _ = strconv.Atoi(in.Text())
			maxx = max(maxx, arr[i])
		}
		l := 0
		r := maxx
		m := 0
		ans := 0
		for l <= r {
			m = l + (r-l)>>1
			if f(m) {
				ans = m
				r = m - 1
			} else {
				l = m + 1
			}
		}
		fmt.Fprintln(out, ans)
	}
	out.Flush()
}
 
// energy: 初始能量
// 返回能否到达最后一个建筑
func f(energy int) bool {
	for i := 0; i < n; i++ {
		if energy > arr[i] {
			energy += energy - arr[i]
		} else {
			energy -= arr[i] - energy
		}
		// 1. 剪枝: 当前能力比最高建筑都大，必定能到达最后一个建筑
		// 2. 防止能量 int 溢出: 能量一直加，可能溢出 int 范围，导致结果错误
		if energy >= maxx {
			return true
		}
		if energy < 0 {
			return false
		}
	}
	return true
}
 
// 牛客 go 版本太低，没有内置的 max 函数
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

复杂度

时间复杂度： $O (n * l o g^{ma x})$ ，f： $O (n)$ ，二分： $O (l o g^{ma x})$
空间复杂度： $O (1)$

题目4.找出第 K 小的数对距离

题目描述

数对 (a,b) 由整数 a 和 b 组成，其数对距离定义为 a 和 b 的绝对差值。

给你一个整数数组 nums 和一个整数 k ，数对由 nums[i] 和 nums[j] 组成且满足 0 <= i < j < nums.length 。返回 所有数对距离中 第 k 小的数对距离。

示例 1：

输入：nums = [1,3,1], k = 1

输出：0

解释：数对和对应的距离如下：

(1,3) -> 2

(1,1) -> 0

(3,1) -> 2

距离第 1 小的数对是 (1,1)，距离为 0

示例 2：

输入：nums = [1,1,1], k = 2

输出：0

示例 3：

输入：nums = [1,6,1], k = 3

输出：5

提示：

n == nums.length
2 <= n <= 10^4
0 <= nums[i] <= 10^6
1 <= k <= n * (n - 1) / 2

测试链接

719.找出第 K 小的数对距离

思路

估计最终答案可能的范围是什么

最小数对距离：0

最大数对距离：max - min

分析问题的答案和给定条件之间的单调性

数对限制距离越大，能得到更多的数对个数符合 <= 限制距离

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入 arr 中任意两数的差值 <= limit，返回有几个符合要求的数对

答案

func smallestDistancePair(nums []int, k int) int {
	ans := 0
	sort.Ints(nums) // 为了 f 的滑动窗口
	n := len(nums)
	minn := nums[0]
	maxx := nums[n-1]
	l := 0
	r := maxx - minn
	m := 0
	for l <= r {
		m = l + (r-l)>>1
		if f(nums, m) >= k {
			ans = m
			r = m - 1
		} else {
			l = m + 1
		}
	}
	return ans
}
 
// arr 升序排列
// arr 中任意两数的差值 <= limit
// 这样的数字配对，有几对？
func f(arr []int, limit int) int {
	n := len(arr)
	ans := 0
	// 滑动窗口，收集以 l 开头的答案
	r := 1
	for l := 0; l < n; l++ {
		for r != n && arr[r]-arr[l] <= limit {
			r++
		}
		ans += r - l - 1
	}
	return ans
}

复杂度

时间复杂度： $O (n * l o g^{n} + n * l o g^{ma x - min})$ ，排序： $O (n * l o g^{n})$ ，f（滑动窗口）： $O (n)$ ，二分： $O (l o g^{ma x - min})$
空间复杂度： $O (1)$

题目5.同时运行 N 台电脑的最长时间

题目描述

你有 n 台电脑。给你整数 n 和一个下标从 0 开始的整数数组 batteries ，其中第 i 个电池可以让一台电脑运行 batteries[i] 分钟。你想使用这些电池让全部 n 台电脑同时运行。

一开始，你可以给每台电脑连接 至多一个电池 。然后在任意整数时刻，你都可以将一台电脑与它的电池断开连接，并连接另一个电池，你可以进行这个操作 任意次 。新连接的电池可以是一个全新的电池，也可以是别的电脑用过的电池。断开连接和连接新的电池不会花费任何时间。

注意，你不能给电池充电。

请你返回你可以让 n 台电脑同时运行的最长分钟数。

示例 1：

输入：n = 2, batteries = [3,3,3]

输出：4

解释：

一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 1 连接。

2 分钟后，将第二台电脑与电池 1 断开连接，并连接电池 2 。注意，电池 0 还可以供电 1 分钟。

在第 3 分钟结尾，你需要将第一台电脑与电池 0 断开连接，然后连接电池 1 。

在第 4 分钟结尾，电池 1 也被耗尽，第一台电脑无法继续运行。

我们最多能同时让两台电脑同时运行 4 分钟，所以我们返回 4 。

示例 2：

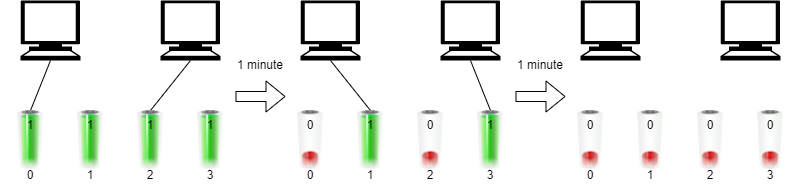
输入：n = 2, batteries = [1,1,1,1]

输出：2

解释：

一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 2 连接。

一分钟后，电池 0 和电池 2 同时耗尽，所以你需要将它们断开连接，并将电池 1 和第一台电脑连接，电池 3 和第二台电脑连接。

1 分钟后，电池 1 和电池 3 也耗尽了，所以两台电脑都无法继续运行。

我们最多能让两台电脑同时运行 2 分钟，所以我们返回 2 。

提示：

1 <= n <= batteries.length <= 10^5
1 <= batteries[i] <= 10^9

测试链接

2141.同时运行 N 台电脑的最长时间

思路

估计最终答案可能的范围是什么

最短运行时间：0

最长运行时间：sum，电脑只有 1 台时

分析问题的答案和给定条件之间的单调性

让电脑共同运行时间越短，越容易做到

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入一个运行时间，返回能不能做到

答案

func maxRunTime(n int, batteries []int) int64 {
	ans := 0
	l := 0
	r := 0 // sum
	m := 0
	for _, num := range batteries {
		r += num
	}
 
	for l <= r {
		m = l + (r-l)>>1
		if f(batteries, n, m) {
			ans = m
			l = m + 1
		} else {
			r = m - 1
		}
	}
	return int64(ans)
}
 
// 让 n 台电脑共同运行 time 分钟，能不能做到
func f(arr []int, n, time int) bool {
	// 碎片电量总和
	sum := 0
	for _, num := range arr {
		if num > time {
			// 一个电池搞定一个电脑（一直在给该电脑供电）
			n--
		} else {
			// 是碎片电池
			sum += num
		}
		// 碎片电量够供满，“碎片拼接”
		if sum >= n*time {
			return true
		}
	}
	return false
}

贪心优化：

func maxRunTime(n int, batteries []int) int64 {
	maxx := 0
	sum := 0
	for _, num := range batteries {
		maxx = max(maxx, num)
		sum += num
	}
	if sum > maxx*n {
		// sum > maxx * n
		// 说明最终的供电时间一定在 >= maxx，而如果最终的供电时间 >= maxx
		// 则：对于最终的答案 X 来说，所有电池都是"碎片拼接"的概念
		// 那么寻找 X * num <= sum 的情况中，尽量大的 X 即可
		// 即：sum / n
		return int64(sum / n)
	}
 
	// 最终的供电时间一定在 <maxx 范围上
	// [0, sum] 二分范围，可能定的比较粗，虽然不影响，但毕竟是有点慢
	// [0, maxx] 二分范围！更精细的范围，二分次数会变少
	ans := 0
	l := 0
	r := maxx
	m := 0
	for l <= r {
		m = l + (r-l)>>1
		if f(batteries, n, m) {
			ans = m
			l = m + 1
		} else {
			r = m - 1
		}
	}
	return int64(ans)
}
 
// 让 n 台电脑共同运行 time 分钟，能不能做到
func f(arr []int, n, time int) bool {
	// 碎片电量总和
	sum := 0
	for _, num := range arr {
		if num > time {
			// 一个电池搞定一个电脑（一直在给该电脑供电）
			n--
		} else {
			// 是碎片电池
			sum += num
		}
		// 碎片电量够供满
		if sum >= n*time {
			return true
		}
	}
	return false
}

复杂度

二分答案法：

时间复杂度： $O (n * l o g^{s u m})$ ，f： $O (n)$ ，二分： $O (l o g^{s u m})$
空间复杂度： $O (1)$

二分答案法 + 贪心：

时间复杂度： $O (n * l o g^{ma x})$ ，f： $O (n)$ ，二分： $O (l o g^{ma x})$
空间复杂度： $O (1)$

题目6.计算等位时间

谷歌的面试，这个题连考了 2 个月

找不到测试链接，所以用对数器验证

题目描述

给定一个数组 arr 长度为 n，表示 n 个服务员，每服务一个客人的时间（正数）

给定一个非负数 m，表示有 m 个人等位，如果你是刚来的人，每个客人都遵循有空位就上的原则，请问你需要等多久？

假设 m 远远大于 n，比如 0 < n <= 10^3，0 <= m <= 10^9，该怎么做是最优解？

题目分析

每个客人都遵循有空位就上的原则，不管他们选择哪个服务员，你被服务的时间一定是确定的，不可能因为之前的客人选择的服务员不同，而导致你的服务时间发生变化

思路

估计最终答案可能的范围是什么

最早服务时间：0，前面排的客人少于服务员

最晚服务时间：min * m，让服务最快的一个服务员服务所有客人

分析问题的答案和给定条件之间的单调性

服务员工作时间越长，服务的客人越多

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入工作时间，返回可以服务几位客人（结束的、开始的客人都算）

答案

package main
 
import (
	"container/heap"
	"fmt"
	"math"
	"math/rand"
)
 
// 堆模拟
func waitingTime1(arr []int, m int) int {
	// [2]int: [醒来时间，服务一个客人要多久]
	minHeap := NewMinHeap(len(arr))
	for _, num := range arr {
		heap.Push(&minHeap, [2]int{0, num})
	}
	for i := 0; i < m; i++ {
		cur := heap.Pop(&minHeap).([2]int)
		cur[0] += cur[1]
		heap.Push(&minHeap, cur)
	}
	return heap.Pop(&minHeap).([2]int)[0]
}
 
type MinHeap [][2]int
 
func NewMinHeap(capacity int) MinHeap {
	return make(MinHeap, 0, capacity)
}
 
func (h MinHeap) Len() int {
	return len(h)
}
 
func (h MinHeap) Less(i, j int) bool {
	return h[i][0] < h[j][0]
}
 
func (h MinHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}
 
func (h *MinHeap) Push(x any) {
	(*h) = append(*h, x.([2]int))
}
 
func (h *MinHeap) Pop() any {
	length := h.Len()
	ans := (*h)[length-1]
	(*h) = (*h)[:length-1]
	return ans
}
 
// 二分答案法
func waitingTime2(arr []int, m int) int {
	minn := math.MaxInt
	for _, num := range arr {
		minn = min(minn, num)
	}
	ans := 0
	l := 0
	r := minn * m
	mid := 0
	for l <= r {
		mid = l + (r-l)>>1
		if f(arr, mid) >= m+1 {
			ans = mid
			r = mid - 1
		} else {
			l = mid + 1
		}
	}
	return ans
}
 
// 如果每个服务员工作 time，可以接待几位客人（结束的、开始的客人都算）
func f(arr []int, time int) int {
	ans := 0
	for _, num := range arr {
		// 开始接受服务时间，所以要 +1
		ans += (time / num) + 1
	}
	return ans
}
 
const (
	N          = 50
	V          = 30
	M          = 3000
	TEST_TIMES = 20000
)
 
func main() {
	for i := 0; i < TEST_TIMES; i++ {
		arr := generateArray()
		m := rand.Intn(M)
		ans1 := waitingTime1(arr, m)
		ans2 := waitingTime2(arr, m)
		if ans1 != ans2 {
			panic("error")
		}
	}
	fmt.Println("success")
}
 
func generateArray() []int {
	n := rand.Intn(N) + 1
	arr := make([]int, n)
	for i := range arr {
		arr[i] = rand.Intn(V) + 1
	}
	return arr
}

复杂度

堆模拟：

时间复杂度： $O (m * l o g^{n})$
空间复杂度： $O (n)$

二分答案法：

时间复杂度： $O (n * l o g^{min * m})$
空间复杂度： $O (1)$

因为题目数据量给定 m 远远大于 n，所以二分答案法是最优解

题目7.刀砍毒杀怪兽问题

本题来自真实大厂笔试，找不到测试链接，所以用对数器验证

题目描述

怪兽的初始血量是一个整数 hp，给出每一回合刀砍和毒杀的数值 cuts 和 poisons

两个数组 cuts、poisons，长度都是 n，代表你一共可以进行 n 回合

每一回合你只能选择刀砍或者毒杀中的一个动作

第 i 回合如果用刀砍，怪兽在这回合会直接损失 cuts[i] 的血，不再有后续效果
第 i 回合如果用毒杀，怪兽在这回合不会损失血量，但是之后每回合都损失 poisons[i] 的血量，并且你选择的所有毒杀效果，在之后的回合都会叠加

如果你在 n 个回合内没有直接杀死怪兽，意味着你已经无法有新的行动了，但是怪兽如果有中毒效果的话，那么怪兽依然会在血量耗尽的那回合死掉

返回至少多少回合，怪兽会死掉

数据范围：

1 <= n <= 10^5
1 <= hp <= 10^9
1 <= cuts[i]、poisons[i] <= 10^9

思路

估计最终答案可能的范围是什么

最少回合数：1，一刀砍死

最多回合数：hp+1，第一回合用毒杀，最多 hp+1 回合就会被毒死

分析问题的答案和给定条件之间的单调性

回合数越多，怪兽被打死的可能性越大

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入限制最多几个回合打死怪兽，返回是否能做到

答案

package main
 
import (
	"fmt"
	"math"
	"math/rand"
)
 
var (
	n       int   // 回合数，cuts、poisons 的长度
	cuts    []int // 每一回合刀砍的效果
	poisons []int // 每一回合毒杀的效果
	hp      int   // 怪兽血量
)
 
// 三维动态规划
func fast1() int {
	sum := 0
	for _, poison := range poisons {
		sum += poison
	}
	// dp[round][curHp][poison]:
	// 第 round - 1 回合
	// 累计毒杀伤害 poison
	// 怪兽血量还剩 curHp
	// 的答案
	dp := make([][][]int, n)
	for i := range dp {
		dp[i] = make([][]int, sum+1)
		for j := range dp[i] {
			dp[i][j] = make([]int, hp+1)
		}
	}
	return process(0, 0, hp, dp)
}
 
// round: 当前回合数 - 1
// poison: 累计的毒杀伤害
// curHp: 当前怪兽血量
func process(round, poison, curHp int, dp [][][]int) int {
	curHp -= poison
	if curHp <= 0 { // 杀死怪兽
		return round + 1
	}
	if round == n { // 没有新行动了
		if poison == 0 {
			return math.MaxInt // 打不死
		} else {
			// 剩余血量被毒杀，向上取整
			return n + 1 + (curHp+poison-1)/poison
		}
	}
	if dp[round][poison][curHp] != 0 {
		// 记忆化搜索
		return dp[round][poison][curHp]
	}
	// 选择刀砍
	p1 := round + 1
	if curHp > cuts[round] {
		p1 = process(round+1, poison, curHp-cuts[round], dp)
	}
	// 选择毒杀
	p2 := process(round+1, poison+poisons[round], curHp, dp)
	ans := min(p1, p2)
	dp[round][poison][curHp] = ans
	return ans
}
 
// 二分答案法
func fast2() int {
	ans := math.MaxInt
	l := 1
	r := hp + 1
	m := 0
	for l <= r {
		m = l + (r-l)>>1
		if f(m) {
			ans = m
			r = m - 1
		} else {
			l = m + 1
		}
	}
	return ans
}
 
// limit: 回合的限制
func f(limit int) bool {
	round := min(n, limit)
	curHp := hp
	for i := 0; i < round; i++ {
		curHp -= max(cuts[i], poisons[i]*(limit-i-1))
		if curHp <= 0 {
			return true
		}
	}
	return false
}
 
const (
	N          = 30
	V          = 20
	H          = 300
	TEST_TIMES = 10000
)
 
func main() {
	for i := 0; i < TEST_TIMES; i++ {
		n = rand.Intn(N) + 1
		cuts = generateArray(n)
		poisons = generateArray(n)
		hp = rand.Intn(H) + 1
		ans1 := fast1()
		ans2 := fast2()
		if ans1 != ans2 {
			panic("error")
		}
	}
	fmt.Println("success")
}
 
func generateArray(n int) []int {
	arr := make([]int, n)
	for i := range arr {
		arr[i] = rand.Intn(V) + 1
	}
	return arr
}

复杂度

三维动态规划：

时间复杂度：#todo
空间复杂度： $O (n * h p * s u m (p o i so n s))$

二分答案法：

时间复杂度： $O (n * l o g^{h p})$
空间复杂度： $O (1)$

题目8.工厂生产糖果问题

题目描述

工厂可以生产 n 种糖果，工厂每天生产 i 号糖果的数量为 arr[i]，不同编号的糖果并行生产

工厂接到一个订单，要求是 a 包糖果、每包糖果必须是同一种类、每包的数量不能少于 b 个，一种糖果可以生产很多包

返回至少需要多少天才能完成订单

思路

估计最终答案可能的范围是什么

最少天数：1

最多天数：a*b/max 向上取整，让生产最快的糖果达到要求

分析问题的答案和给定条件之间的单调性

天数越多，生产的糖果越多，越容易达到订单要求

建立一个 f 函数，当答案固定的情况下，判断给定的条件是否达标

输入生产天数，返回能生产多少包糖果

答案

package main
 
import (
	"fmt"
	"math/rand"
)
 
var (
	arr []int // 工厂每天生产 i号糖果的数量为 arr[i]
	n   int   // len(arr)
	a   int   // 要求 a 包糖果
	b   int   // 每包的数量不能少于 b 个
)
 
// 普通方法
func day1() int {
	day := 0               // 天数
	count := 0             // 已经生产了几包糖果
	rest := make([]int, n) // 不够一包的糖果数
	for count < a {
		for i, v := range arr {
			rest[i] += v
			for rest[i] >= b {
				count++
				rest[i] -= b
			}
		}
		day++
	}
	return day
}
 
// 二分答案法
func day2() int {
	maxx := 0
	for _, num := range arr {
		maxx = max(maxx, num)
	}
	day := 0
	l := 1
	r := (a*b + maxx - 1) / maxx
	m := 0
	for l <= r {
		m = l + (r-l)>>1
		if f(m) >= a {
			day = m
			r = m - 1
		} else {
			l = m + 1
		}
	}
	return day
}
 
// day 天，能做几包糖果？
func f(day int) int {
	ans := 0
	for _, num := range arr {
		ans += num * day / b
	}
	return ans
}
 
const (
	N          = 10
	V          = 10
	A          = 200
	B          = 50
	TEST_TIMES = 10000
)
 
func main() {
	for i := 0; i < TEST_TIMES; i++ {
		n = rand.Intn(N) + 1
		arr = generateArray(n)
		a = rand.Intn(A) + 1
		b = rand.Intn(B) + 1
		ans1 := day1()
		ans2 := day2()
		// fmt.Println(arr, a, b, ans1, ans2)
		if ans1 != ans2 {
			panic("error")
		}
	}
	fmt.Println("success")
}
 
func generateArray(n int) []int {
	arr := make([]int, n)
	for i := range arr {
		arr[i] = rand.Intn(V) + 1
	}
	return arr
}

复杂度

普通方法：

时间复杂度： $O (n * (a * b / s u m))$
空间复杂度： $O (n)$

二分答案法：

时间复杂度： $O (n * l o g^{a * b / ma x})$
空间复杂度： $O (1)$

My-Notes

Explorer

033.二分答案法与相关题目

二分答案法 §

题目1.爱吃香蕉的珂珂 §

题目描述 §

测试链接 §

思路 §

答案 §

复杂度 §

题目2.分割数组的最大值(画匠问题) §

题目描述 §

测试链接 §

思路 §

答案 §

复杂度 §

题目3.机器人跳跃问题 §

题目描述 §

测试链接 §

思路 §

答案 §

复杂度 §

题目4.找出第 K 小的数对距离 §

题目描述 §

测试链接 §

思路 §

答案 §

复杂度 §

题目5.同时运行 N 台电脑的最长时间 §

题目描述 §

测试链接 §

思路 §

答案 §

复杂度 §

题目6.计算等位时间 §

题目描述 §

题目分析 §

思路 §

答案 §

复杂度 §

题目7.刀砍毒杀怪兽问题 §

题目描述 §

思路 §

答案 §

复杂度 §

题目8.工厂生产糖果问题 §

题目描述 §

思路 §

答案 §

复杂度 §

Graph View

Table of Contents

Backlinks

二分答案法

题目1.爱吃香蕉的珂珂

题目描述

测试链接

思路

答案

复杂度

题目2.分割数组的最大值(画匠问题)

题目描述

测试链接

思路

答案

复杂度

题目3.机器人跳跃问题

题目描述

测试链接

思路

答案

复杂度

题目4.找出第 K 小的数对距离

题目描述

测试链接

思路

答案

复杂度

题目5.同时运行 N 台电脑的最长时间

题目描述

测试链接

思路

答案

复杂度

题目6.计算等位时间

题目描述

题目分析

思路

答案

复杂度

题目7.刀砍毒杀怪兽问题

题目描述

思路

答案

复杂度

题目8.工厂生产糖果问题

题目描述

思路

答案

复杂度