My-Notes

060.树型dp-上

19分钟阅读

前置知识：讲解017、讲解018、讲解036、讲解037 二叉树基础内容、建图、链式前向星建图、拓扑排序、拓扑排序的扩展技巧（讲的题就是有向无环图上做动态规划）

树型 dp

本节课讲述最常见的树型 dp 问题，详解树型 dp 的解题套路

下节课会讲述树型 dp 利用 dfn 序的内容

树是一种有向无环图

头节点没有父亲，其他节点只有一个父亲的有向无环图，直观理解为发散状

在树上，从头节点出发到任何节点的路径是唯一的，不管二叉树还是多叉树都如此

树型 dp 在树上做动态规划，依赖关系比一般动态规划简单，因为绝大部分多数都是父依赖子

注意：只是依赖关系简单，不代表题目简单

树型 dp 套路

  1. 分析父树得到答案需要子树的哪些信息
  2. 把子树信息的全集定义成递归返回值
  3. 通过递归让子树返回全集信息
  4. 整合子树的全集信息得到父树的全集信息并返回

备注

拓扑排序的扩展技巧 讲的是 DAG（Directed Acyclic Graph，有向无环图）上做动态规划，不要跳过

树型 dp 中有关换根 dp 的内容，将放在【扩展】课程阶段讲述

题目1.最大 BST 子树

题目描述

给定一个二叉树，找到其中最大的二叉搜索树（BST）子树，并返回该子树的大小

其中，最大指的是子树节点数最多的

二叉搜索树（BST）中的所有节点都具备以下属性：

  • 左子树的值小于其父（根）节点的值
  • 右子树的值大于其父（根）节点的值

注意：子树必须包含其所有后代

测试链接

333.最大 BST 子树

思路

分析父树得到答案需要子树的哪些信息？

  1. 整棵树中最大的 BST 子树的节点个数，即：题目要求返回值
  2. 整棵树是否是 BST：为 1 服务
  3. 整棵树的最大值和最小值：为判断 2 服务

整合子树的全集信息得到父树的全集信息：

  1. 整棵树的最大值：左子树最大值、右子树最大值、当前头节点值，三者取最大
  2. 整棵树的最小值：左子树最小值、右子树最小值、当前头节点值，三者取最小
  3. 整棵树是否是 BST：左子树和右子树都是 BST，并且左子树最大值 < 当前头节点值 < 右子树最小值
  4. 整棵树中最大的 BST 子树的节点个数：
    1. 整棵树是 BST：左子树节点个数 + 右子树节点个数 + 当前头节点（1）
    2. 整棵树不是 BST：左子树中最大的 BST 子树、右子树中最大的 BST 子树，二者取较大值

答案

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}
 
type Info struct {
	Max        int  // 整棵树的最大值
	Min        int  // 整棵树的最小值
	IsBST      bool // 整棵树是否是 BST
	MaxBSTSize int  // 整棵树中最大的 BST 子树的节点个数
}
 
func largestBSTSubtree(root *TreeNode) int {
	return f(root).MaxBSTSize
}
 
func f(node *TreeNode) Info {
	if node == nil {
		return Info{math.MinInt, math.MaxInt, true, 0}
	}
	lInfo := f(node.Left)
	rInfo := f(node.Right)
	// 左 4 个信息和右 4 个信息整合出 node 的 4 个信息并返回
	maxx := max(node.Val, lInfo.Max, rInfo.Max)
	minn := min(node.Val, lInfo.Min, rInfo.Min)
	isBST := lInfo.IsBST && rInfo.IsBST && lInfo.Max < node.Val && node.Val < rInfo.Min
	maxBSTSize := 0
	if isBST {
		maxBSTSize = lInfo.MaxBSTSize + rInfo.MaxBSTSize + 1
	} else {
		maxBSTSize = max(lInfo.MaxBSTSize, rInfo.MaxBSTSize)
	}
	return Info{maxx, minn, isBST, maxBSTSize}
}

复杂度

  • 时间复杂度：， 为二叉树节点个数
    • 整个过程是后序遍历
    • 信息整合是
  • 空间复杂度：， 为二叉树高度
    • 递归栈空间

题目2.二叉搜索子树的最大键值和

题目描述

给你一棵以 root 为根的 二叉树 ，请你返回 任意 二叉搜索子树的最大键值和。

键值和即累加和

二叉搜索树的定义如下：

  • 任意节点的左子树中的键值都 小于 此节点的键值。
  • 任意节点的右子树中的键值都 大于 此节点的键值。
  • 任意节点的左子树和右子树都是二叉搜索树。

提示：

  • 每棵树有 1 到 40000 个节点。
  • 每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。

测试链接

1373.二叉搜索子树的最大键值和

答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
type Info struct {
	Max       int
	Min       int
	IsBST     bool
	Sum       int // 当前树累加和
	MaxBSTSum int // 最大 BST 子树累加和
}
 
func maxSumBST(root *TreeNode) int {
	return f(root).MaxBSTSum
}
 
func f(node *TreeNode) Info {
	if node == nil {
		return Info{math.MinInt, math.MaxInt, true, 0, 0}
	}
	lInfo := f(node.Left)
	rInfo := f(node.Right)
	maxx := max(lInfo.Max, rInfo.Max, node.Val)
	minn := min(lInfo.Min, rInfo.Min, node.Val)
	isBST := lInfo.IsBST && rInfo.IsBST && lInfo.Max < node.Val && node.Val < rInfo.Min
	sum := lInfo.Sum + rInfo.Sum + node.Val
	maxBSTSum := max(lInfo.MaxBSTSum, rInfo.MaxBSTSum)
	if isBST {
		maxBSTSum = max(maxBSTSum, sum)
	}
	return Info{maxx, minn, isBST, sum, maxBSTSum}
}

题目3.二叉树的直径

题目描述

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

提示：

  • 树中节点数目在范围 [1, 10^4] 内
  • -100 <= Node.val <= 100

测试链接

543.二叉树的直径

思路

  1. 不经过根节点：左子树直径和右子树直径的较大值
  2. 经过根节点：左树高度 + 右树高度

答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
type Info struct {
	Height   int // 高度
	Diameter int // 直径
}
 
func diameterOfBinaryTree(root *TreeNode) int {
	return f(root).Diameter
}
 
func f(node *TreeNode) Info {
	if node == nil {
		return Info{0, 0}
	}
	lInfo := f(node.Left)
	rInfo := f(node.Right)
	height := max(lInfo.Height, rInfo.Height) + 1
	diameter := max(lInfo.Diameter, rInfo.Diameter, lInfo.Height+rInfo.Height)
	return Info{height, diameter}
}

题目4.在二叉树中分配硬币

题目描述

给你一个有 n 个结点的二叉树的根结点 root ，其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点，或者从子结点移动到父结点。

返回使每个结点上 只有 一枚硬币所需的 最少 移动次数。

示例 1：

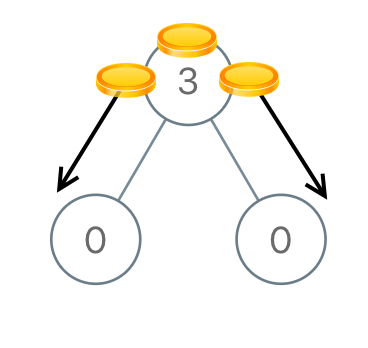
输入：root = [3,0,0]

输出：2

解释：一枚硬币从根结点移动到左子结点，一枚硬币从根结点移动到右子结点。

示例 2：

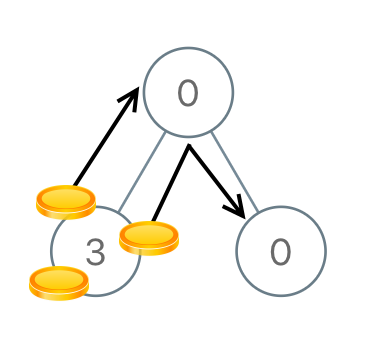
输入：root = [0,3,0]

输出：3

解释：将两枚硬币从根结点的左子结点移动到根结点（两次移动）。然后，将一枚硬币从根结点移动到右子结点。

提示：

  • 树中节点的数目为 n
  • 1 <= n <= 100
  • 0 <= Node.val <= n
  • 所有 Node.val 的值之和是 n

测试链接

979.在二叉树中分配硬币

思路

左子树多出来的硬币肯定要移动到根节点，再从根节点移动到右子树

答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
type Info struct {
	NodeCnt int // 节点数
	Val     int // 每个节点的硬币总和
	MoveCnt int // 移动的步数
}
 
func distributeCoins(root *TreeNode) int {
	return f(root).MoveCnt
}
 
func f(node *TreeNode) Info {
	if node == nil {
		return Info{0, 0, 0}
	}
	lInfo := f(node.Left)
	rInfo := f(node.Right)
	nodeCnt := lInfo.NodeCnt + rInfo.NodeCnt + 1
	val := lInfo.Val + rInfo.Val + node.Val
	// 左子树内部移动的次数 + 右子树内部移动的次数 + 跨左右要经过当前根节点移动的次数
	moveCnt := lInfo.MoveCnt + rInfo.MoveCnt + abs(lInfo.NodeCnt-lInfo.Val) + abs(rInfo.NodeCnt-rInfo.Val)
	return Info{nodeCnt, val, moveCnt}
}
 
func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

题目5.没有上司的舞会

与 二叉树打家劫舍问题 问题类似，区别在于打家劫舍是二叉树，本题是多叉树

题目描述

某大学有 n 个职员，编号为 1~n。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 ri​，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

提示：

  • 1 ≤ n ≤ 6×10^3
  • −128 ≤ ri ​≤ 127
  • 给出的关系一定是一棵树

测试链接

P1352 没有上司的舞会

答案

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 6001
)
 
var (
	n     int
	happy = [MAXN]int{}  // 快乐值
	boss  = [MAXN]bool{} // 谁是校长
 
	// 动态规划表
	// no[i]：i 为头的整棵树，在 i 不来的情况下，整棵树能得到的最大快乐值
	no = [MAXN]int{}
	// yes[i]：i 为头的整棵树，在 i 来的情况下，整棵树能得到的最大快乐值
	yes = [MAXN]int{}
 
	// 链式前向星建图
	head = [MAXN]int{}
	next = [MAXN]int{}
	to   = [MAXN]int{}
	cnt  = 1
)
 
func main() {
	// s := `7
	// 1
	// 1
	// 1
	// 1
	// 1
	// 1
	// 1
	// 1 3
	// 2 3
	// 6 4
	// 7 4
	// 4 5
	// 3 5`
	// in := bufio.NewScanner(strings.NewReader(s))
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		build()
		for i := 1; i <= n; i++ {
			in.Scan()
			happy[i], _ = strconv.Atoi(in.Text())
		}
		low, high := 0, 0
		for i := 1; i < n; i++ {
			in.Scan()
			low, _ = strconv.Atoi(in.Text())
			in.Scan()
			high, _ = strconv.Atoi(in.Text())
			addEdge(high, low)
			boss[low] = false
		}
		root := 0
		for i := 1; i <= n; i++ {
			if boss[i] {
				root = i
				break
			}
		}
		f(root)
		fmt.Fprintln(out, max(yes[root], no[root]))
	}
	out.Flush()
}
 
func f(node int) {
	no[node] = 0
	yes[node] = happy[node]
	low := 0
	for i := head[node]; i > 0; i = next[i] {
		low = to[i]
		// 把 yes[low] 和 no[low] 都填充好
		f(low)
		// node 不来，其下级 low 可以来也可以不来
		no[node] += max(no[low], yes[low])
		// node 来，其下级 low 必须不来
		yes[node] += no[low]
	}
}
 
func build() {
	cnt = 1
	for i := 1; i <= n; i++ {
		boss[i] = true
		head[i] = 0
	}
}
 
func addEdge(f, t int) {
	next[cnt] = head[f]
	to[cnt] = t
	head[f] = cnt
	cnt++
}

题目6.监控二叉树

题目描述

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

提示：

  1. 给定树的节点数的范围是 [1, 1000]。
  2. 每个节点的值都是 0。

测试链接

968.监控二叉树

思路

贪心策略：一个相机尽可能多的监控节点

答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
// 遍历过程中会安装摄像头，即：ans++
var ans int
 
func minCameraCover(root *TreeNode) int {
	ans = 0
	// root 节点无覆盖，下方的节点都已经被覆盖，就要在 root 上再放一个摄像头
	if f(root) == 0 {
		ans++
	}
	return ans
}
 
// 假设 x 上方一定有父亲的情况下，这个假设很重要
// x 为头的整棵树，最终想都覆盖，并且想使用最少的摄像头，x 应该是什么样的状态
// 返回值含义：
// 0：x 是无覆盖的状态，x 下方的节点都已经被覆盖
// 1：x 是覆盖状态，x 上没摄像头，x 下方的节点都已经被覆盖
// 2：x 是覆盖状态，x 上有摄像头，x 下方的节点都已经被覆盖
func f(x *TreeNode) byte {
	if x == nil {
		// nil 不需要被覆盖，也无法安装摄像头
		// 就相当于覆盖状态且没摄像头
		return 1
	}
	left := f(x.Left)
	right := f(x.Right)
	// 左节点或右节点只要一个无覆盖，当前节点就需要安装摄像头
	if left == 0 || right == 0 {
		ans++
		return 2
	}
	// 左右节点都被覆盖了，但都没有摄像头，当前节点就覆盖不到了
	if left == 1 && right == 1 {
		return 0
	}
	// 其他情况是左右节点至少有一个有摄像头
	return 1
}

题目7.路径总和 III

题目描述

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

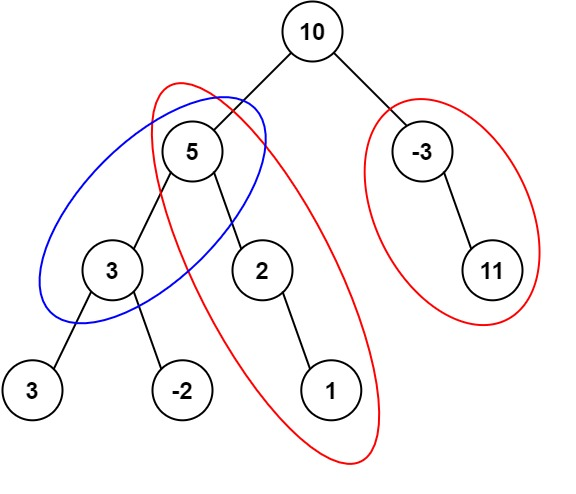
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8

输出：3

解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22

输出：3

提示：

  • 二叉树的节点个数的范围是 [0,1000]
  • -10^9 <= Node.val <= 10^9 
  • -1000 <= targetSum <= 1000

测试链接

437.路径总和 III

思路

之前的题都是父节点向子节点要信息，这道题是子节点向父节点要信息

子节点向父节点要信息：从上方节点走到当前节点，有多少条路径的路径和等于 targetSum

怎么算？记录累加和路径个数，当前前缀和 - 之前某个路径的累加和 == targetSum 就是路径以当前节点作为结尾，路径累加和是 targetSum 的路径数量

答案

路径总和 III

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
var (
	ans    int
	target int
	preSum = map[int]int{}
)
 
func pathSum(root *TreeNode, targetSum int) int {
	ans = 0
	target = targetSum
	// key: 从上方节点走到当前节点的累加和
	// val: 这个累加和出现的次数
	clear(preSum)
	// 默认所有节点都不选的情况下，累加和是 0，就已经出现了 1 次
	preSum[0] = 1
 
	f(root, 0)
 
	return ans
}
 
// 路径必须以 node 作为结尾，路径累加和是 targetSum 的路径数量，累加到全局变量 ans 上
// curSum: 从头节点出发，来到当前节点的时候，累加和是多少
func f(node *TreeNode, curSum int) {
	if node == nil {
		return
	}
	curSum += node.Val
	// 当前累加和 - 之前累加和 == target
	// 就是路径必须以 node 作为结尾，路径累加和是 targetSum 的路径数量
	ans += preSum[curSum-target]
	// 将要处理子节点，将当前节点的 preSum 填好
	preSum[curSum]++
	f(node.Left, curSum)
	f(node.Right, curSum)
	// 回溯：将要返回到父节点，将当前节点的影响取消掉
	preSum[curSum]--
}

反向链接

关系图谱