前置知识：讲解017、讲解018、讲解036、讲解037 二叉树基础内容、建图、链式前向星建图、拓扑排序、拓扑排序的扩展技巧（讲的题就是有向无环图上做动态规划）、01 背包（题目5 需要）

上节课讲述了几个常见的树型 dp 问题，熟悉了树型 dp 的解题套路

本节课见识更多树型 dp 问题（题目1、题目2）

dfn 序

用深度优先遍历的方式遍历整棵树，给每个节点依次标记序号，编号从小到大的顺序就是 dfn 序

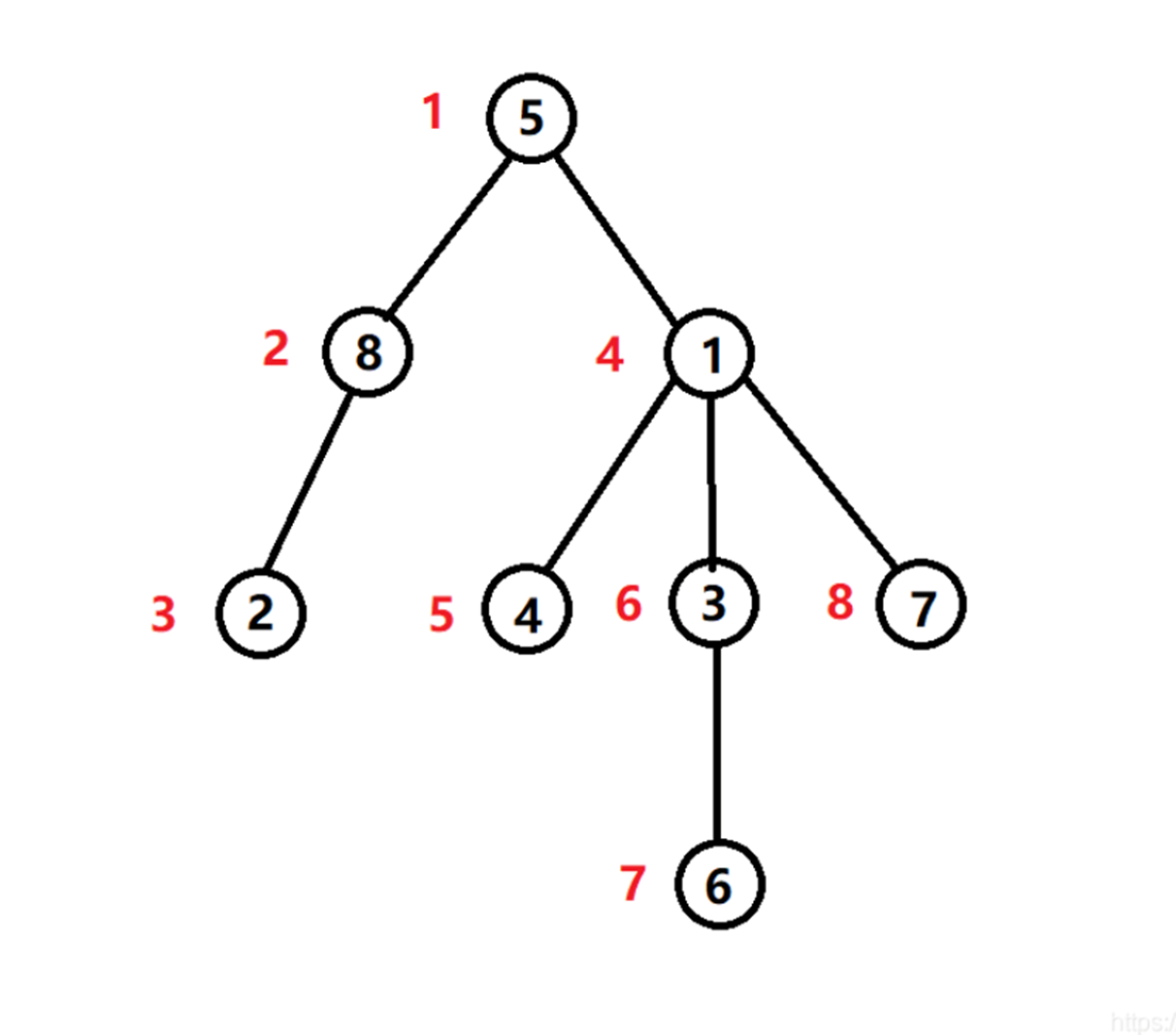
一个子树的序号是连续的，子节点的序号一定比父节点大

dfn 序 + 每颗子树的大小，可以起到定位子树节点的作用

如果某个节点的 dfn 序号是 x，以这个节点为头的子树大小为 y

那么可知，dfn 序号从 x ~ x+y-1 所代表的节点，都属于这个节点的子树

利用这个性质，节点间的关系判断（题目3、题目4），跨子树的讨论（题目5）就会变得方便

备注

dfn 序除了和树型 dp 相关，后续还和很多算法数据结构有关（树链剖分等）

后续内容会在【扩展】、【挺难】课程里安排讲述

题目1.到达首都的最少油耗

题目描述

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] ，表示城市 ai 和 bi 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

提示：

1 <= n <= 10^5
roads.length == n - 1
roads[i].length == 2
0 <= ai, bi < n
ai != bi
roads 表示一棵合法的树。
1 <= seats <= 10^5

测试链接

2477.到达首都的最少油耗

思路

题目输入双向图，无法确定哪个是父哪个是子，所以双向都存

递归要从树根到树叶，从父到子，所以要传父节点防止从子再递归回到父

答案

var (
	graph    [][]int // 图：邻接表
	size     []int   // size[i]：i 子树的节点数
	cost     []int64 // cost[i]：i 子树的人都开车来到 i 节点，消耗多少汽油
	theSeats int
)
 
func minimumFuelCost(roads [][]int, seats int) int64 {
	theSeats = seats
	// 路条数 + 1 就是城市数
	n := len(roads) + 1
	graph = make([][]int, n)
	for i := range graph {
		graph[i] = []int{}
	}
	for _, r := range roads {
		graph[r[0]] = append(graph[r[0]], r[1])
		graph[r[1]] = append(graph[r[1]], r[0])
	}
	size = make([]int, n)
	cost = make([]int64, n)
	f(0, -1)
	return cost[0]
}
 
// 根据图，当前来到 cur 节点，cur 的父节点是 parent
// 遍历完成后，填好 size[cur]、cost[cur]
func f(cur, parent int) {
	size[cur] = 1
	for _, child := range graph[cur] {
		if child == parent {
			// 防止从子再递归回到父
			continue
		}
		// 让子树填好 size[cur]、cost[cur]
		f(child, cur)
		size[cur] += size[child]
		// child 子树汇聚到 child 代价
		cost[cur] += cost[child]
		// 汇聚到 child 的人开车到 cur 代价
		// a/b 向上取整，可以写成 (a+b-1)/b
		cost[cur] += int64((size[child] + theSeats - 1) / theSeats)
	}
}

题目2.相邻字符不同的最长路径

题目描述

给你一棵树（即一个连通、无向、无环图），根节点是节点 0 ，这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树，其中 parent[i] 是节点 i 的父节点，由于节点 0 是根节点，所以 parent[0] == -1 。

另给你一个字符串 s ，长度也是 n ，其中 s[i] 表示分配给节点 i 的字符。

请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ，并返回该路径的长度。

示例 1：

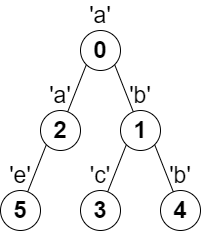
输入：parent = [-1,0,0,1,1,2], s = "abacbe"

输出：3

解释：任意一对相邻节点字符都不同的最长路径是：0 -> 1 -> 3。该路径的长度是 3

可以证明不存在满足上述条件且比 3 更长的路径。

示例 2：

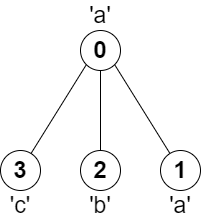
输入：parent = [-1,0,0,0], s = "aabc"

输出：3

解释：任意一对相邻节点字符都不同的最长路径是：2 -> 0 -> 3。该路径的长度为 3

提示：

n == parent.length == s.length
1 <= n <= 10^5
对所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
parent[0] == -1
parent 表示一棵有效的树
s 仅由小写英文字母组成

测试链接

2246.相邻字符不同的最长路径

答案

type Info struct {
	MaxPathFromHead int // 一定要从头节点出发，相邻字符不等的最长路径长度
	MaxPath         int // 整棵树上，相邻字符不等的最长路径长度
}
 
var (
	graph [][]int
	S     string
)
 
func longestPath(parent []int, s string) int {
	S = s
	n := len(parent)
	graph = make([][]int, n)
	for i := range graph {
		graph[i] = []int{}
	}
	for i := 1; i < n; i++ {
		graph[parent[i]] = append(graph[parent[i]], i)
	}
	return f(0).MaxPath
}
 
func f(node int) Info {
	if len(graph[node]) == 0 {
		// 叶子节点
		return Info{1, 1}
	}
	max1 := 0 // 从子节点出发的最长链
	max2 := 0 // 从子节点出发的次长链
	maxPath := 1
	for _, child := range graph[node] {
		childInfo := f(child)
		maxPath = max(maxPath, childInfo.MaxPath)
		if S[node] != S[child] {
			// node 和 child 相同的话就不符合相邻字符不等的要求了
			if childInfo.MaxPathFromHead > max1 {
				max2 = max1
				max1 = childInfo.MaxPathFromHead
			} else if childInfo.MaxPathFromHead > max2 {
				max2 = childInfo.MaxPathFromHead
			}
		}
	}
	maxPathFromHead := max1 + 1
	maxPath = max(maxPath, max1+max2+1)
	return Info{maxPathFromHead, maxPath}
}

题目3.移除子树后的二叉树高度

题目描述

给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个独立的查询，其中第 i 个查询你需要执行以下操作：

从树中移除以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不等于根节点的值。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

查询之间是独立的，所以在每个查询执行后，树会回到其初始状态。
树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

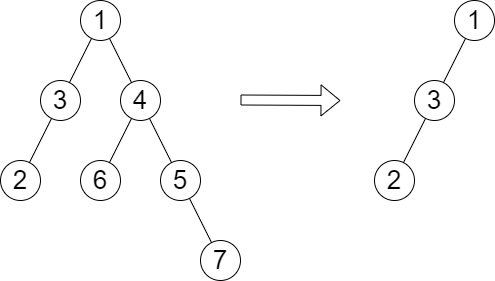
输入：root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]

输出：[2]

解释：上图展示了从树中移除以 4 为根节点的子树。树的高度是 2（路径为 1 -> 3 -> 2）。

示例 2：

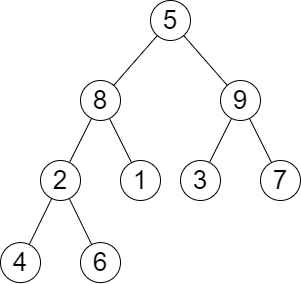
输入：root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]

输出：[3,2,3,2]

解释：执行下述查询：

移除以 3 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 4）。

移除以 2 为根节点的子树。树的高度变为 2（路径为 5 -> 8 -> 1）。

移除以 4 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 6）。

移除以 8 为根节点的子树。树的高度变为 2（路径为 5 -> 9 -> 3）。

提示：

树中节点的数目是 n
2 <= n <= 10^5
1 <= Node.val <= n
树中的所有值 互不相同
m == queries.length
1 <= m <= min(n, 10^4)
1 <= queries[i] <= n
queries[i] != root.val

测试链接

2458.移除子树后的二叉树高度

思路

dfn[i]：节点原始值 i 的 dfn 序
size[i]：dfn 序为 i 的子树节点数
deep[i]：dfn 序为 i 的子树深度

除去节点原始值 i：找到 dfn 序 j = dfn[i]，找到节点个数 s = size[j]，其子树 dfn 为 j~j+s-1，相当于在 deep 中去除 j~j+s-1 位置取最大值就是答案

如何快速计算去除连续一段子数组的数组最大值？

maxL[i]：0~i 中最大值
maxR[i]：i~n-1 中最大值

答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
 
const (
	MAXN = 1e5 + 2
)
 
var (
	dfnCnt = 1
	dfn    = [MAXN]int{}
	size   = [MAXN]int{}
	deep   = [MAXN]int{}
	maxL   = [MAXN]int{}
	maxR   = [MAXN]int{}
)
 
func treeQueries(root *TreeNode, queries []int) []int {
	dfnCnt = 1
	f(root, 0)
	for i := 1; i < dfnCnt; i++ {
		maxL[i] = max(maxL[i-1], deep[i])
	}
	maxR[dfnCnt] = 0
	for i := dfnCnt - 1; i >= 1; i-- {
		maxR[i] = max(maxR[i+1], deep[i])
	}
	m := len(queries)
	ans := make([]int, m)
	for i := 0; i < m; i++ {
		leftMax := maxL[dfn[queries[i]]-1]
		rightMax := maxR[dfn[queries[i]]+size[dfn[queries[i]]]]
		ans[i] = max(leftMax, rightMax)
	}
	return ans
}
 
// 来到 node 节点，从头节点到 node 节点经过了 k 条边
// 填好 dfn、size、deep
func f(node *TreeNode, k int) {
	i := dfnCnt
	dfnCnt++
	dfn[node.Val] = i
	size[i] = 1
	deep[i] = k
	if node.Left != nil {
		f(node.Left, k+1)
		size[i] += size[dfn[node.Left.Val]]
	}
	if node.Right != nil {
		f(node.Right, k+1)
		size[i] += size[dfn[node.Right.Val]]
	}
}

题目4.从树中删除边的最小分数

题目描述

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8，最小异或值是 3，分数是 8 - 3 = 5。

返回在给定树上执行任意删除边方案可能的最小分数。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10^8
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树

测试链接

2322.从树中删除边的最小分数

思路

无向图如何保证递归不会再从子节点递归回父节点？

题目1 方法：递归函数参数传入父节点，判断将要进入下层递归的是不是传入的父节点
本题方法：递归函数参数无需传入父节点，判断将要进入下层递归的节点有没有分配 dfn 序即可

题目没告诉哪个节点是头节点，因为是无向图，所以任取一点为头节点即可

答案

const (
	MAXN = 1001
)
 
var (
	theNums []int
	graph   [][]int
	dfnCnt  = 1
	dfn     = [MAXN]int{}
	size    = [MAXN]int{}
	xor     = [MAXN]int{}
)
 
func minimumScore(nums []int, edges [][]int) int {
	n := len(nums)
	theNums = nums
	graph = make([][]int, n)
	for i := range graph {
		graph[i] = []int{}
	}
	for _, edge := range edges {
		// 无向图
		graph[edge[0]] = append(graph[edge[0]], edge[1])
		graph[edge[1]] = append(graph[edge[1]], edge[0])
	}
	dfnCnt = 1
	for i := 0; i < n; i++ {
		dfn[i] = 0
	}
	f(0)
 
	m := len(edges)
	a, b := 0, 0
	minn, mid := 0, 0
	num1, num2, num3 := 0, 0, 0
	ans := math.MaxInt
	// 遍历两条要删除的边：O(n^2)
	for i := 0; i < m; i++ {
		a = max(dfn[edges[i][0]], dfn[edges[i][1]])
		for j := i + 1; j < m; j++ {
			b = max(dfn[edges[j][0]], dfn[edges[j][1]])
			if a < b {
				minn = b
				mid = a
			} else {
				minn = a
				mid = b
			}
			// minn 是最小的子树
			// mid 是第二小子树
			// 1 是整棵树
			num1 = xor[minn]
			if minn < mid+size[mid] {
				// minn 是 mid 的子树
				num2 = xor[mid] ^ xor[minn]
				num3 = xor[1] ^ xor[mid]
			} else {
				// minn 不是 mid 的子树
				num2 = xor[mid]
				num3 = xor[1] ^ xor[mid] ^ xor[minn]
			}
			ans = min(ans, max(num1, num2, num3)-min(num1, num2, num3))
		}
	}
	return ans
}
 
// 当前来到原始编号 node，遍历 node 的整棵树
// 填好 dfn、size、xor
func f(node int) {
	i := dfnCnt
	dfnCnt++
	dfn[node] = i
	size[i] = 1
	xor[i] = theNums[node]
	for _, child := range graph[node] {
		if dfn[child] != 0 {
			// 防止从子再递归回到父
			// 有 dfn 序就代表遍历过，也就是父节点
			continue
		}
		f(child)
		size[i] += size[dfn[child]]
		xor[i] ^= xor[dfn[child]]
	}
}

备注

掌握 $O (n^{2})$ 的解即可，时间复杂度更好的解分析过程非常繁琐，用到启发式合并

不具备教学意义，有兴趣的同学可以研究

题目5.选课

题目描述

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习

在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习

现在有 N 门功课，每门课有个学分，每门课有一门或没有直接先修课

若课程 a 是课程 b 的先修课即只有学完了课程 a，才能学习课程 b

一个学生要从这些课程里选择 M 门课程学习

问他能获得的最大学分是多少

数据规模：

1 ≤ N ≤ 300
1 ≤ M ≤ 300
1 ≤ ki ≤ N，ki 表示第 i 门课的直接先修课，为 0 代表没有直接先修课
1 ≤ si ≤ 20，si 表示第 i 门课的学分

测试链接

P2014【CTSC1997】选课

普通解法

邻接表建图 + 相对好懂的动态规划

dp[i][j][k]：来到 i 号节点为头的子树，只在 i 号节点、及其 i 号节点下方的前 j 棵子树上挑选节点，一共挑选 k 个节点，并且保证挑选的节点符合先修课设定，最大的累加和

不要最后一个子树（即 j-1 的子树）：dp[i][j-1][k]，只在前 j-1 课子树中选
要最后一个子树（分配给最后一个子树 s 个名额，1 <= s < k）：dp[i][j-1][k-s] + dp[last][len(graph[last])][s]，前 j-1 课子树中选 k-s 个 + 最后一个子树选 s 个

几乎所有题解都是普通解法的思路，只不过优化了常数时间、做了空间压缩

但时间复杂度依然是 $O (n * 每个节点的孩子平均数量 * m^{2})$

其中 $O (n * 每个节点的孩子平均数量 * m)$ 是 dp 表大小， $O (m)$ 是每个格子的枚举代价

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 301
)
 
var (
	n     int
	m     int
	ki    int
	graph = [MAXN][]int{} // 邻接表
	nums  = [MAXN]int{}
	cache = [MAXN][][]int{}
)
 
func init() {
	for i := range graph {
		graph[i] = []int{}
	}
}
 
func main() {
	// s := `7  4
	// 2  2
	// 0  1
	// 0  4
	// 2  1
	// 7  1
	// 7  6
	// 2  2`
	// in := bufio.NewScanner(strings.NewReader(s))
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		// 节点编号 0~n
		n, _ = strconv.Atoi(in.Text())
		in.Scan()
		m, _ = strconv.Atoi(in.Text())
		// 我们将没有直接先修课 0 也看作一个节点，所以要 +1
		m++
		build()
		for i := 1; i <= n; i++ {
			in.Scan()
			ki, _ = strconv.Atoi(in.Text())
			graph[ki] = append(graph[ki], i)
			in.Scan()
			nums[i], _ = strconv.Atoi(in.Text())
		}
		fmt.Fprintln(out, compute())
	}
	out.Flush()
}
 
func build() {
	for i := 0; i <= n; i++ {
		clear(graph[i])
	}
}
 
func compute() int {
	for i := 0; i <= n; i++ {
		cache[i] = make([][]int, len(graph[i])+1)
		for j := range cache[i] {
			cache[i][j] = make([]int, m+1)
			for k := range cache[i][j] {
				cache[i][j][k] = -1
			}
		}
	}
	return f(0, len(graph[0]), m)
}
 
// 当前来到 i 号节点为头的子树
// 只在 i 号节点、及其 i 号节点下方的前 j 棵子树上挑选节点
// 一共挑选 k 个节点，并且保证挑选的节点符合先修课设定
// 返回最大的累加和
func f(i, j, k int) int {
	if k == 0 {
		// 没有节点可挑
		return 0
	}
	if j == 0 || k == 1 {
		// 下面没有子树了，或者只有一个节点名额
		// 那么就只能调当前节点
		return nums[i]
	}
	if cache[i][j][k] != -1 {
		return cache[i][j][k]
	}
	// 不考虑最后一颗子树，在前面的子树中选
	ans := f(i, j-1, k)
	// last：最后一颗子树的头节点
	last := graph[i][j-1]
	for s := 1; s < k; s++ {
		// 在前面的子树中选 k-s 个节点，在最后一颗子树上选 s 个节点
		ans = max(ans, f(i, j-1, k-s)+f(last, len(graph[last]), s))
	}
	cache[i][j][k] = ans
	return ans
}

最优解

链式前向星建图 + dfn 序的利用 + 巧妙定义下的尝试

时间复杂度 $O (n * m)$ ，觉得难可以跳过，这个最优解是非常巧妙和精彩的！

从 dfn 序由大往小推，推到某个节点可以确定是否要，不要的话其子树也不能要

dp[i][j]：i~n+1 dfn 序（原始序号 0~n，dfn 序 1~n+1）中选 j 个节点，保证挑选的节点符合先修课设定，最大的累加和

不选 i 节点：dp[i+size[i]][j]，i 不选的话，要保证挑选的节点符合先修课设定，则 i 的子树也不能选
选 i 节点：dp[i+1][j-1] + vals[i]，选了 i，再从 i+1~n+1 中选，名额少一个

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 301
)
 
var (
	n    int
	m    int
	ki   int
	nums = [MAXN]int{}
	dp   = [MAXN + 2][MAXN]int{} // +2: dfn 序多一个，i+size[i] 也可能多一个
 
	// 链式前向星
	edgeCnt = 1
	head    = [MAXN]int{}
	next    = [MAXN]int{}
	to      = [MAXN]int{}
 
	// dfn
	dfnCnt = 1
	size   = [MAXN + 1]int{} // +1: 原始序号 0~n，dfn 序 1~n+1
	vals   = [MAXN + 1]int{} // dfn 序的 nums
)
 
func main() {
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		// 节点编号 0~n
		n, _ = strconv.Atoi(in.Text())
		in.Scan()
		m, _ = strconv.Atoi(in.Text())
		build()
		for i := 1; i <= n; i++ {
			in.Scan()
			ki, _ = strconv.Atoi(in.Text())
			addEdge(ki, i)
			in.Scan()
			nums[i], _ = strconv.Atoi(in.Text())
		}
		fmt.Fprintln(out, compute())
	}
	out.Flush()
}
 
func build() {
	edgeCnt = 1
	dfnCnt = 1
	for i := 0; i <= n; i++ {
		head[i] = 0
	}
	for i := 0; i <= m; i++ {
		dp[n+2][i] = 0
	}
}
 
func addEdge(f, t int) {
	next[edgeCnt] = head[f]
	to[edgeCnt] = t
	head[f] = edgeCnt
	edgeCnt++
}
 
func compute() int {
	f(0)
	// 节点编号 0 ~ n，dfn 序范围 1 ~ n+1
	// 接下来的逻辑其实就是 01 背包！不过经历了很多转化
	// 整体的顺序是根据 dfn 序来进行的，从大的 dfn 序，遍历到小的 dfn 序
	// dp[i][j]: i ~ n+1 范围的节点，选择 j 个节点，保证挑选的节点符合先修课设定，最大的累加和
	// 怎么定义符合先修课设定？重点！重点！重点！
	// 假设 i ~ n+1 范围上，目前所有头节点的上方，有一个总的头节点
	// i ~ n+1 范围所有节点，选出来 j 个节点的结构，
	// 挂在这个假想的总头节点之下，是一个连续的结构，没有断开的情况
	// 那么就说，i ~ n+1 范围所有节点，选出来 j 个节点的结构是符合先修课设定
	for i := n + 1; i >= 2; i-- {
		for j := 1; j <= m; j++ {
			dp[i][j] = max(dp[i+size[i]][j], dp[i+1][j-1]+vals[i])
		}
	}
	// dp[2][m]: 2 ~ n+1 范围上，选择 m 个节点，保证挑选的节点符合先修课设定，最大的累加和
	// 最后来到 dfn 序为 1 的节点，一定是原始的 0 号节点
	// 原始 0 号节点下方一定挂着有符合先修课设定
	// 并且和补充的 0 号节点一定能整体连在一起，没有任何跳跃连接
	// 于是整个问题解决
	return vals[1] + dp[2][m]
}
 
// 填好 size、vals
// 返回 node 这颗子树的 size
func f(node int) int {
	i := dfnCnt
	dfnCnt++
	size[i] = 1
	vals[i] = nums[node]
	for ei := head[node]; ei > 0; ei = next[ei] {
		size[i] += f(to[ei])
	}
	return size[i]
}

备注

最优解属于动态规划的状态设计优化，还属于启发式合并

这两个部分的内容会在【扩展】、【挺难】课程里安排

My-Notes

全部文章

061.树型dp-下

dfn 序

备注

题目1.到达首都的最少油耗

题目描述

测试链接

思路

答案

题目2.相邻字符不同的最长路径

题目描述

测试链接

答案

题目3.移除子树后的二叉树高度

题目描述

测试链接

思路

答案

题目4.从树中删除边的最小分数

题目描述

测试链接

思路

答案

备注

题目5.选课

题目描述

测试链接

普通解法

最优解

备注

目录

关系图谱