032.双指针技巧与相关题目

前置知识：无

设置两个指针的技巧，其实这种说法很宽泛，似乎没什么可总结的

1. 有时候所谓的双指针技巧，就单纯是代码过程用双指针的形式表达出来而已，没有单调性（贪心）方面的考虑（题目1、题目2）
2. 有时候的双指针技巧包含单调性（贪心）方面的考虑，牵扯到可能性的取舍。对分析能力的要求会变高。其实是先有的思考和优化，然后代码变成了双指针的形式（题目 3～7）

所以，双指针这个“皮”不重要，分析题目单调性（贪心）方面的特征，这个能力才重要

常见的双指针类型：

• 同向双指针
• 快慢双指针
• 从两头往中间的双指针
• 其他

题目1.按奇偶排序数组 II

题目描述

给定一个非负整数数组 nums，  nums 中一半整数是 奇数 ，一半整数是 偶数 。

对数组进行排序，以便当 nums[i] 为奇数时，i 也是 奇数 ；当 nums[i] 为偶数时， i 也是 偶数 。

你可以返回任何满足上述条件的数组作为答案。

测试链接

922.按奇偶排序数组 II

思路

一个指针指向奇数位、一个指针指向偶数位，看最后一个数是奇是偶，“发货”到指针指向的奇偶位置。直到奇偶指针其一越界，说明奇数或偶数都已到达正确位置，那么另一种数也一定都到了正确位置

答案

func sortArrayByParityII(nums []int) []int {
	n := len(nums)
	for even, odd := 0, 1; even < n && odd < n; {
		if nums[n-1]&1 == 1 {
			nums[odd], nums[n-1] = nums[n-1], nums[odd]
			odd += 2
		} else {
			nums[even], nums[n-1] = nums[n-1], nums[even]
			even += 2
		}
	}
	return nums
}

备注

不同的说法，同一个题：给定一个数组 arr，请把 arr 调整成奇数都在奇数位置或者偶数都在偶数位置

题目2.寻找重复数

题目描述

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

提示：

• 1 <= n <= 10^5
• nums.length == n + 1
• 1 <= nums[i] <= n
• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

测试链接

287.寻找重复数

答案

寻找重复数

题目3.接雨水

测试链接

42.接雨水

思路

每个位置能接多少雨水：max(0, min(左侧最大值, 右侧最大值) - 当前值)

从左往右遍历一遍，求出各位位置的前缀最大值辅助数组；从右往左遍历一遍，求出各位位置的后缀最大值辅助数组

遍历数组，利用两个辅助数组可以求每个位置能接多少雨水

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

思考和优化后：左右双指针

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

答案

接雨水

备注

二维接雨水问题，会在宽度优先遍历的章节讲述，后续的【必备】课程

题目4.救生艇

题目描述

给定数组 people 。people[i] 表示第 i 个人的体重 ，船的数量不限，每艘船可以承载的最大重量为 limit。

每艘船最多可同时载两人，但条件是这些人的重量之和最多为 limit。

返回承载所有人所需的最小船数。

测试链接

881.救生艇

思路

数组先排序，贪心的思路，代码的过程用双指针的形式表达出来

答案

func numRescueBoats(people []int, limit int) int {
	sort.Ints(people)
	n := len(people)
	l, r := 0, n-1
	ans := 0
	for l <= r {
		weight := people[l] + people[r]
		if l == r {
			weight = people[l]
		}
		ans++
		if weight <= limit {
			l++
			r--
		} else {
			r--
		}
	}
	return ans
}

复杂度

• 时间复杂度：$O(n\ast lon{g}^n)$，排序的复杂度
• 空间复杂度：$O(1)$

拓展

以上条件都不变，再增加一个要求：如果两人一船那么体重之和必须是偶数，又该怎么做？（大厂真考过）

答：将数组分成奇偶两个数组，各自进行如上思路，将答案加起来即可

因为奇数加奇数是偶数、偶数加偶数是偶数，而奇数加偶数必然是奇数，所有分开讨论，各自算自己的

题目5.盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：

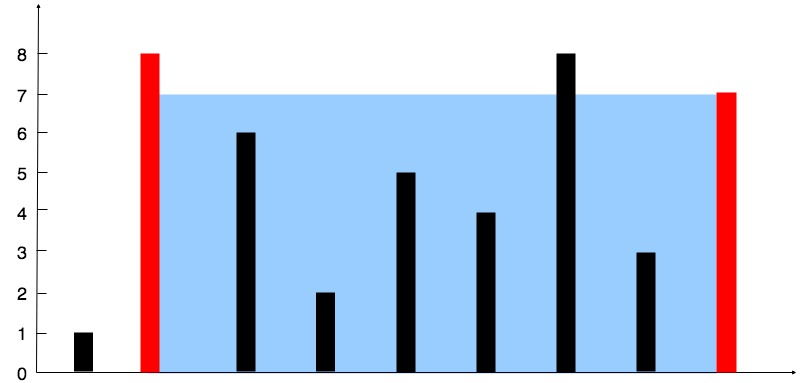
输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49

测试链接

11.盛最多水的容器

思路

左右双指针，谁小结算谁

小的那个是瓶颈，将来不会出现以小的那个为一边的更优解，因为两个指针不断向中间移动，距离越来越近，只可能比当前盛水更少

答案

func maxArea(height []int) int {
	n := len(height)
	l, r := 0, n-1
	ans := 0
	for l < r { // l, r 必须是两个柱子，所以不能相等
		if height[l] < height[r] {
			ans = max(ans, height[l]*(r-l))
			l++
		} else {
			ans = max(ans, height[r]*(r-l))
			r--
		}
	}
	return ans
}

复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

题目6.供暖器

题目描述

冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。

在加热器的加热半径范围内的每个房屋都可以获得供暖。

现在，给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置，请你找出并返回可以覆盖所有房屋的最小加热半径。

注意：所有供暖器 heaters 都遵循你的半径标准，加热的半径也一样。

测试链接

475.供暖器

思路

找出每个房屋选取的最优供暖器

答案

var (
	theHouses  []int
	theHeaters []int
	n          int
	m          int
)
 
func findRadius(houses []int, heaters []int) int {
	sort.Ints(houses)
	sort.Ints(heaters)
	n = len(houses)
	m = len(heaters)
	theHouses = houses
	theHeaters = heaters
	// i 号房子
	i := 0
	// j 号供暖器
	j := 0
	ans := 0
	for i < n && j < m {
		for !best(i, j) {
			j++
		}
		ans = max(ans, abs(houses[i]-heaters[j]))
        i++
	}
	return ans
}
 
// 当前的地点 houses[i] 由 heaters[j] 来供暖是最优的吗？
// 当前的地点 houses[i] 由 heaters[j] 来供暖，产生的半径是 a
// 当前的地点 houses[i] 由 heaters[j+1] 来供暖，产生的半径是 b
// 如果 a < b, 说明是最优，供暖不应该跳下一个位置
// 如果 a >= b, 说明不是最优，应该跳下一个位置
// 注意：= 一定要跳下一个位置，如果有多个供暖器都在这个位置，那么会一直不跳，卡在这里
func best(i, j int) bool {
	return j+1 == m || abs(theHouses[i]-theHeaters[j]) < abs(theHouses[i]-theHeaters[j+1])
}
 
func abs(n int) int {
	if n < 0 {
		return -n
	}
	return n
}

复杂度

• 时间复杂度：$O(n\ast lon{g}^n)$，排序的复杂度
• 空间复杂度：$O(1)$

题目7.缺失的第一个正数

题目描述

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

测试链接

41.缺失的第一个正数

思路

移动数组元素位置，将数组变成 [1, 2, 3, ...]，从哪一位开始无法变成，那一位就是没有出现的最小的正整数

答案

func firstMissingPositive(nums []int) int {
	n := len(nums)
	// l: l 左侧已归位
	// 归位: [1, 2, 3, ...]，即：nums[i] == i + 1
	// 永远盯着 l 位置的数字看，看能不能扩充(l++)
	l := 0
	// r: r-1 右侧为垃圾区；
	// 最好的状况下，认为 1~r 是可以收集全的，每个数字收集 1 个，不能有垃圾
	// 有垃圾呢？预期就会变差(r--)
	r := n
	// [l, r)
	for l < r {
		if nums[l] == l+1 { // 已归位
			l++
		} else if nums[l] < l+1 || nums[l] > r || nums[l] == nums[nums[l]-1] {
			// 垃圾
			// nums[l] < l+1: nums[l] 不是正数，或 nums[l] 处已经归位了，又来一个就是垃圾
			// nums[l] > r: 比我需要的位置还大
			// nums[l] == nums[nums[l]-1]: 右边的那个位置已经归位了
			r--
			swap(nums, l, r)
		} else {
			// 对其归位
			swap(nums, l, nums[l]-1)
		}
	}
	return l + 1
}
 
func swap(arr []int, i, j int) {
	arr[i], arr[j] = arr[j], arr[i]
}

缺失的第一个正数

复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$