004.梯度下降

有一个成本函数 $J(w_1,w_2,...,w_n,b)$，目标是计算 $\underset{w_1,w_2,...,w_n,b}{\mathrm{minimize}}J(w_1,w_2,...,w_n,b)$

梯度下降是一种可用于尝试最小化这个成本函数的算法

1. 对参数 $w_1,w_2,...,w_n,b$ 做初始估计：在线性回归中初始值是什么不重要，所以常见的做法是把它们都设为 0
2. 不断改变参数，使得成本函数减小
3. 直到成本函数到达最小值或接近最小值：一个成本函数可能不止一个最小值

梯度下降步骤

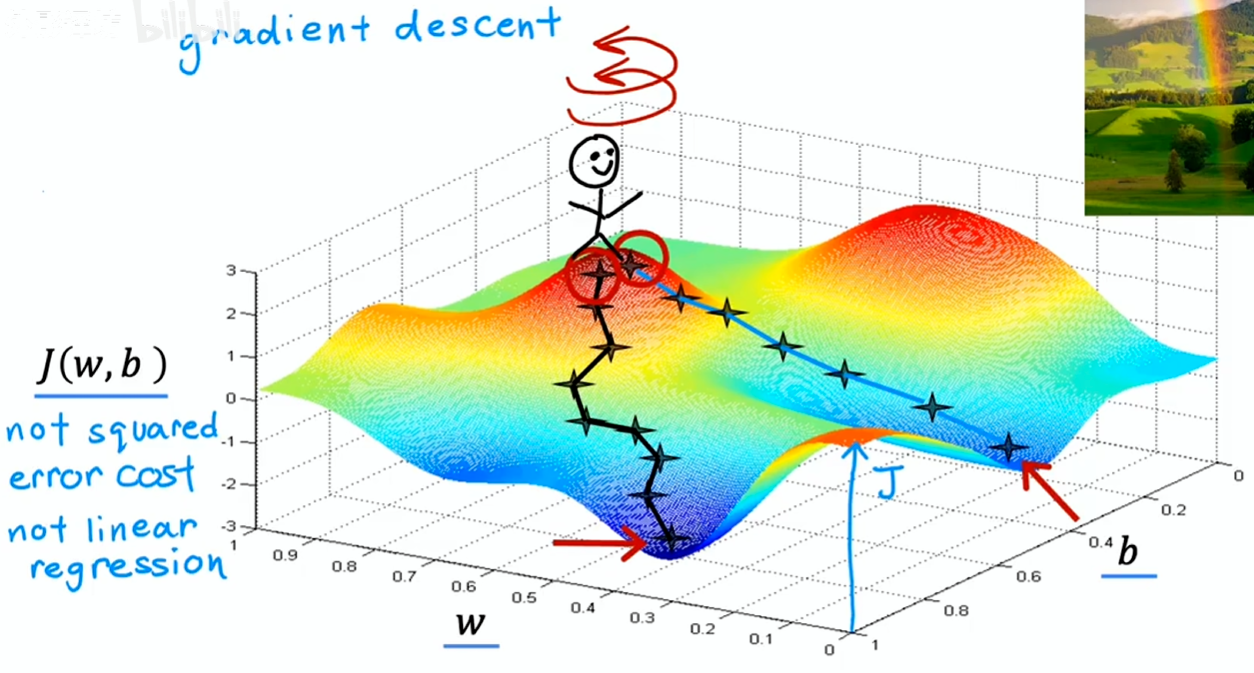
多步梯度下降：

1. 目标是从初始参数出发，尽快到达其中一个山谷底部
2. 梯度下降算法会让你转一圈，并自问“该朝哪个方向迈一小步，能够快速下山”——即数学上的最陡下降方向
3. 然后迈出一小步到达一个新位置，然后重复该步骤——找最陡下降方向继续迈步
4. 直到到达这个山谷底部的局部最小值处

选择不同的初始参数，经过多步梯度下降到达的局部最小值可能不同

梯度下降公式

$$重复直到收敛\{\begin{array}{c}w=w-\alpha \frac{\partial }{\partial w}J(w,b)\\ b=b-\alpha \frac{\partial }{\partial b}J(w,b)\end{array}$$

根据当前 w、b 的值调整更新 w、b

• $\alpha$：学习率，是一个介于 0~1 之间的小正数，作用是控制向下走的步长大小
• $\frac{\partial }{\partial w}J(w,b)$：成本函数的导数项，作用是控制该朝哪个方向迈步

重复以上更新步骤，直到算法收敛，即到达了局部最小值点，在该点参数 w 和 b 随着每一步的增加变化不再显著

细节：要同时更新两个参数 w、b

右侧非同时更新的结果或多或少还是能行得通，但并未是实现梯度下降算法的正确方式

导数项作用

为了简便，设 b = 0

$\frac{\partial }{\partial w}J(w)$ 表示横轴为 $w$，纵轴为 $J(w)$ 的斜率

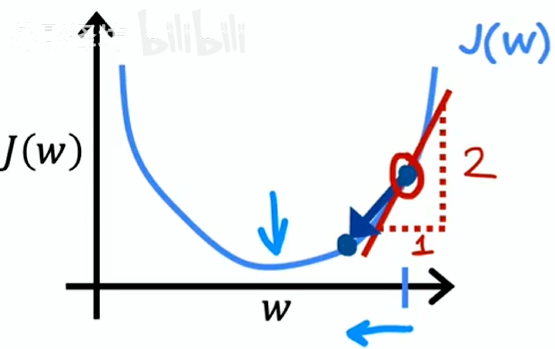
这种情况斜率为正数，$w=w-\alpha 正数$，w 会变小，更接近最小值

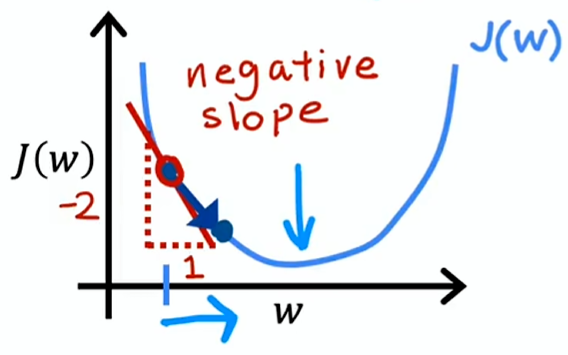
这种情况斜率为负数，$w=w-\alpha 负数$，w 会变大，也是更接近最小值

学习率

学习率 $\alpha$，是一个介于 0~1 之间的小正数，作用是控制向下走的步长大小

学习率太小

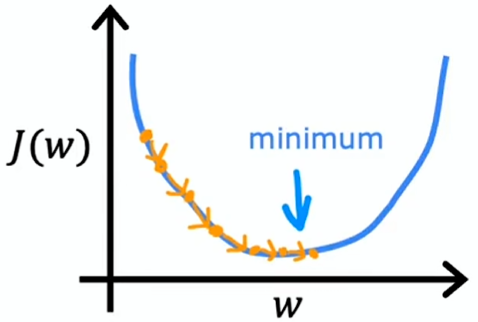
若学习率太小，梯度下降算法能起到作用，但速度会很慢（每一步只走很小距离，需要很多步才能到达局部最小），会花费很长时间

学习率太大

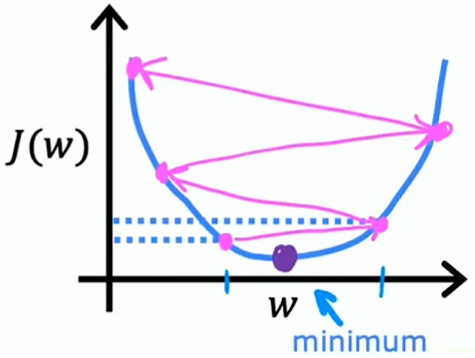
若学习率太大，梯度下降算法可能会过头，可能永远到不了局部最小，即梯度下降无法收敛，甚至可能发散

达到局部最小

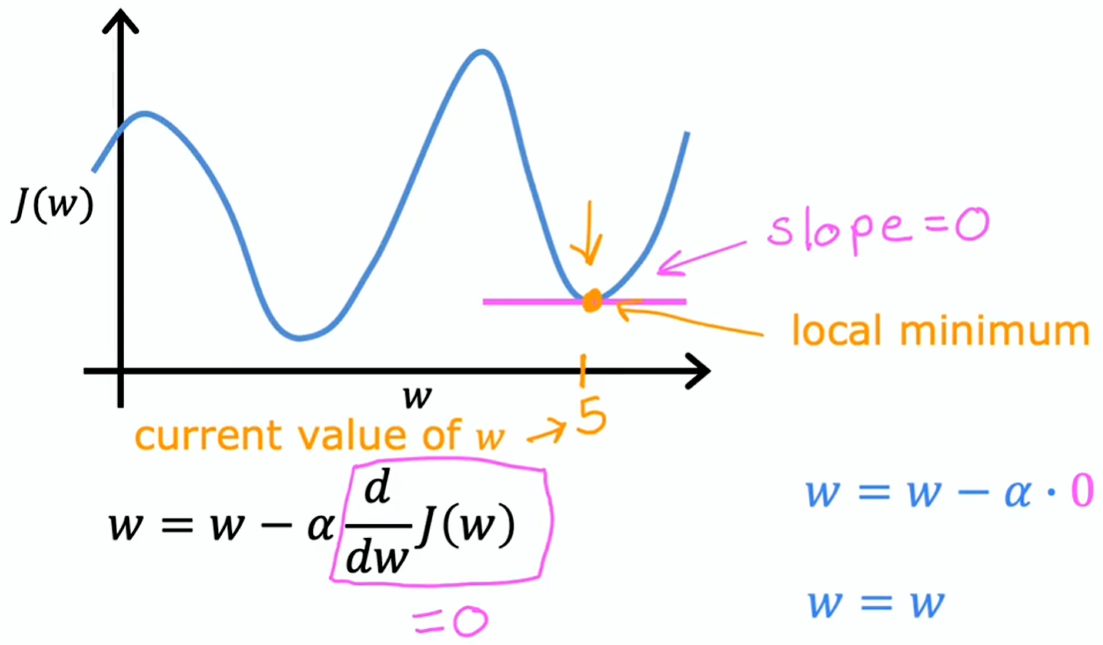
已到达局部最小，则参数不会更新了。能够让解维持在那个局部最小值

这也解释了为何即便学习率固定，梯度下降仍能达到局部最小值

斜率越大，导数项越大，即便学习率固定，步长也越大。接近局部最小时，梯度下降会自动减小步长，这是由于当靠近局部最小值时斜率变小，步长也会变小（即便学习率固定）

用于线性回归的梯度下降

• 线性回归模型：$f_{w,b}(x)=wx+b$
• 成本函数：$J(w,b)=\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$
• 梯度下降公式：

$$重复直到收敛\{\begin{array}{l}w=w-\alpha \frac{\partial }{\partial w}J(w,b)=w-\alpha \frac{1}{m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}\\ b=b-\alpha \frac{\partial }{\partial b}J(w,b)=b-\alpha \frac{1}{m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})\end{array}$$

计算过程：

$$\{\begin{array}{l}\frac{\partial }{\partial w}J(w,b)=\frac{\partial }{\partial w}\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})2x^{(i)}=\frac{1}{m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}\\ \frac{\partial }{\partial b}J(w,b)=\frac{\partial }{\partial b}\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2=\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})2=\frac{1}{m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})\end{array}$$

线性回归使用平方误差成本函数时，成本函数不会有多个局部最小值，因其呈弓形所以有唯一的全局最小值。对此的专业术语是此代价函数为凸函数

凸函数：呈弓形的函数，除唯一全局最小值外不会有其他局部最小值

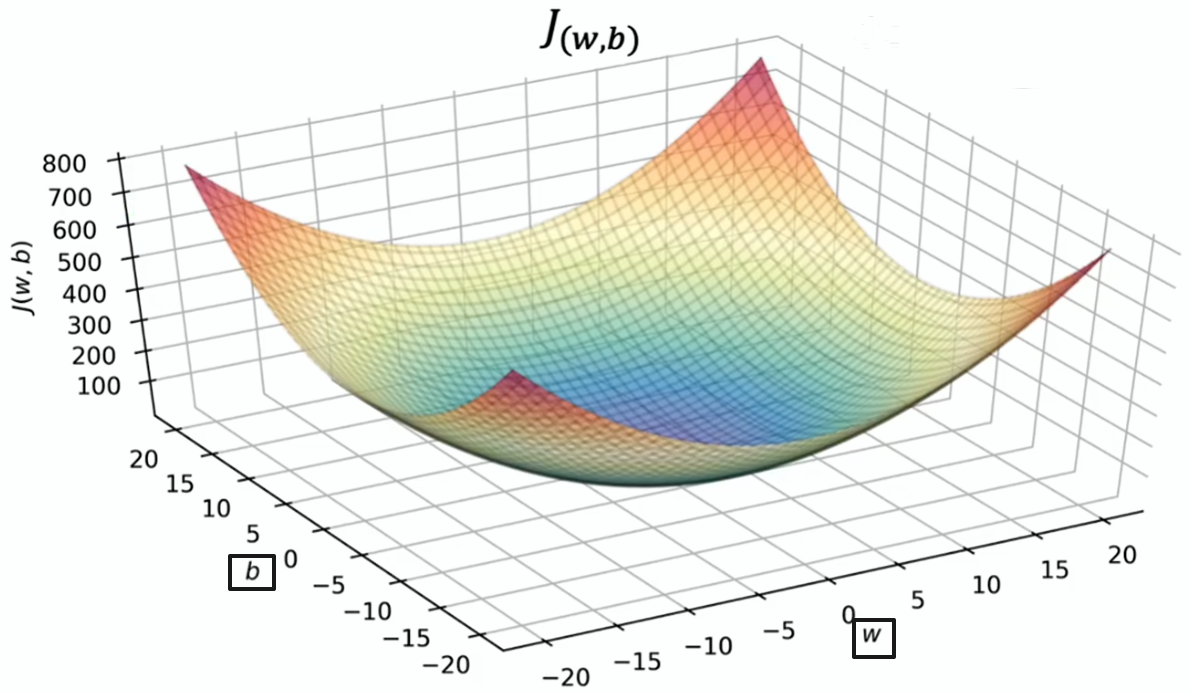
当对凸函数执行梯度下降时，只要学习率选择恰当，它总能收敛到全局最小值

批量梯度下降

批量梯度下降：在梯度下降的每一步，看的是所有训练样本而不只是训练数据的一部分

还有其他版本的梯度下降，它们不会考虑整个训练集，而是在每次更新步骤查看训练数据的较小子集

我们将在线性回归中使用批量梯度下降