多维特征
之前都是只考虑一个特征 x,下面了解多维特征
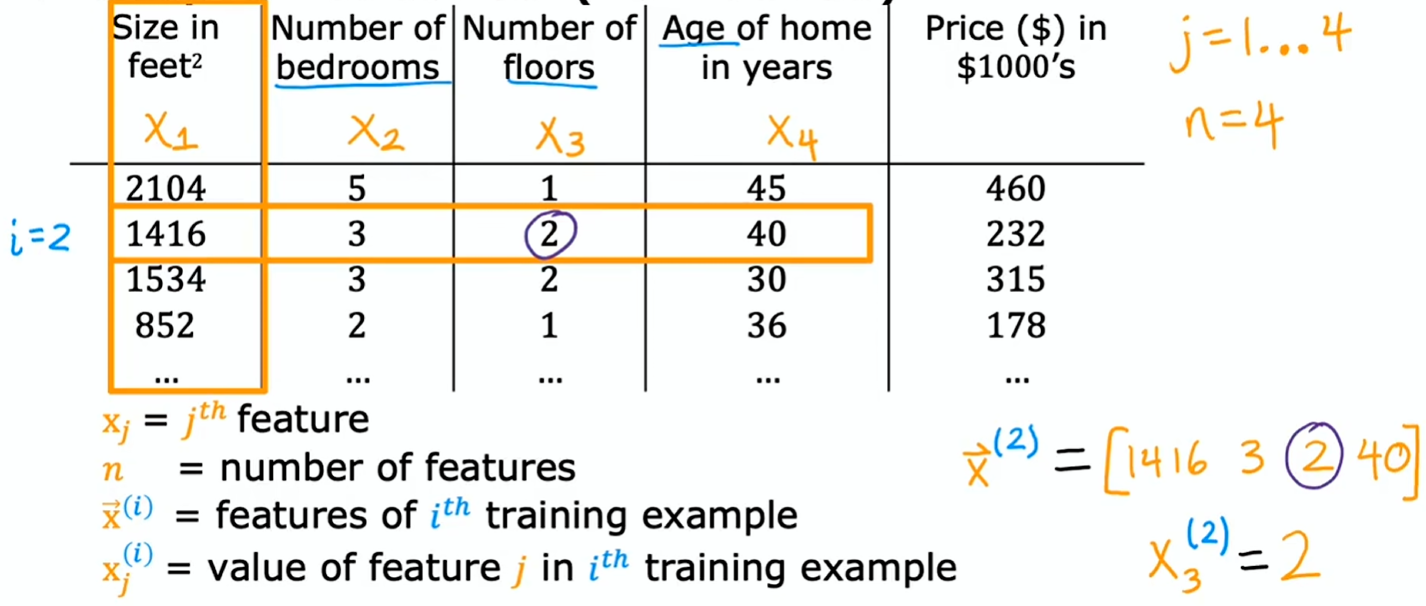
- :第 个特征,如:
- :特征的数量
- :第 个训练样本,是一个由 个数字组成的列表,可以称为向量。它包含了第 个训练示例的所有特征
- 可以将箭头视为一个可选的指示符,仅用于强调 表示向量,而非一个数字
- :指代第 个训练样本中的第 个特征
模型表示
- 之前:
- 现在:
为了书写简化:
- 表示参数向量(箭头可省略)
- 是一个数字
- 表示特征向量(箭头可省略)
所以上面式子中的 和 都是向量,即:
其中 可以写为点积形式
最终写为
这种带有多个输入特征的线性回归模型,称为多元线性回归 (multiple linear regression)
向量化
当你在实现一个学习算法时,使用向量化会让你的代码更简洁,并且能让它运行得更高效
学习如何编写向量化代码能让你利用现代数值线性代数库,甚至可能还能利用 GPU 硬件
举个例子:3 维特征
- 是一个数字
# np 来于 NumPy 库,是 python 和机器学习领域目前应用最广泛的数值线性代数库
w = np.array([1.0, 2.5, -3.3])
b = 4
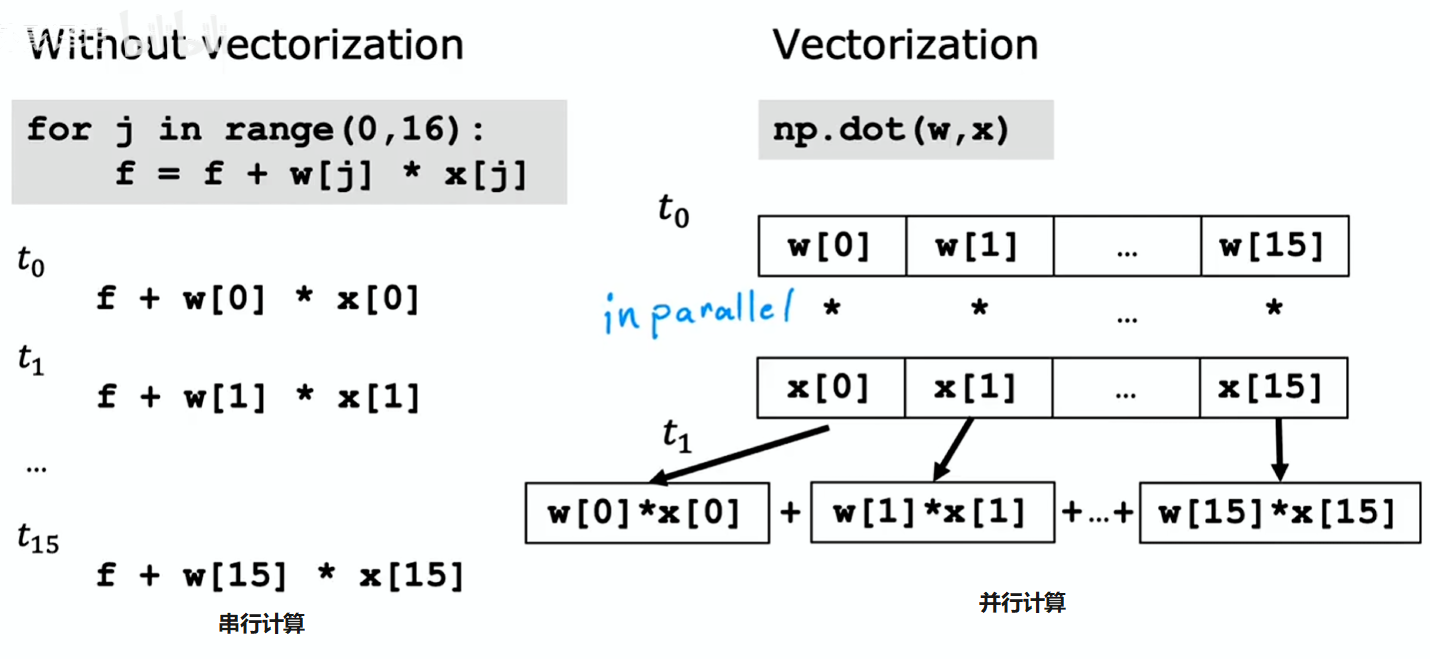
x = np.array([10, 20, 30])计算模型预测时不进行向量化的实现方法 1:
f = w[0] * x[0] +
w[1] * x[1] +
w[2] * x[2] + b计算模型预测时不进行向量化的实现方法 2:
f = 0
for j in range(0, n): # range(0, n) 表示 j = 0, 1, ..., n-1
f = f + w[j] * x[j]
f = f + b使用向量化 (Vectorization):
f = np.dot(w, x) + b- 代码简洁
- 运行速度快:
np.dot函数能够利用计算机中的并行硬件(如 GPU 或 CPU)
梯度下降计算
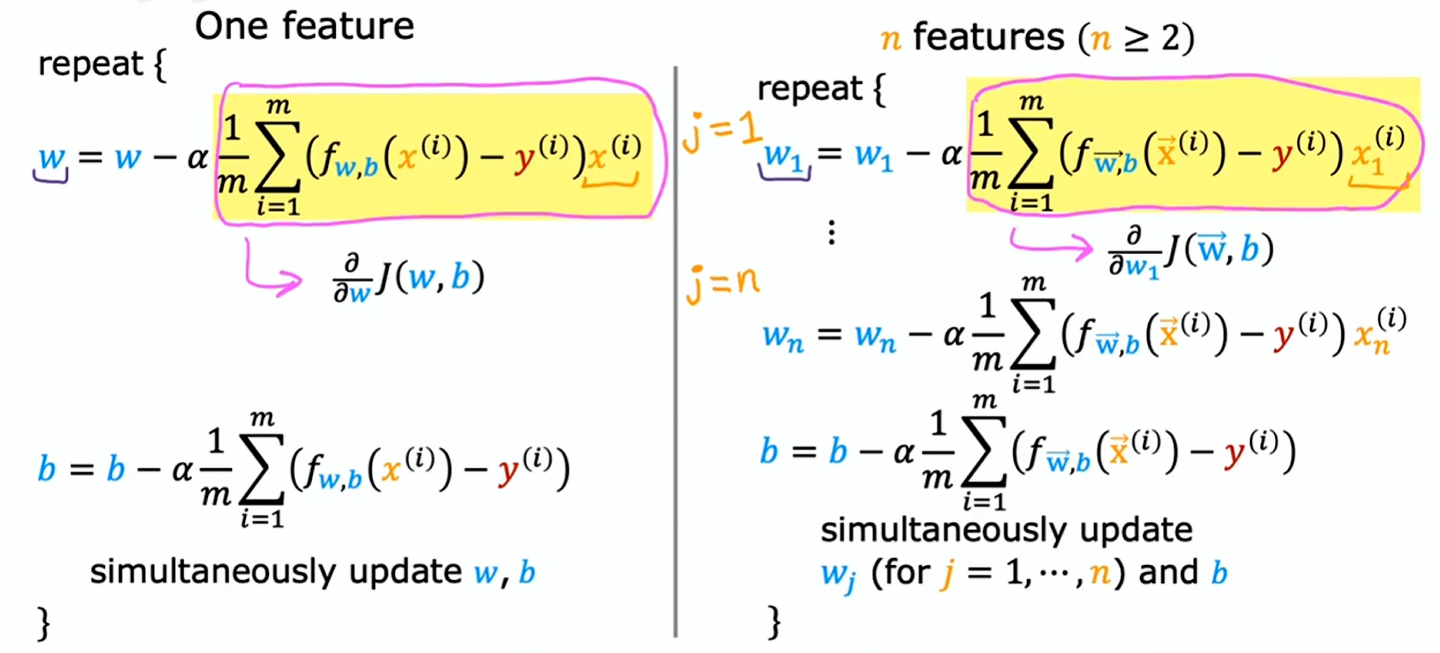
令
- 参数:
- 导数项:
w = np.array([0.5, 1.3, ..., 3.4])
w = np.array([0.3, 0.2, ..., 0.4])不使用向量化计算梯度下降:
for j in range(0, 16):
w[j] = w[j] - 0.1 * d[j]使用向量化计算梯度下降:
w = w - 0.1 * d通过向量化实现多元线性回归的梯度下降
| 之前的表示法 | 向量表示法 | |
|---|---|---|
| 参数 | | |
| 模型 | ||
| 成本函数 | ||
| 梯度下降 |
梯度下降的替代方案
正态方程 (Normal equation) 仅适用于线性回归,不需要迭代就能找出参数
正态方程的缺点:
- 仅适用于线性回归,无法推广到其他学习算法
- 当特征数量较多时(> 10,000)变慢
无需太过关心正态方程如何运作的细节,只需留意一些机器学习库可能在后台使用此复杂方法求解
但对于大多数学习算法(包括你自己),如何实现线性回归,梯度下降通常是完成这项工作的更好方法