模型评估

如何评估一个模型的性能？

诊断就是运行的一个测试，以深入了解学习算法的好坏，并获得提高其性能的指导

具体做法是将训练样本按 7:3 或 8:2 分割为训练集和测试集，测试集数据仅用于测试模型性能，而不参与训练

算法在未训练过的示例上的性能，能更好地表明模型在新数据上的表现

模型选择

如果要拟合一个预测房价或其他回归问题的函数，你可能会考虑的模型是一阶到 d 阶多项式，并得出它们在测试集上的表现来选择模型，但这不是最佳方法

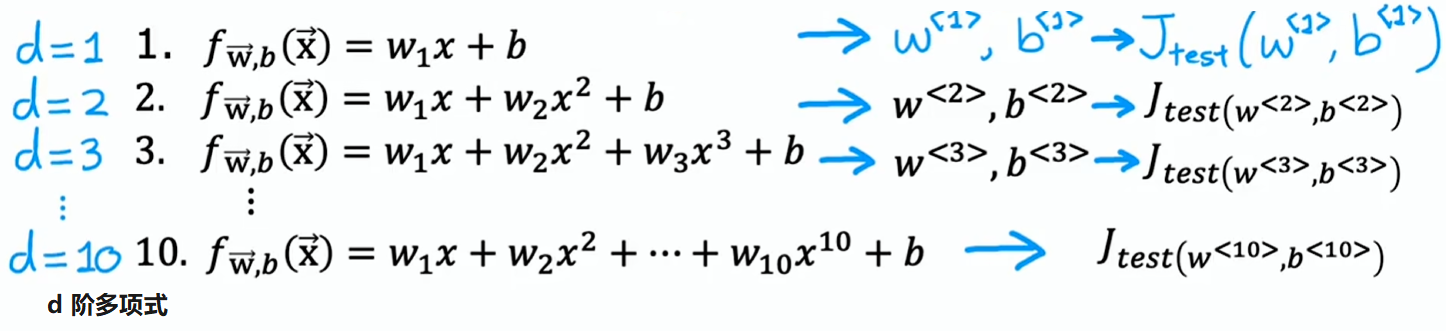
此方法存在缺陷的原因是：假设五阶多项式表现最佳， $J_{t es t} (w^{< 5 >}, b^{< 5 >})$ 很可能是对泛化误差做出了乐观估计。换句话说，它很可能低于实际的泛化误差，原因在于上图讨论的基本拟合过程中有一个额外的参数 $d$ （多项式的次数），而我们使用测试集选择了这个参数（ $d = 5$ ）

修正办法：不是把数据只分成两个子集（训练集和测试集），而是把数据分成三个不同子集（称为训练集、交叉验证集、测试集）

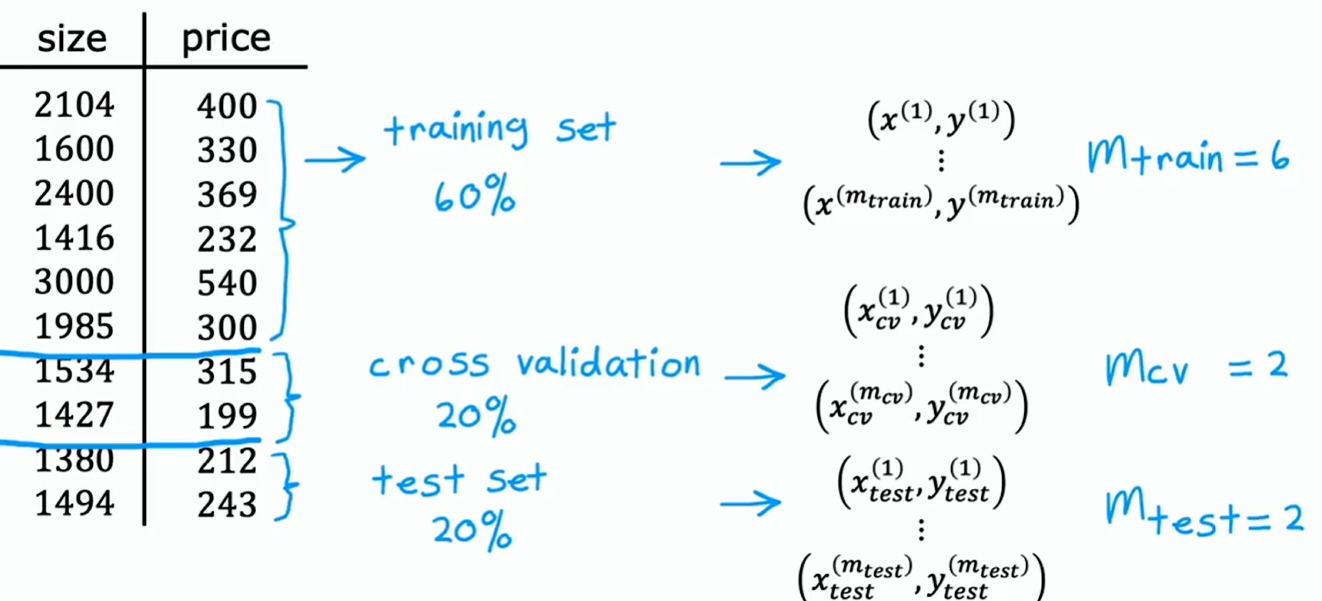
要用交叉验证集来检查或交叉检验不同模型的有效性或确切地说是准确性

简称它为验证集（validation set）或开发集（development set）

有了三个数据集，可以计算训练误差、交叉验证误差和测试误差，这些项均不包含训练目标中的正则化项

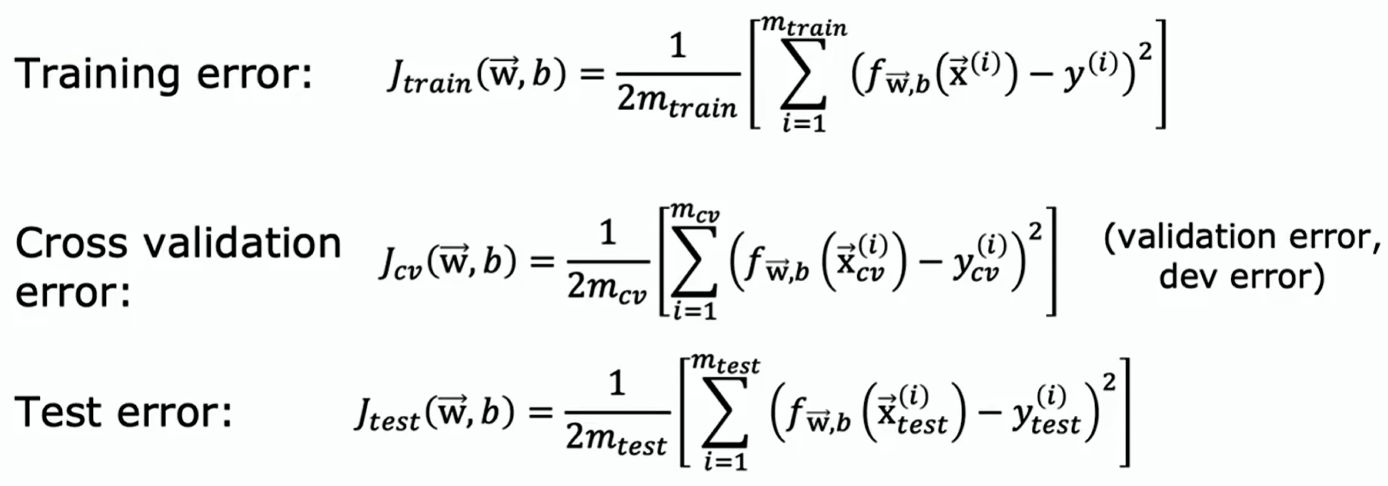
可以像前面那样使用一阶到 d 阶多项式模型，然后拟合参数 $W$ 和 $b$ ，但不要在测试集上对其进行评估，而是要在交叉验证集上评估这些参数，并计算 $W$ 、 $b$ 的 $J_{c v}$ ；然后为选择一个模型，查看哪个模型的交叉验证误差最低，假如四阶多项式表现最佳，即 $J_{c v} (w^{< 4 >}, b^{< 4 >})$ 最小；最后，如果想报告一个关于这个模型在新数据上表现如何的泛化误差估计，将使用测试集来完成此操作，并报告出 $J_{t es t} (w^{< 4 >}, b^{< 4 >})$

在机器学习中这被认为是最佳实践：如果你需要对模型做出决策，例如拟合参数或选择模型架构（如神经网络架构或线性回归中的多项式次数），则应仅使用训练集和交叉验证集来做出所有这些决策，且完全不看测试集。只有在确定了一个模型作为最终模型之后才能在测试集上评估它，而且你没有依据测试集做任何决策，这能确保你的测试集是公平的，不会对模型在新数据上的泛化效果做出过于乐观的估计

通过偏差与方差进行诊断

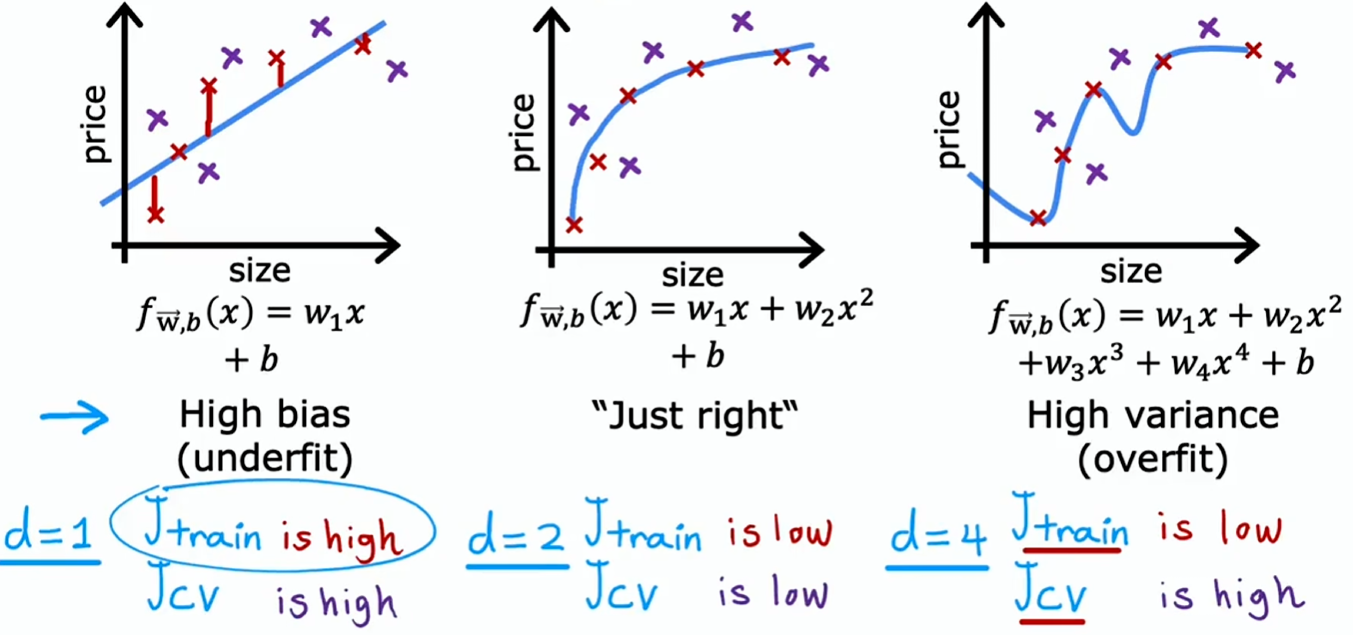
之前绘制了单特征高偏差（high bias）或高方差（high variance）的直观表现图标。但如果有更多特征，就难以绘制图表，也难以轻易直观判断其表现

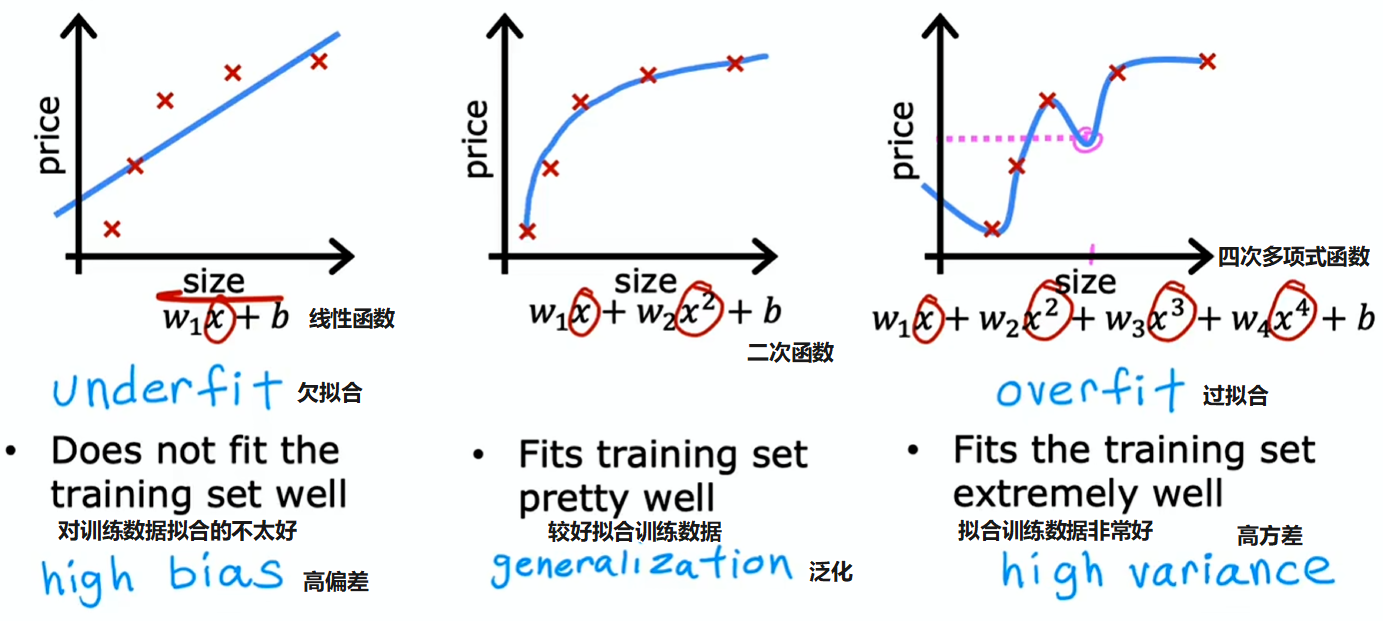
与其试图查看这样的图表，一种更系统的诊断方式或找出算法是否存在高偏差或高方差的方法，就是要看算法在训练集和交叉验证集上的表现：

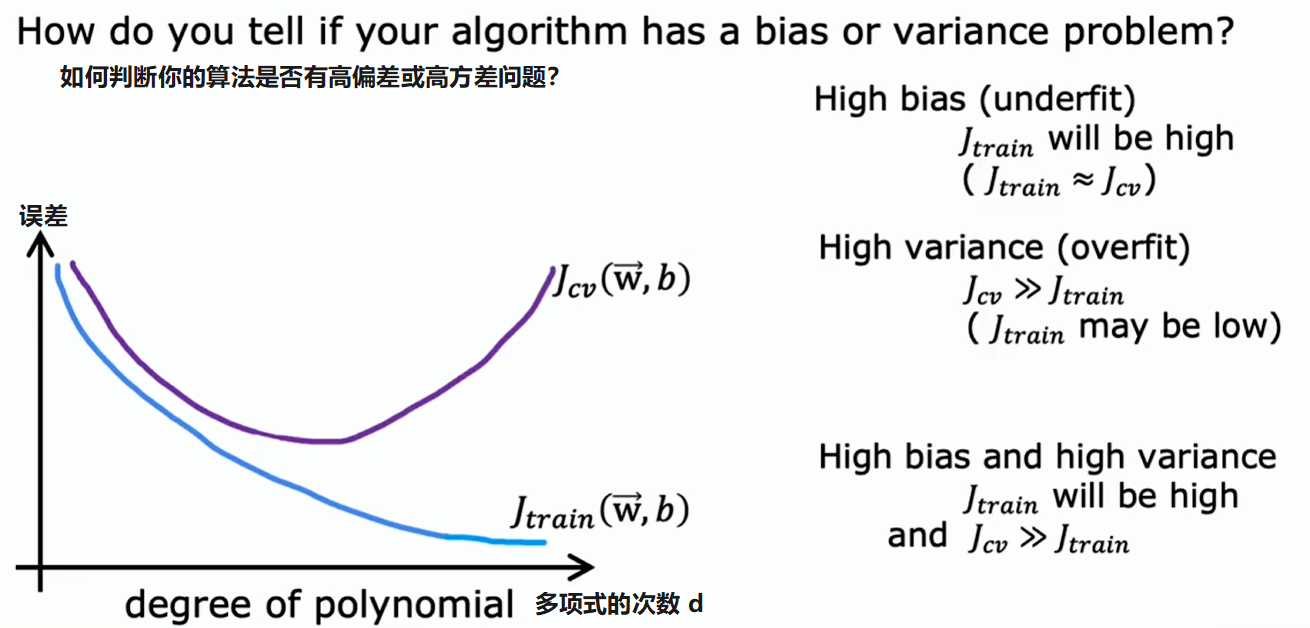
正则化参数 $λ$ 的选择如何影响偏差和方差：

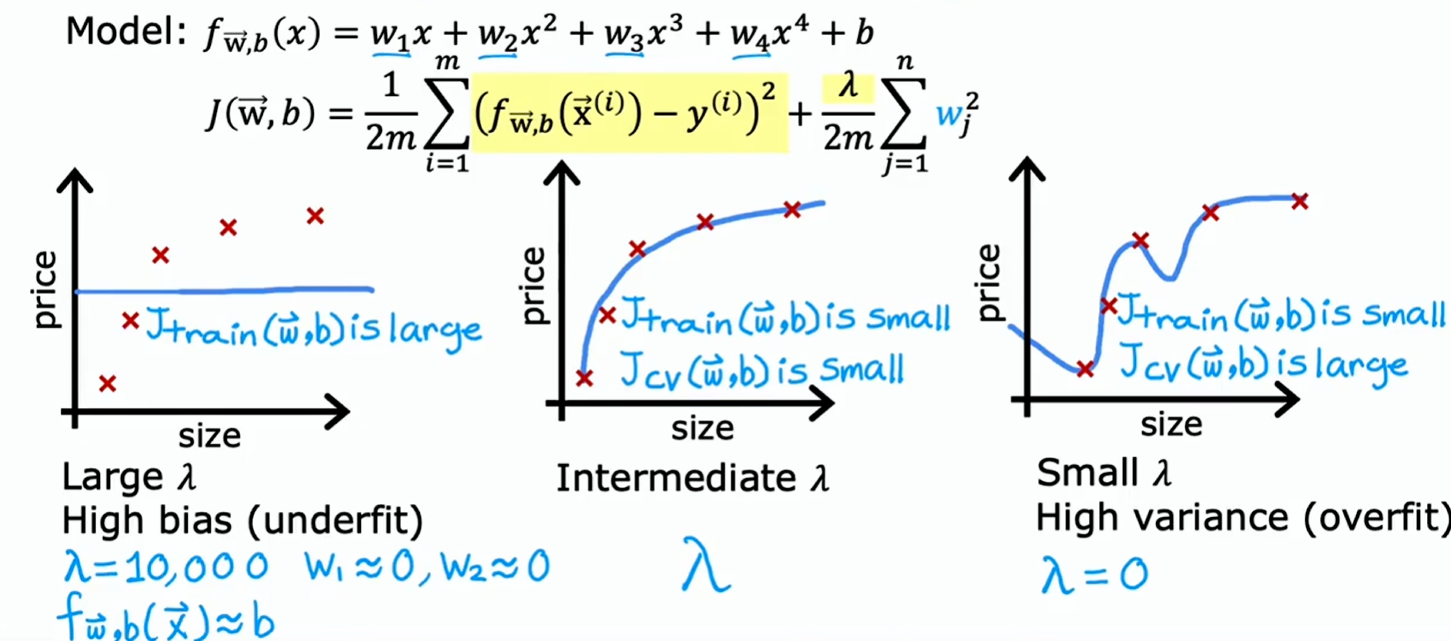
$λ$ 取极大数，则正则化项极大，会迫使模型选择 $w$ 参数极其接近 0，即： $f \approx b$ ，欠拟合
$λ$ 取 0 或接近 0，则正则化项为 0 或接近 0，即：忽略正则化

如果你正在尝试决定正则化参数 $λ$ 的最佳值，交叉验证也为你提供了一种方法来实现这一点。这类似于之前看到的用于通过交叉验证选择多项式阶数 $d$ 的过程：

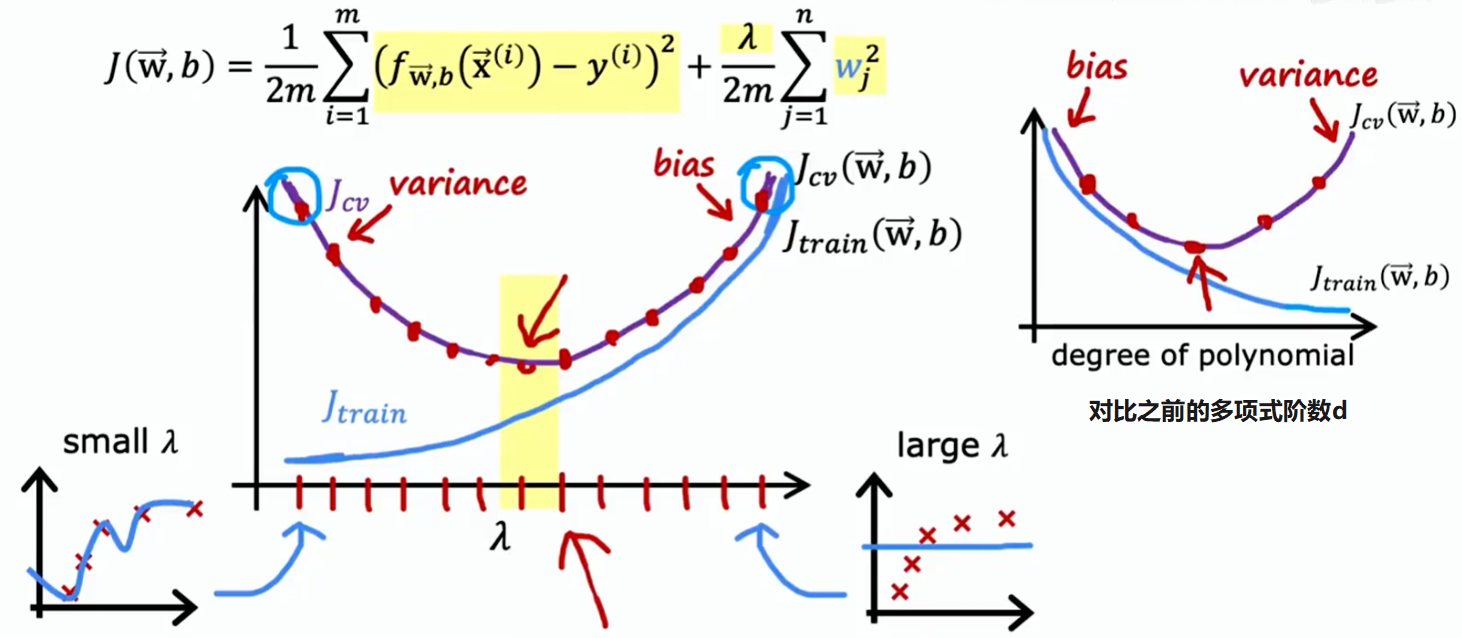
衡量偏差与方差

例如一个模型语音转文字的模型：

在训练集的错误率是 10.8%
在验证集的错误率是 14.8%

如何衡量它的偏差与方差呢？看起来 10.8% 错误率偏差挺大的

但事实证明，还有一件事也很值得考量，也就是人类的表现水平如何？

人类在训练集的错误率是 10.6%

因为语音中存在噪音，即使是人类也无法听清说的什么

所以判断模型是否存在高偏差与高方差，要有一个衡量参考

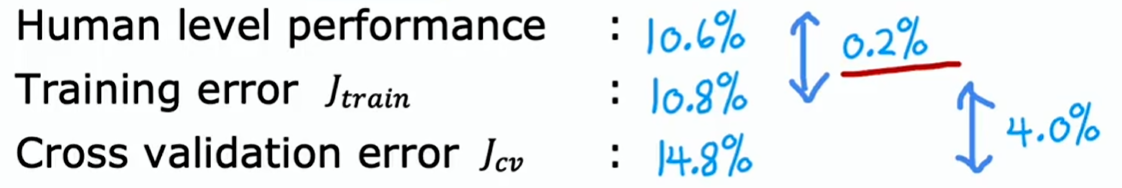
结论是：这个算法的方差问题比偏差问题更突出

所以在判断训练误差是否偏高时，建立性能基线往往很有用，性能基线是指你合理期望学习算法最终能达到的误差水平是多少？

建立性能基线水平的常用方法，比如：

衡量人类在这项任务上能做到多好
是否有某种竞争算法，可能是其他人实现的先前版本，甚至是竞争对手的算法
根据先前的经验进行猜测

那么在判断一个算法是否具有高偏差或高方差时，要查看基线性能水平、训练误差、交叉验证误差。要测量的两个关键量是：

训练误差与你希望达到的基线水平之间的差异，代表是否存在高偏差
训练误差与交叉验证误差之间的差距，代表是否存在高方差

学习曲线

学习曲线是一种帮助理解学习算法表现如何随经验量变化的方法。这里的经验指的是，比如它拥有的训练样本数量

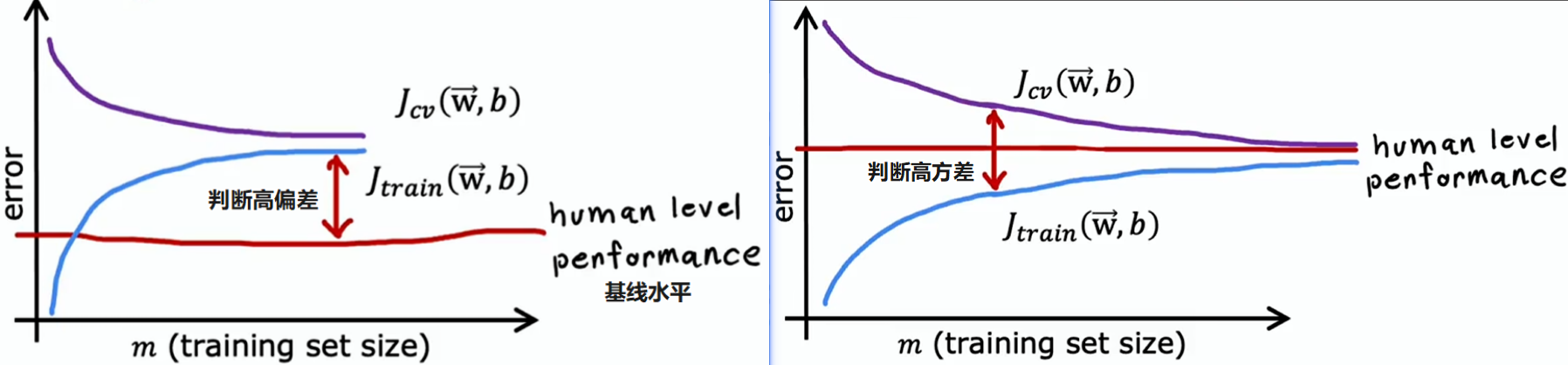
横轴：训练集的规模，即算法可用于学习的示例数量
纵轴：模型在训练集和验证集的误差
训练集误差：随着训练集规模变大，训练集误差会增大（训练集越大，模型越难拟合）
- 高偏差：训练误差曲线可能会开始变平，这是因为随着得到越来越多的训练示例，简单模型不会有太多改变
- 高方差：甚至比基线水平表现还好，或略差于基线水平
验证集误差：交叉验证误差通常会比训练误差高；随着训练集规模变大，模型越来越好，所以交叉验证误差在下降
- 高偏差：同样地交叉验动证集误差下降一段时间后趋于平稳，因为简单模型改变不大
- 高方差：验证集误差远大于训练集误差。增加训练集大小，有望使验证集误差逼近训练集误差

如果你愿意取训练集的不同子集去绘制学习曲线，那么这能让你从另一种方式来查看算法是否存在高偏差还是高方差

但是像这样绘制学习曲线的缺点是计算成本颇高，需要用训练集的不同规模子集去训练这么多不同的模型。所以实际上很少这么做，但即便如此，脑海中浮现不同规模训练集学习曲线的样子，能帮助理清学习算法的运行情况

下一步做什么

通过训练集误差和验证集误差判断算法是高偏差或高方差，能够更好地指导接下来该尝试什么，从而提高学习算法的性能

如果你已经实现了正则化线性回归来预测房价，但你的算法在预测中出现了不可接受的大误差，接下来你会尝试什么？

j (w, b) = \frac{1}{2 m} i = 1 \sum m (f_{w, b} (x^{(i)}) - y^{(i)})^{2} + \frac{λ}{2 m} j = 1 \sum n w_{j}^{2}

解决高偏差：

增大模型灵活性（或说是让模型更强大）
- 尝试使用更多的特征，例如：仅依据房屋面积来预测房价，但事实表明房价还取决于卧室数量、楼层、房龄等特征。除非添加那些额外特征，否则算法永远无法良好拟合
- 添加多项式特征，如： $x_{1}^{2}, x_{2}^{2}, x_{1} x_{2}$ 等
- 减小正则化的影响，即减小 $λ$

解决高方差：

获取更多训练集
减小模型灵活性（或说是简化模型）
- 尝试使用更少的特征
- 增大正则化的影响，即增大 $λ$

注意：不要通过减小训练集规模来解决高偏差问题，这往往会增大交叉验证误差，降低学习算法的性能

大数据

在神经网络时代之前，机器学习工程师们常常需要在偏差和方差之间权衡（模型不要太简单，也不要太复杂），必须平衡多项式次数所代表的复杂度，或者正则化参数 $λ$ ，让偏差和方差都不会过高

但神经网络取得巨大成功的原因之一，是由于神经网络再加上大数据（拥有大量数据集）的理念，为我们提供了一种全新的方式来解决高偏差和高方差问题

事实证明，大型神经网络在小到中等规模数据集上训练时是低偏差模型。也就是说如果将神经网络设置得足够大，几乎总能很好地适配训练集

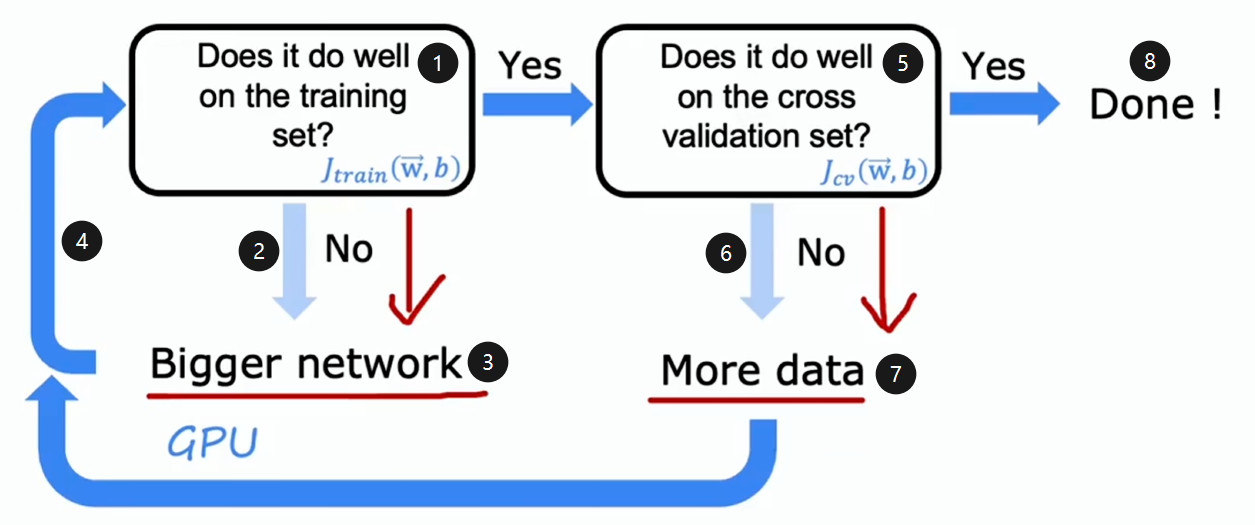
在训练集上训练模型，看它在训练集上表现如何？
如果表现不好，则说明存在高偏差
则使用更大的神经网络
然后重新训练，重复此过程，直到训练良好，即不存在高偏差
之后在验证集进行验证
如果表现不好，则说明存在高方差
就获取更多的训练集，然后回去重新训练模型
不断循环此过程直到它在交叉验证集上表现良好，就大功告成了

当然此方法的应用存在局限性，训练更大的神经网络，其计算成本会变得很高，这就是为什么神经网络的兴起得益于硬件（尤其是 GPU）的发展

但是即便有硬件加速，超过某个点，神经网络变得如此庞大，训练时间如此之长，变得不可行

当然，另一个限制是数据方面的问题，有时所能获取的数据就这么多，超过一定限度后就很难获取更多数据了

如果你有一个小神经网络，然后换成一个大得多的神经网络，你可能会觉得过拟合风险大幅上升，但事实证明若对这个更大的神经网络进行适当正则化，那么这个更大的神经网络通常至少表现一样好，甚至比小的更好

换言之，只要正则化得当，使用更大的神经网络几乎从不有害，但需要注意的是当你训练更大的神经网络时，其计算成本会增加，所以它的主要弊端是会减慢训练和推理过程

TensorFlow 实现正则化：

My-Notes

全部文章

007.偏差和方差