倾斜数据集的误差指标
正例与负例比例严重失衡,那么像准确率这样的常用误差指标效果不佳
假设你在训练一个二元分类器,通过实验室测试来检测患者是否患罕见病
假设你发现在测试集上的误差率为 1%,这看上去是个很不错的结果?
但结果是这是一种罕见疾病,在所有患者中只有 0.5% 患有这种疾病,如果你编写一个程序只输出“y=0”(不患病),它的误差率都只有 0.5%,这个看似简单的算法你的学习算法表现更好,所以无法判断 1% 的误差究竟是好是坏
处理不均衡数据集问题时,通常会使用不同的误差指标。特别要提的是一对常用的误差度量指标是精准率和召回率
在这个例子中,y=1 是罕见类别,用一个罕见类别来评估学习算法的性能,构建一个混淆矩阵会很有用,它是一个 的矩阵
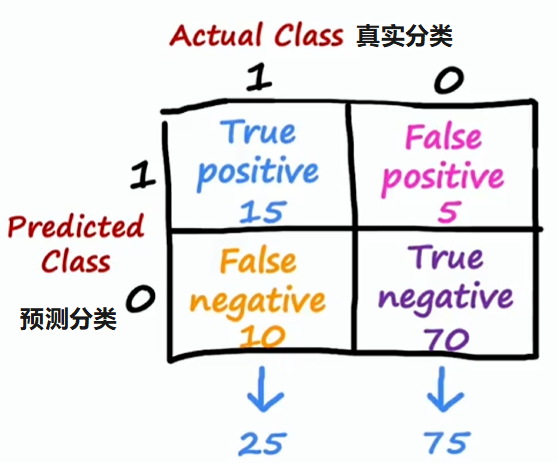
- 真阳性(true positive):实际为 1 且预测为 1
- 真阴性(true negative):实际为 0 且预测为 0
- 假阳性(false positive):实际为 0 但预测为 1
- 假阴性(false negative):实际为 1 但预测为 0
精准率和召回率
- 精准率(Precision):
- 在所有预测为阳性的样本中,实际做对的比例
- 本例中:若算法诊断出一名患者患罕见病,那患者真有此病的比例
- 真阳数量/所有预测为阳数量,
- 在本例中为
- 召回率(Recall):
- 在所有真实为阳性的样本中,正确检测的比例
- 本例中:若有一名患罕见病的患者,算法正确识别出的比例
- 真阳数量/所有实际为阳数量,
- 在本例中为
在理想情况下,我们希望学习算法具有高精度和高召回率;但实际上,精准度和召回率之间往往需要权衡
一个逻辑回归问题(二分类问题)::
- 如果 则预测为 1
- 如果 则预测为 0
其中 threshold 就是阈值,介于 0~1 之间,一般取 0.5
- 提高阈值,会提高准确率,但降低召回率
- 只有在十分有把握时才会预测患病(y=1)
- 比如当预测患者患有某种疾病时,需要让他们接受可能具有侵入性和昂贵的检查,但疾病的后果没那么糟糕
- 在这种情况下,可以选择设定一个更高的阀值,如 0.7,即:70% 的把握才判定患病
- 降低阈值,会提高召回率,但降低准确率
- 为了安全起见,存疑时要避免遗漏过多罕见疾病的病例
- 比如治疗的侵入性不强或不会带来太大痛苦、花费也不高,但不治疗疾病对患者的后果会严重得多
- 在这种情况下,可以选择设定一个更低的阀值,如 0.3,即:30% 患病几率就要检查
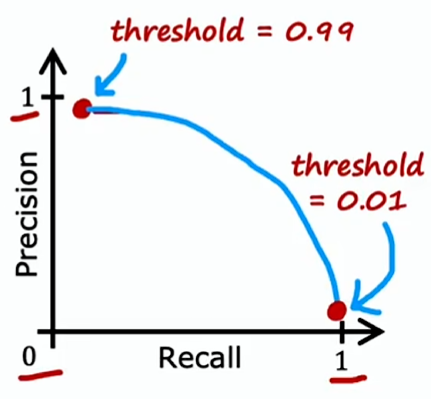
请注意,通过交叉验证并不能真正确定阈值,在许多情况下,需要手动选择阀值来权衡精准率和召回率
如果想自动权衡精准率和召回率,还有一个名为 F1 分数的指标,有时用于自动综合两者的最佳权衡
| Precision (P) | Recall (R) | 平均分 | F1 分 | |
|---|---|---|---|---|
| 算法 1 | 0.5 | 0.4 | 0.45 | 0.444 |
| 算法 2 | 0.7 | 0.1 | 0.4 | 0.175 |
| 算法 3 | 0.02 | 1.0 | 0.501 | 0.0392 |
比如有如上 3 种算法,很难看出该选哪种算法,要是有个算法精准率和召回率都更高,那就选它了。但在本例中,算法 2 的精准率最高,而算法 3 的召回率最高,算法 1 则介于两者之间,因此没有一个算法明显是最佳选择
为了帮助决定选哪种算法,找到一种合并精准率和召回率的方法可能会有用
一种合并的方式是取两者平均值:,但结果证明这不是个好办法,算法 3 的平均分最高,但是它的精准率很低,可能就是之前举例的只输出“y=1”(将所有患者诊断为患病)的程序
F1 分数用于综合衡量精准率与召回率,但它更侧重于两者中的较小值,毕竟结果表明若一个算法的精准率或召回率极低,那它可能没多大用
在数学里,这个公式也叫做 P 和 R 的调和平均数(Harmonic mean),调和平均数是一种求平均值的方式,它更注重较小的值