008.逻辑回归

之前都是介绍线性回归，本节将介绍分类：其中输出变量 $y$ 只能取少数几个可能值之一，而非无限范围内的任意数值

二元分类

二元分类：要预测的变量只能在两个可能值中选其一（是或否）

正类（positive class）	负类（negative class）
yes	no
true	false
1	0

需要明确的是正类/负类不一定意味着好/坏或善/恶的对比，而是传达存在/缺失或是/否的状态

如：

• 检测垃圾邮件：正类表示是垃圾邮件；负类表示不是垃圾邮件
• 检测交易欺诈：正类表示存在欺诈情况；负类表示没有欺诈情况
• 检测恶性肿瘤：正类表示存在恶性肿瘤；负类表示良性肿瘤

其实正类表示是垃圾邮件或正类表示不是垃圾邮件都行的通，不同的工程师可能会把它换过来

线性回归并非解决分类问题的理想算法

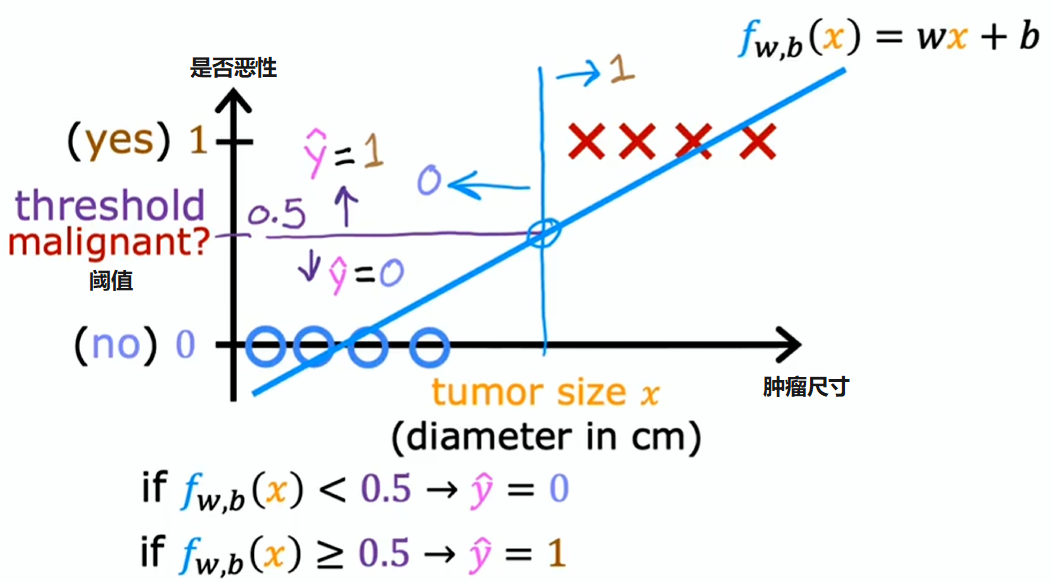
训练集多一个训练样本：

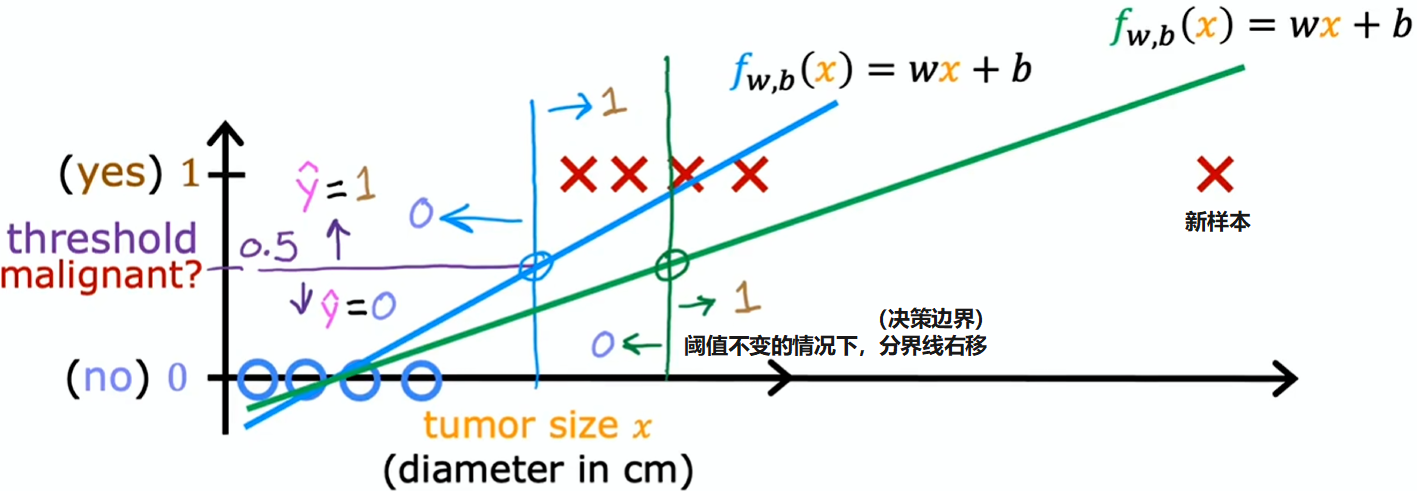
这并非我们所愿，因为在右侧添加的新样本，不应改变对恶性肿瘤与良性肿瘤分类的任何结论

逻辑回归

逻辑回归（logistic regression）这个名字让人困惑，虽然它包含“回归”一词，但实际用来解决二元分类问题（出于历史原因得名）

S 形函数（sigmoid function）也叫逻辑函数（logistic function）

$$g(z)=\frac{1}{1+e^{-z}},0<g(z)<1$$

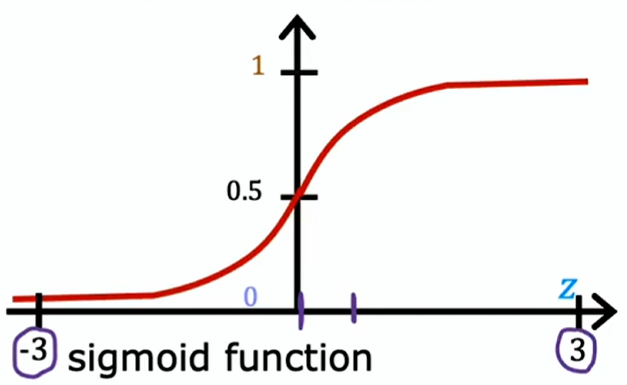
其中 $e$ 为数学常数，值约为 2.7

结合上式得出逻辑回归模型：

$$f_{\vec{w},b}(\vec{x})=g(\vec{w}\cdot \vec{x}+b)=\frac{1}{1+e^z}$$ $$f_{\vec{w},b}(\vec{x})=g(\vec{w}\cdot \vec{x}+b)=\frac{1}{1+e^{-(\vec{w}\cdot \vec{x}+b)}}$$

假设一个结果 $f_{\vec{w},b}(\vec{x})$ 为 0.7，表示的是结果为 1 的可能性是 70%，结果为 0 的可能性是 30%。即：在已知 $x$ 的情况下 $y$ 等于 1 的概率（参数为 $\vec{x},b$）

$$上式f_{\vec{w},b}(\vec{x})=P(y=1|x;\vec{x},b)$$

决策边界

由上式可知 $f_{\vec{w},b}(\vec{x})$ 是一个 0~1 之间的小数（如 0.7 表示结果为 1 的可能性是 70%），但结果只能是 1 或 0，所以需要一个阈值，通常是 0.5

若 $f_{\vec{w},b}(\vec{x})\ge 0.5$，则结果 $\hat{y}=1$；若 $f_{\vec{w},b}(\vec{x})<0.5$，则结果 $\hat{y}=0$

由上图 S 形函数可知 $z\ge 0$（其中 $z=\vec{w}\cdot \vec{x}+b$），则 $\hat{y}=1$；反之 $z<0$，则 $\hat{y}=0$

例 1：有两个特征 $x_1,x_2$，$z=0$ 时的线为决策边界

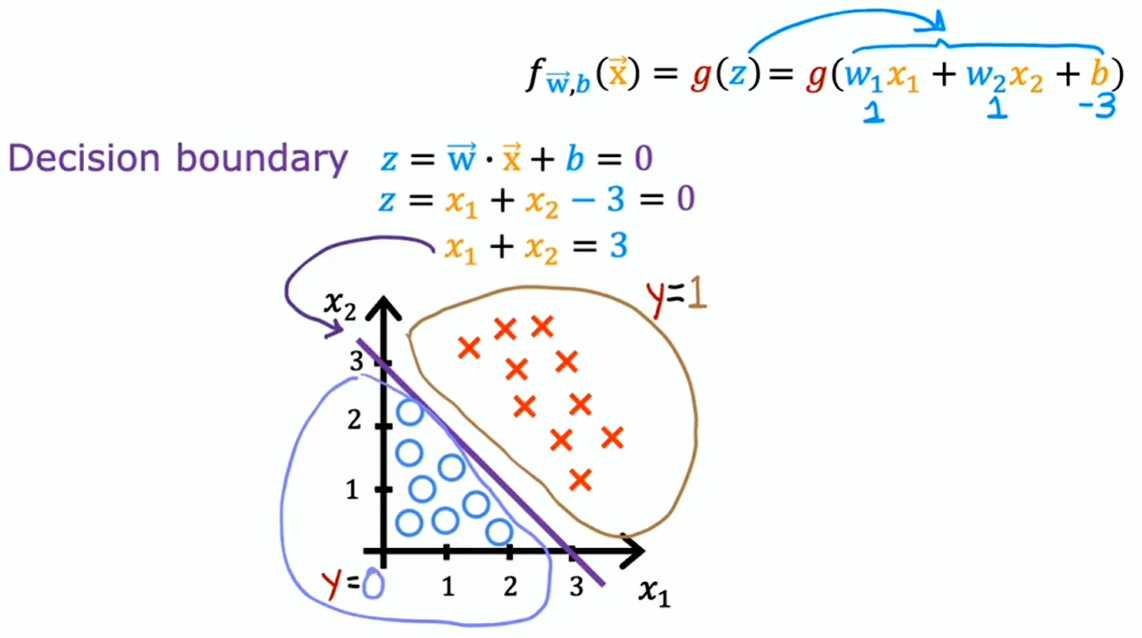
例 2：非线性决策边界

例 2：更高阶多项式的非线性决策边界

成本函数

平方误差成本函数：$J(\vec{w},b)=\frac{1}{m}{\sum }_{i=1}^m\frac{1}{2}(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2$

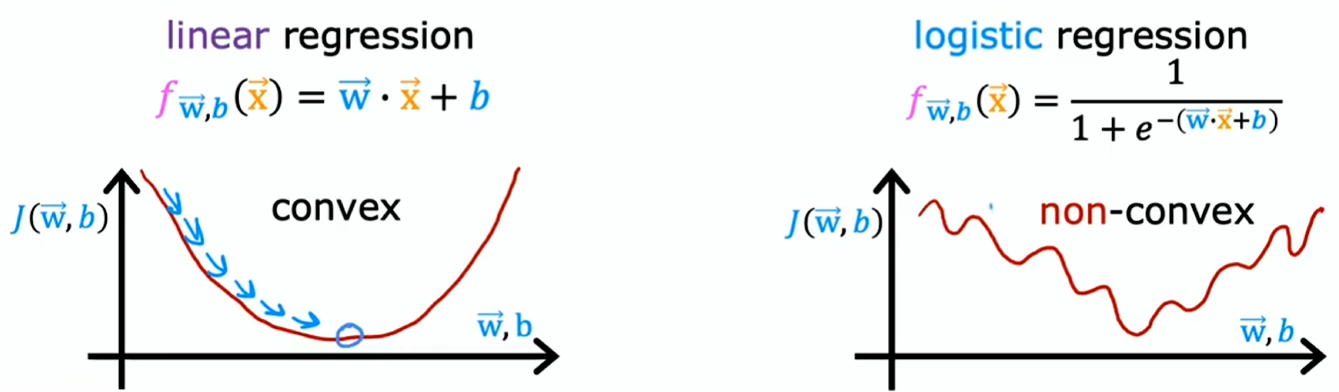
在线性回归中是凸函数，但在逻辑回归中不是凸函数

这意味着想用梯度下降法，会有很多局部最小值让你陷进去，所以对于逻辑回归来说，平方误差成本函数不是个好选择

回到成本函数：$J(\vec{w},b)=\frac{1}{m}{\sum }_{i=1}^m\frac{1}{2}(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2$，其中 $L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=\frac{1}{2}(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2$ 称为单个训练示例上的损失 (Loss)

损失函数衡量的是单个样本上的表现情况，通过对所有训练样本的损失进行求和进而得到成本函数

逻辑损失函数

$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=\{\begin{array}{rc}-log(f_{\vec{w},b}({\vec{x}}^{(i)}))& if{y}^{(i)}=1\\ -log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))& if{y}^{(i)}=0\end{array}$$

$if{y}^{(i)}=1$：

$if{y}^{(i)}=0$：

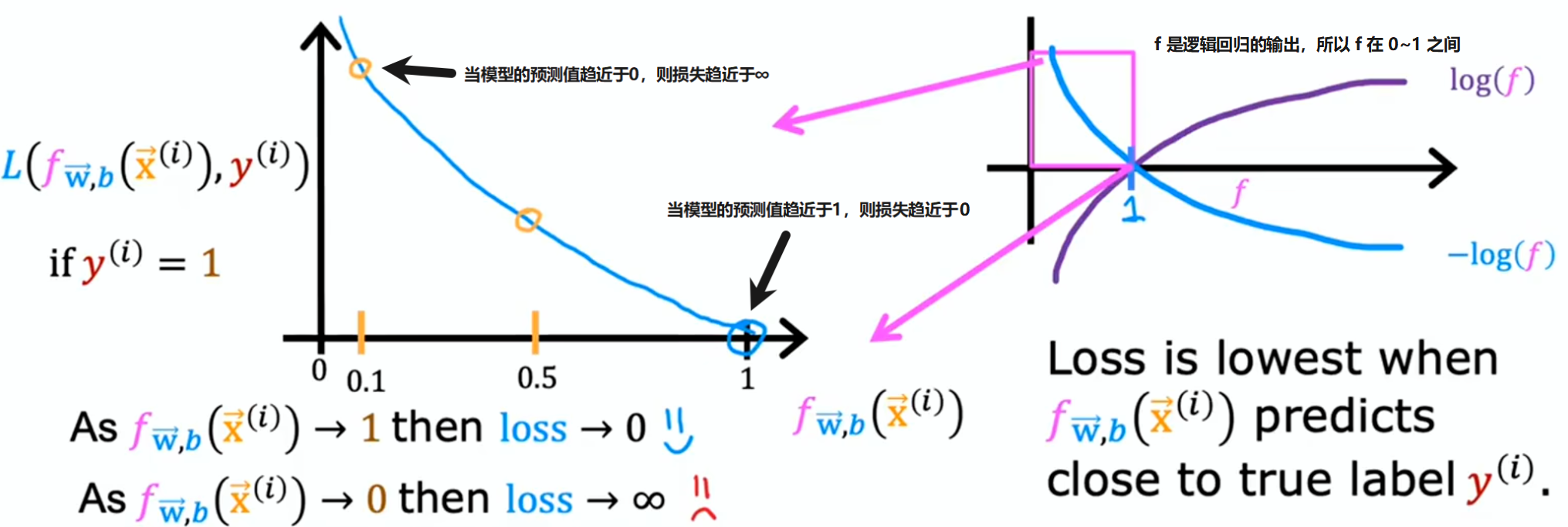
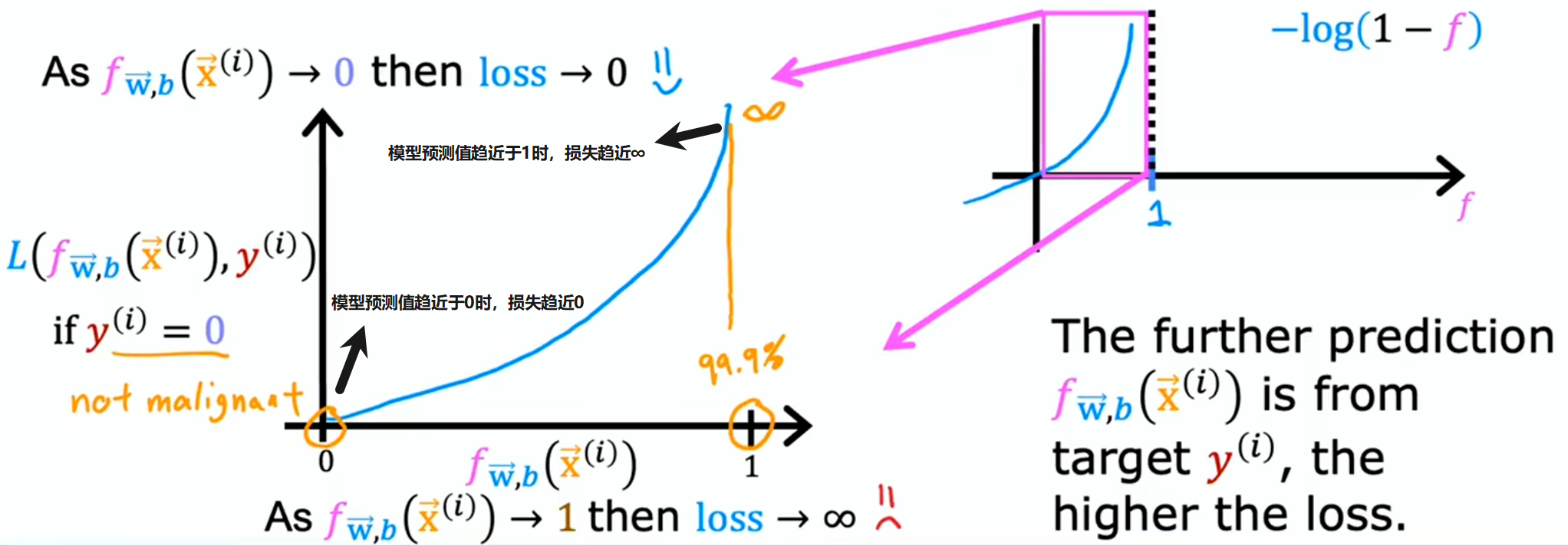
损失函数衡量的是单个样本上的表现情况，通过对所有训练样本的损失进行求和进而得到成本函数

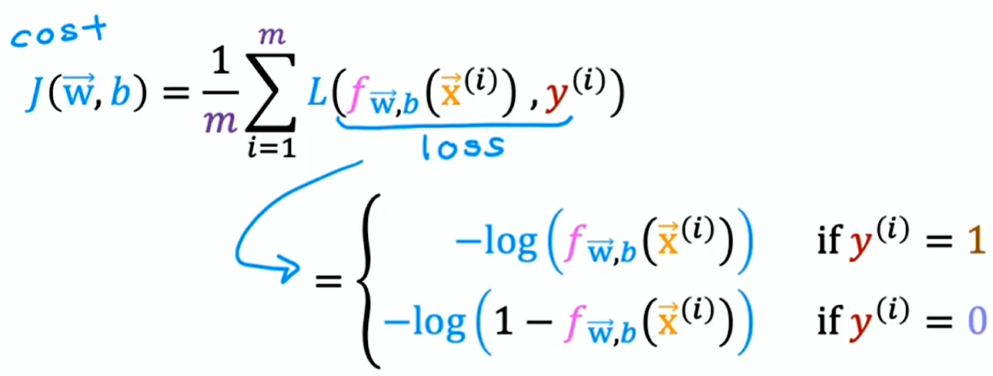
这个成本函数是凸函数，能够放心地用梯度下降法找到全局最小值

简化逻辑损失函数

对于上述的逻辑损失函数：

$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=\{\begin{array}{rc}-log(f_{\vec{w},b}({\vec{x}}^{(i)}))& if{y}^{(i)}=1\\ -log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))& if{y}^{(i)}=0\end{array}$$

由于 $y^{(i)}$ 只能取 0 或 1，可简化为：

$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=-y^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))$$

将 $y^{(i)}=0$ 和 $y^{(i)}=1$ 分别代入上式，即可发现两个公式完全等效

最终的成本函数（二元交叉熵函数）：

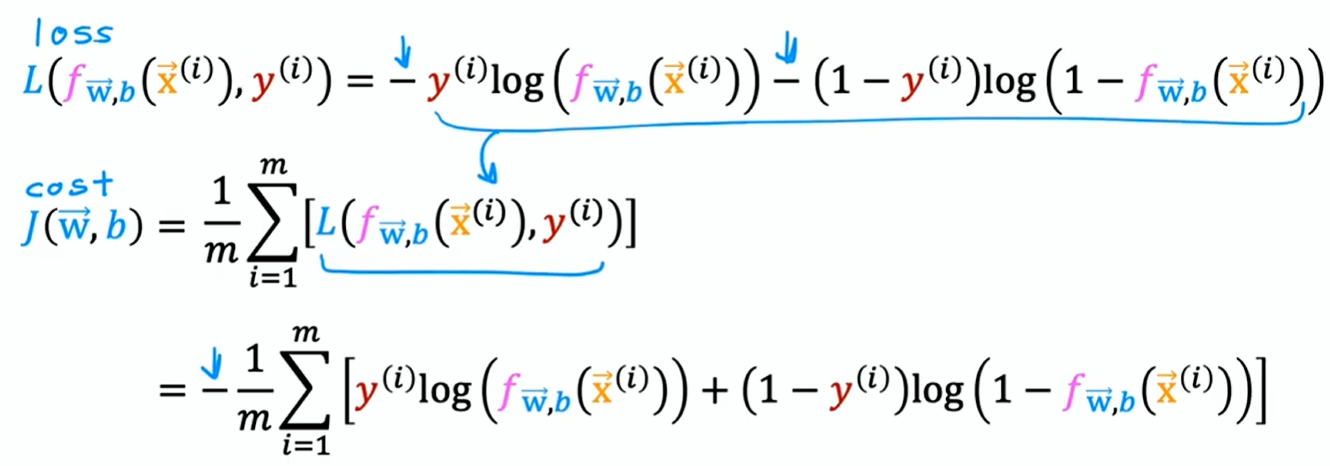
这个特定的成本函数是依据统计学中的最大似然估计原理推导而来的

梯度下降