007.自动求导

知识点

向量链式法则

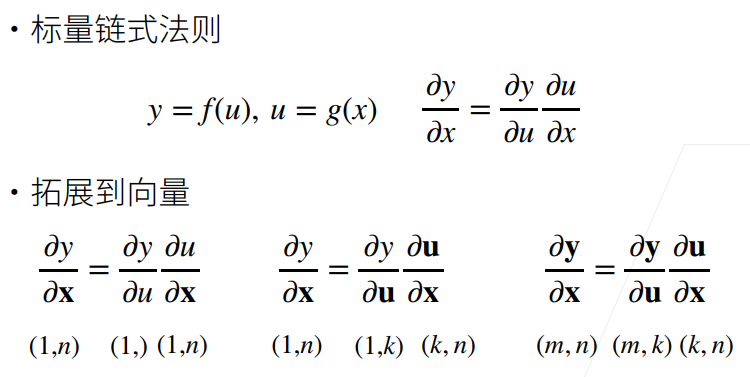
例 1：

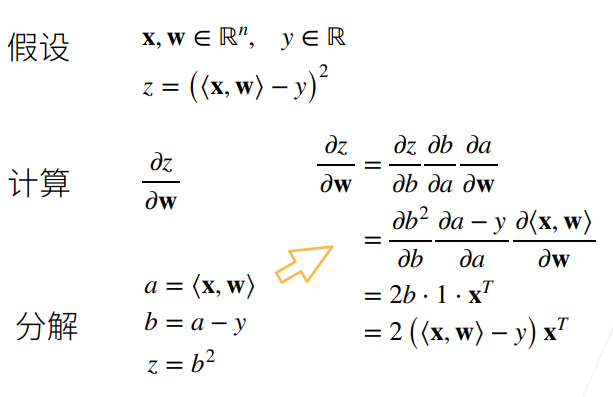
例 2：

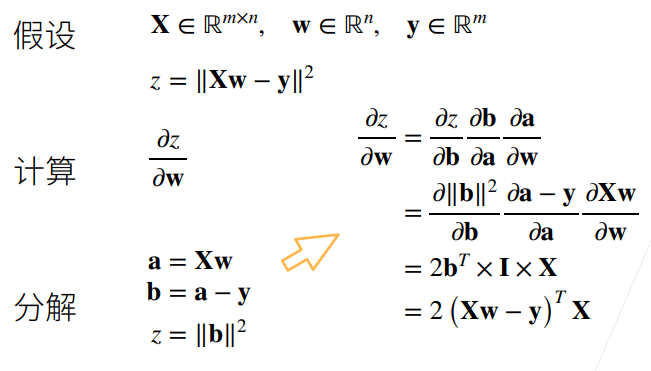
自动求导

自动求导计算一个函数在指定值上的导数

它有别于：

• 符号求导

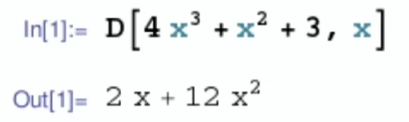
• 数值求导

$$\frac{\partial f(x)}{\partial x}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

计算图

自动求导的原理是计算图

• 将代码分解成操作子
• 将计算表示成一个无环图

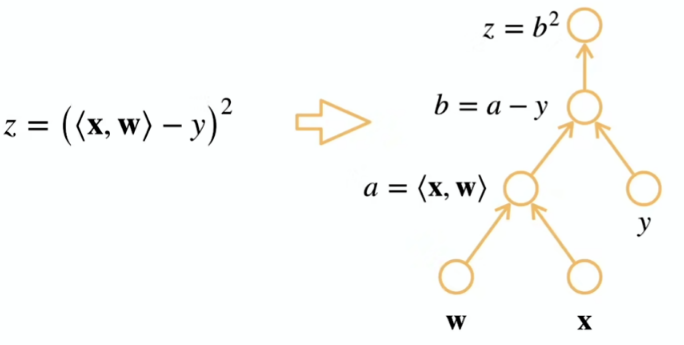
显式构造：Tensorflow/Theano/MXNet

from mxnet import sym
 
a = sym.var()
b = sym.var()
c = 2 * a + b
# 之后将数据绑定到 a 和 b 中

隐式构造：PyTorch/MXNet

from mxnet import autograd, nd
 
with autograd.record():
	a = nd.ones((2,1))
	b = nd.ones((2,1))
	c = 2 * a + b

自动求导的两种模式

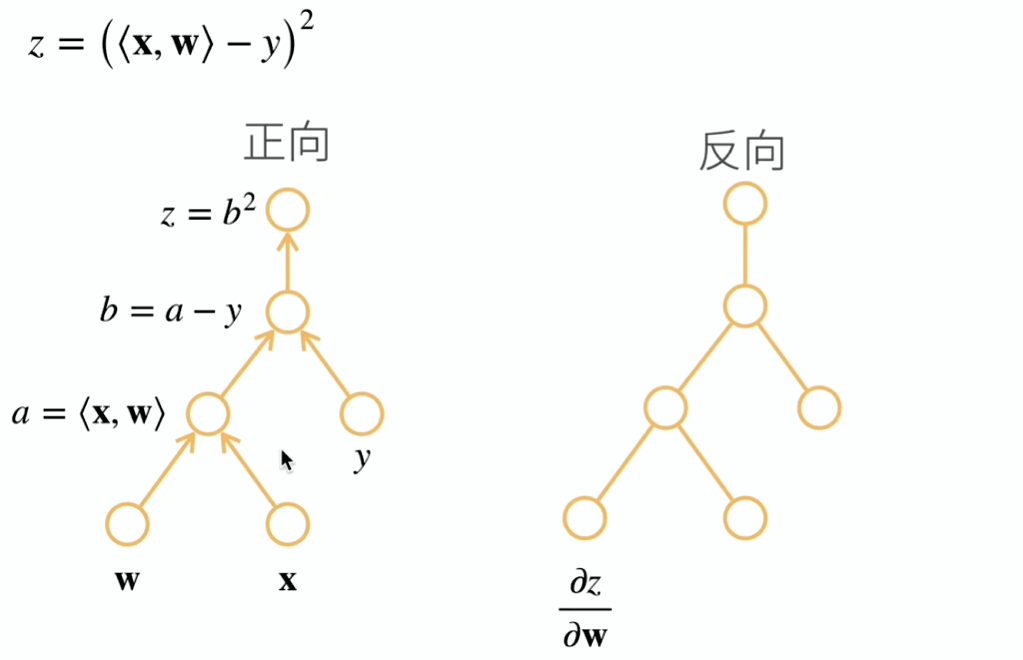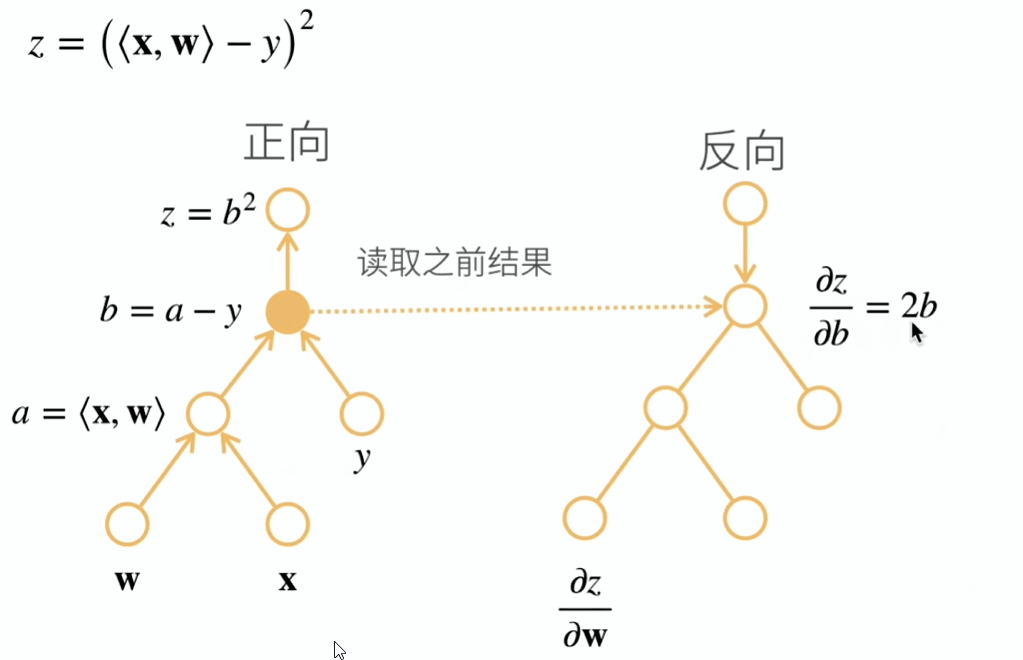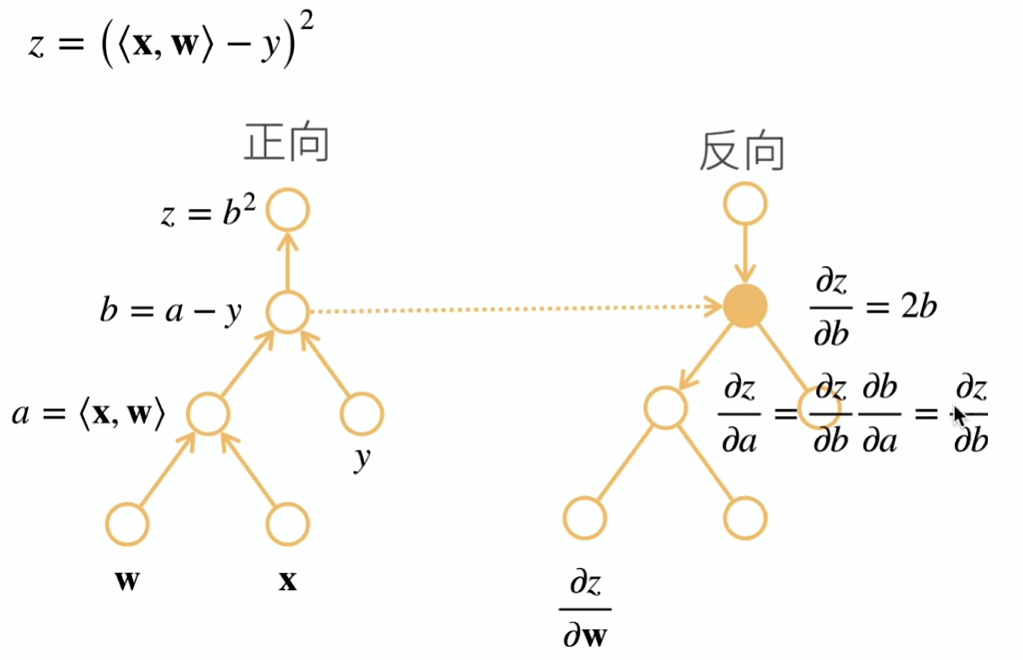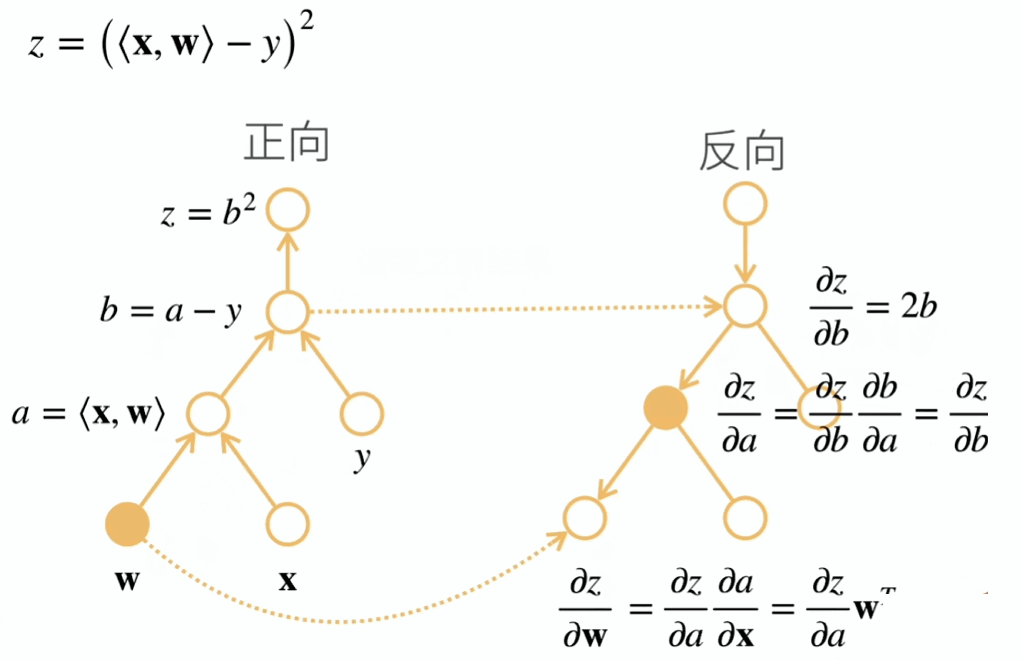
反向累积总结：

• 构造计算图
• 前向：执行图，存储中间结果
• 反向：从相反方向执行图
  • 去除不需要的枝

复杂度：

• 计算复杂度：O(n)，n 是操作子个数
  • 通常正向和方向的代价类似
• 内存复杂度：O(n)，因为需要存储正向的所有中间结果
• 跟正向累积对比：
  • O(n) 计算复杂度用来计算一个变量的梯度
  • O(1) 内存复杂度

代码

一个简单的例子

假设我们想对函数 $y=2{\mathbf{x}}^{\top }\mathbf{x}$ 关于列向量 $\mathbf{x}$ 求导

import torch
 
x = torch.arange(4.0)
x
'''
tensor([0., 1., 2., 3.])
'''

在计算 $y$ 关于 $\mathbf{x}$ 的梯度之前，需要一个地方来存储梯度

x.requires_grad_(True)  # 等价于 x = torch.arange(4.0, requires_grad=True)
x.grad  # 默认值是 None

现在计算 $y$

y = 2 * torch.dot(x, x)
y
'''
tensor(28., grad_fn=<MulBackward0>)
'''

通过调用反向传播函数来自动计算 y 关于 x 每个分量的梯度

y.backward()
x.grad
'''
tensor([ 0.,  4.,  8., 12.])
'''

现在计算 x 的另一个函数

# 在默认情况下，PyTorch 会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
'''
tensor([1., 1., 1., 1.])
'''

非标量变量的反向传播

深度学习中，我们的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和

# 对非标量调用 backward 需要传入一个 gradient 参数，该参数指定微分函数关于 self 的梯度
# 本例只想求偏导数的和，所以传递一个 1 的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于 y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad
'''
tensor([0., 2., 4., 6.])
'''

分离计算

将某些计算移动到记录的计算图之外

x.grad.zero_()
y = x * x
u = y.detach() # 把 y 当作一个常数，而不是关于 x 的函数
# y 是 x 的函数，但 u 不是
z = u * x
 
z.sum().backward()
x.grad == u
'''
tensor([True, True, True, True])
'''

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
'''
tensor([True, True, True, True])
'''

Python 控制流的梯度计算

即使构建函数的计算图需要通过 Python 控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度

def f(a):
	b = a * 2
	while b.norm() < 1000:
	    b = b * 2
	if b.sum() > 0:
	    c = b
	else:
	    c = 100 * b
	return c
 
# 计算梯度
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
a.grad == d / a
'''
tensor(True)
'''