线性回归
线性模型
- 给定 n 维输入:
- 线性模型有一个 n 维权重和一个标量偏差:
- 输出是输入的加权和:
- 向量版本:
衡量预估质量
比较真实值和预估值,例如房屋售价和估价
假设 是真实值, 是估计值,我们可以比较:
这个叫做平方损失
训练数据
收集一些数据点来决定参数值(权重和偏差),例如过去 6个月卖的房子,这被称之为训练数据,通常越多越好
假设我们有 n 个样本,记:
参数学习
训练损失:
最小化损失来学习参数:
显示解
将偏差加入权重:
损失是凸函数,所以最优解满足:
总结
- 线性回归是对 n 维输入的加权,外加偏差
- 使用平方损失来衡量预测值和真实值的差异
- 线性回归有显示解
- 线性回归可以看做是单层神经网络
基础优化算法
梯度下降
挑选一个初始值 ,重复迭代参数
- 沿梯度方向将增加损失函数值
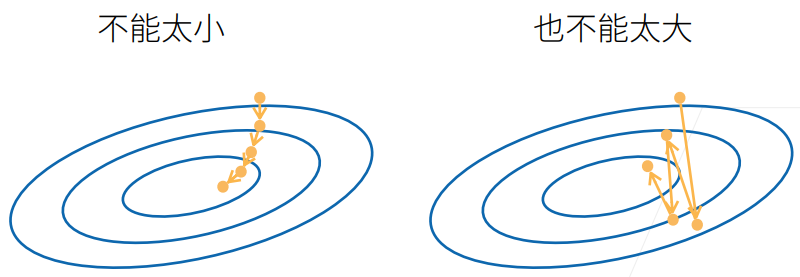
- 学习率 :步长的超参数
小批量随机梯度下降
在整个训练集上算梯度太贵,一个深度神经网络模型可能需要数分钟至数小时
我们可以随机采样 b 个样本 来近似损失:
- b 是批量大小,另一个重要的超参数
- 不能太小:每次计算量太小,不适合并行来最大利用计算资源
- 不能太大:内存消耗增加;浪费计算,例如如果所有样本都是相同的
总结
- 梯度下降通过不断沿着反梯度方向更新参数求解
- 小批量随机梯度下降是深度学习默认的求解算法
- 两个重要的超参数是批量大小和学习率