旋转位置编码由苏剑林大神设计，其引入数学中最美丽的公式-欧拉公式

大家可以关注他的博客《科学空间》，会学到很多东西

预备知识

为了看懂 RoPE，我们需要了解一些预备知识，包括：

欧拉公式
复数/复平面
三角函数的几个公式

在你深入大量公式之前，先要了解：

复平面和欧拉公式的引入，只是为了简化计算过程
欧拉公式经常在数学、物理和工程领域被如此广泛应用
整个证明过程，先考虑词向量为二维，再利用矩阵的特性轻松拓展到多维
在证明二维场景的时候，引入复平面，原因是可以这样可以使用欧拉公式获取漂亮的数学特性，来简化过程

旋转位置编码 RoPE

RoPE（Rotation Position Encoding，旋转位置编码）提出为了能利用上 token 之间的相对位置信息，假定 query 向量 $q_{m}$ 和 key 向量 $k_{n}$ 之间的内积操作可以被一个函数 $g$ 表示，该函数 g 的输入是词嵌入向量 $x_{m}$ ， $x_{n}$ 和它们之间的相对位置 $m - n$

⟨ f_{q} (x_{m}, m), f_{k} (x_{n}, n) ⟩ = g (x_{m}, x_{n}, m - n)

大胆假设，小心求证。现在我们的目标就是找到一个合适的函数 $g$ ，使得 $g (x_{m}, x_{n}, m - n)$ 能够捕捉到词向量之间的相对位置信息

RoPE 提出，在词向量是二维的情况下，将平面转化为复平面，如果我们按照如下的方式定义函数 $f$ ，则可以找到对应的 $g$ ：

f_{q} (x_{m}, m) f_{k} (x_{n}, n) g (x_{m}, x_{n}, m - n) = (W_{q} x_{m}) e^{im θ} = (W_{k} x_{n}) e^{in θ} = Re [(W_{q} x_{m}) (W_{k} x_{n})^{*} e^{i (m - n) θ}]

Re 指的是复数的实数部分，更近一步，我们可以将函数 $f$ 定义为：

f_{q} (x_{m}, m) = (cos m θ sin m θ - sin m θ cos m θ) (W_{q}^{(1, 1)} W_{q}^{(2, 1)} W_{q}^{(1, 2)} W_{q}^{(2, 2)}) (x_{m}^{(1)} x_{m}^{(2)}) = (cos m θ sin m θ - sin m θ cos m θ) (q_{m}^{(1)} q_{m}^{(2)})

这边，不就是原来的query矩阵乘上了一个旋转矩阵吗？也就是说，加上 $m$ 这个位置信息后，如果使用 RoPE 的设计方案，就相当于将原 query 矩阵进行了旋转。这就是旋转的由来

同理， $f_{K}$ 可以表示为：

f_{k} (x_{m}, m) = (cos m θ sin m θ - sin m θ cos m θ) (W_{k}^{(1, 1)} W_{k}^{(2, 1)} W_{k}^{(1, 2)} W_{k}^{(2, 2)}) (x_{m}^{(1)} x_{m}^{(2)}) = (cos m θ sin m θ - sin m θ cos m θ) (k_{m}^{(1)} k_{m}^{(2)})

那么，对应的 $g$ 函数就是：

g (x_{m}, x_{n}, m - n) = (q_{m}^{(1)} q_{m}^{(2)}) (cos ((m - n) θ) sin ((m - n) θ) - sin ((m - n) θ) cos ((m - n) θ)) (k_{n}^{(1)} k_{n}^{(2)})

从二维到多维

在二维场景下，我们引入了复平面，是为了使用欧拉公式获取漂亮的数学特性，来简化过程。但是在多维场景下，我们可以直接使用矩阵的特性，来简化过程。将 2 维的 RoPE 推广到多维的 RoPE，只需要将 2 维的 RoPE 的旋转矩阵 $R$ 替换为多维的旋转矩阵 $R$ 即可

f_{{q, k}} (x_{m}, m) = R_{Θ, m}^{d} W_{{q, k}} x_{m}

因为内积满足线性叠加性质，所以任意偶数维的 RoPE 都可以表示为二维情形拼接而成的形式：

即是在原来的 $q * k$ 矩阵的基础上，加上了一个旋转矩阵 $R_{θ, m}^{d}$ ，这就是 RoPE 的设计思路

在原始 paper 中，有一个直观的图：

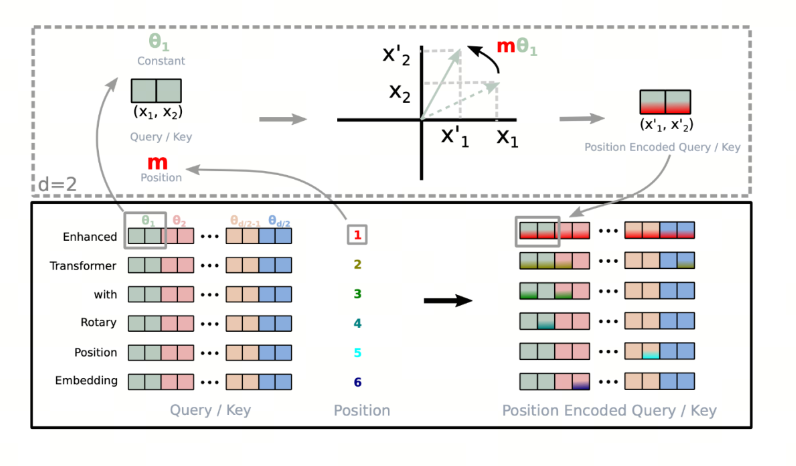
RoPE 的证明

注意，现在的证明是建立在二维的基础上，二维可以用上一节的矩阵特性推广到多维

二维的情况下，形式上我们将其转化为复平面

按照 RoPE 的设计，编码后的 $q, v$ 和内积 $< q, v >$ 的形式是：

f_{q} (x_{m}, m) f_{k} (x_{n}, n) g (x_{m}, x_{n}, m - n) = (W_{q} x_{m}) e^{im θ} = (W_{k} x_{n}) e^{in θ} = Re [(W_{q} x_{m}) (W_{k} x_{n})^{*} e^{i (m - n) θ}]

为什么上述公式满足：

⟨ f_{q} (x_{m}, m), f_{k} (x_{n}, n) ⟩ = g (x_{m}, x_{n}, m - n)

首先，我们看到欧拉公式：

e^{i x} = cos (x) + i sin (x)

则有：

e^{im θ} e^{in θ} e^{i (m - n) θ} = cos (m θ) + i s in (m θ) = cos (n θ) + i s in (n θ) = cos ((m - n) θ) + i s in ((m - n) θ)

我们看 query 矩阵，可以看到：

f_{q} (x_{m}, m) = (W_{q} x_{m}) e^{im θ}

其中 $W_{q}$ 是二维矩阵， $x_{m}$ 是二维向量，其乘积是一个二维向量，这边我们用 $q_{m}$ 表示。 $q_{m}^{(1)}$ , $q_{m}^{(2)}$ 分别表示第一维和第二维

q_{m} = (q_{m}^{(1)} q_{m}^{(2)}) = W_{q} x_{m} = (W_{q}^{(11)} W_{q}^{(21)} W_{q}^{(12)} W_{q}^{(22)}) (x_{m}^{(1)} x_{m}^{(2)})

我们这时，需要将 $q_{m}$ 转化为复数形式，即将这个二维平面放到复平面上，复平面的实部是第一维（x 轴），虚部是第二维（y 轴）

q_{m} = [q_{m}^{(1)}, q_{m}^{(2)}] = [q_{m}^{(1)} + i q_{m}^{(2)}]

这时，我们可以将 $f_{q} (x_{m}, m)$ 表示为：

f_{q} (x_{m}, m) = (W_{q} x_{m}) e^{im θ} = q_{m} e^{im θ}

这就是两个复数的积（将复数带入）

q_{m} e^{im θ} = (q_{m}^{(1)} + q_{m}^{(2)}) * (cos (m θ) + i s in (m θ))

经过简单的展开：

q_{m} e^{im θ} = (q_{m}^{(1)} + q_{m}^{(2)}) * (cos (m θ) + i s in (m θ)) = (q_{m}^{(1)} cos (m θ) - q_{m}^{(2)} s in (m θ)) + i (q_{m}^{(2)} cos (m θ) + q_{m}^{(1)} s in (m θ))

再重新从复平面回到实数二维平面，我们可以将上述公式表示为：

q_{m} e^{im θ} = [q_{m}^{(1)} cos (m θ) - q_{m}^{(2)} s in (m θ), q_{m}^{(2)} cos (m θ) + q_{m}^{(1)} s in (m θ)]

事实上这就是没有位置信息的 query 向量乘上了一个旋转矩阵，这就是 RoPE 的设计思路

f_{q} (x_{m}, m) = (W_{q} x_{m}) e^{im θ} = q_{m} e^{im θ} = [q_{m}^{(1)} cos (m θ) - q_{m}^{(2)} s in (m θ), q_{m}^{(2)} cos (m θ) + q_{m}^{(1)} s in (m θ)] = (cos m θ sin m θ - sin m θ cos m θ) (q_{m}^{(1)} q_{m}^{(2)})

同理，我们可以得到 key 向量的 RoPE 形式：

f_{k} (x_{n}, n) = (W_{k} x_{n}) e^{in θ} = k_{n} e^{in θ} = [k_{n}^{(1)} cos (n θ) - k_{n}^{(2)} s in (n θ), k_{n}^{(2)} cos (n θ) - k_{n}^{(1)} s in (n θ)] = (cos n θ sin n θ - sin n θ cos n θ) (k_{n}^{(1)} k_{n}^{(2)})

最后，我们可以得到 RoPE 的内积形式：

⟨ f_{q} (x_{m}, m), f_{k} (x_{n}, n) ⟩ = ((cos (m θ) sin (m θ) - sin (m θ) cos (m θ)) (q_{m}^{(1)} q_{m}^{(2)}))^{T} ((cos (n θ) sin (n θ) - sin (n θ) cos (n θ)) (k_{n}^{(1)} k_{n}^{(2)})) = (q_{m}^{(1)} q_{m}^{(2)}) (cos (m θ) - sin (m θ) sin (m θ) cos (m θ)) (cos (n θ) sin (n θ) - sin (n θ) cos (n θ)) (k_{n}^{(1)} k_{n}^{(2)}) = (q_{m}^{(1)} q_{m}^{(2)}) (cos (m θ) cos (n θ) + sin (m θ) sin (n θ) - sin (m θ) cos (n θ) + cos (m θ) sin (n θ) - cos (m θ) sin (n θ) + sin (m θ) cos (n θ) sin (m θ) sin (n θ) + cos (m θ) cos (n θ)) (k_{n}^{(1)} k_{n}^{(2)}) = (q_{m}^{(1)} q_{m}^{(2)}) (cos ((m - n) θ) sin ((m - n) θ) - sin ((m - n) θ) cos ((m - n) θ)) (k_{n}^{(1)} k_{n}^{(2)})

附录 1：复变函数

什么是复数

复数是数学中的一个基本概念，它扩展了实数系统，允许进行更广泛的数学运算。复数由两部分组成：实部和虚部。复数的一般形式可以表示为：

a + bi

其中， a 是复数的实部， b 是复数的虚部，而 i 是虚数单位，满足 $i^{2} = - 1$

复数的两个主要特征是：

实数：当虚部 b 为 0 时，复数退化为实数
虚数：当实部 a 为 0 且虚部 b 非零时，复数被称为纯虚数

复数可以进行加、减、乘、除等基本算术运算，这些运算遵循特定的规则。例如，两个复数的加法运算是将它们的实部和虚部分别相加：

(a + bi) + (c + d i) = (a + c) + (b + d) i

复数的乘法运算则稍微复杂一些，需要用到分配律和虚数单位 i 的性质：

(a + bi) (c + d i) = a c + a d i + b c i + b d i^{2} = (a c - b d) + (a d + b c) i

复数的除法运算涉及到将分母实数化，通常通过乘以共轭复数来实现

复数在数学、物理、工程学等领域有着广泛的应用，如在信号处理、量子力学、电气工程等学科中，复数提供了一种描述周期性现象和旋转的有力工具

复变函数

复变函数是数学中的一个重要分支，它主要研究复数域上的函数，这些函数的自变量和因变量都是复数。复变函数论在许多工程和科学领域都有应用，以下是一些通常会学习复变函数的专业：

数学专业：复变函数是数学专业学生的必修课程之一，因为它是数学分析的延伸和深化
电气工程：在信号处理和系统分析中，复变函数用于分析交流电路
电子工程：在控制系统的设计和分析中使用复数域方法
物理学专业：在量子力学和电磁学中，复变函数理论用于解决波动方程和势问题
计算机科学与工程：在算法设计、图像处理和信号处理的算法开发中，复变函数有其应用
航空航天工程：在流体动力学和控制系统分析中，复变函数用于数学建模
机械工程：在振动分析和热传导问题中，复变函数理论有助于找到解决方案
土木工程：在结构分析和地震工程中，复变函数用于解决某些动态问题
生物学和生物医学工程：在生物信号处理和生物物理建模中，复变函数有助于分析和理解生物系统的动态行为
金融数学和经济学：在某些高级经济模型和金融工具定价中，复变函数理论可以提供分析工具
控制理论：在系统稳定性分析和控制器设计中，复变函数是基本工具之一

学习复变函数的课程通常包括解析函数、复积分、级数展开、留数定理、共轭和谐函数等概念

复数在机器学习中的应用相对较少，但在某些特定领域，如信号处理、图像处理和模式识别中，复数的性质和运算规则可以提供一些有用的工具和技术

毕业十年后，我再一次领略了复数的魅力，这次是在大模型的位置编码中。复数的数学特性和运算规则为 Transformer 提供了一种新的位置编码方法，这种方法被称为 RoPE（Rotary Position Embedding）

附录 2：欧拉公式

导入

也许你在某些场合听说过欧拉公式，也许你干脆对数学不感冒。机缘巧合下，你点开了这篇文章，大致浏览了下然后关闭，继续为自己的工作学习忙碌。这不妨碍你暂停忙碌的脚步，欣赏她的美

若干年后，你应该不曾记得看过这篇文章，但你会记得数学界有一个很美的公式

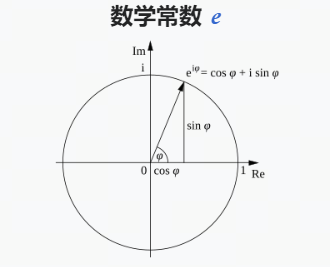
欧拉公式

欧拉公式（Euler’s formula）是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名。欧拉公式提出，对任意实数 x，都存在：

e^{i x} = cos (x) + i sin (x)

其中 e 是自然对数的底数，i 是虚数单位，而 cos 和 sin 则是余弦、正弦对应的三角函数，参数 x 则以弧度为单位

这是一个非常美丽的公式，它将三角函数，指数函数，复数联系在了一起，是数学中的一颗明珠

欧拉恒等式

欧拉恒等式（Euler’s identity）是欧拉公式的一个特例，当 $x = π$ 时，欧拉公式变为：

e^{iπ} + 1 = 0

这个公式被认为是数学中最美丽的公式之一，它将五个最重要的数学常数联系在了一起：0、1、e、i 和 π

欧拉的贡献

莱昂哈德·欧拉（1707 年 4 月 15 日——1783 年 9 月 18 日），瑞士数学家、物理学家、天文学家、地理学家、逻辑学家和工程师。近代数学先驱之一

欧拉在包括微积分和图论在内的多个数学领域都做出过重大贡献。他引进和推广了许多数学术语和书写格式，并一直沿用至今，例如：

函数的记法 $f (x)$
虚数单位 $- 1$ 的记法 $i$
圆周率的记法 $π$
求和符号 $Σ$
差分符号 $Δ$
用小写字母表示三角形的边；用大写字母表示三角形的角等
给出了自然对数的底数 $e$ 定义，其也称为欧拉数（Euler’s number）
此外，他还在力学、流体动力学、光学、天文学和乐理领域有突出的贡献

欧拉是 18 世纪杰出的数学家，同时也是有史以来最伟大的数学家之一。他也是一位多产作者，其学术著作有 60-80 册

欧拉逝世后，几位著名的数学家高度评价他对数学的贡献，例如法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献：“读欧拉的著作吧，在任何意义上，他都是我们的大师”

德国数学家卡尔·弗里德里希·高斯曾写道：“对欧拉所有的著作的研究将永远是数学各个领域最好的学习之所，没有任何其他东西可以取代它”

莱昂哈德·欧拉 - wiki

总结

RoPE 非常巧妙的借助复平面和欧拉公式，将位置信息编码到了 query 和 key 向量中，使得模型能够利用上 token 之间的相对位置信息。RoPE 的设计思路是将 query 和 key 向量进行旋转，这就是旋转的由来

My-Notes

全部文章

002.旋转位置编码