014.Sigmiod、Softmax、Tanh

本文介绍三个古早的激活函数，虽然古老，但是在神经网络中仍然有着广泛的应用，尤其是 Softmax 作为输出层，仍然是统治地位

Sigmoid 函数

Sigmoid 函数的概念可以追溯到 19 世纪，但在现代科学和工程中，它的广泛应用主要是从 20 世纪中期开始的

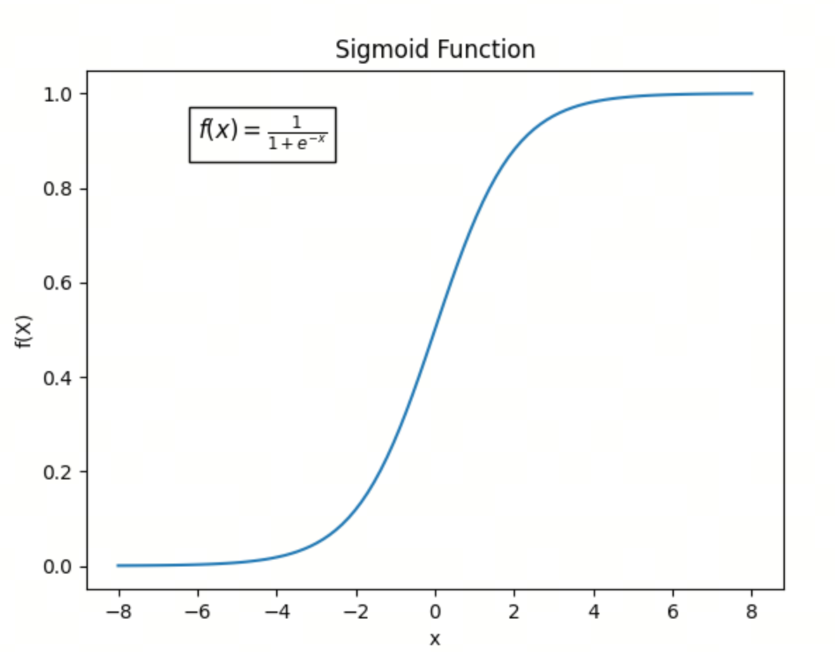
定义

Sigmoid 函数的数学形式为：

$$\sigma (x)=\frac{1}{1+e^{-x}}$$

关键性质

1. 输出范围：输出值始终在 $(0,1)$ 区间内，这使得 Sigmoid 函数在输出概率或者用于二分类问题时非常有用
2. 平滑连续：Sigmoid 函数在整个定义域内都是光滑且连续的，这有助于在优化过程中计算梯度
3. 中心对称：Sigmoid 函数关于直线 $y=x$ 对称，这意味着它能够处理正负输入值
4. 梯度问题：当输入值 $x$ 非常大或非常小的时候，Sigmoid 函数的梯度接近于 0，这可能导致梯度消失问题，从而使得在神经网络的深层中梯度难以传播
5. 非零中心：Sigmoid 函数的输出不是以 0 为中心的，这可能会导致网络在优化过程中花费更多的时间和资源来调整权重

历史背景

1. 早期数学背景：
   • Sigmoid 函数的数学形式与累积分布函数（CDF）有相似之处。早在 19 世纪，数学家们就研究了类似的函数形式，特别是在概率和统计学中
2. 生物学和神经科学中的应用：
   • 在 20 世纪中期，生物学家和神经科学家开始使用 Sigmoid 函数来描述神经元的激活函数。特别是，神经科学家 Warren McCulloch 和 Walter Pitts 在 1943 年提出的 McCulloch-Pitts 神经元模型中，使用了类似于 Sigmoid 函数的激活函数
3. 人工神经网络中的应用：
   • 在 20 世纪 80 年代，随着人工神经网络的兴起，Sigmoid 函数成为一种标准的激活函数。特别是在多层感知器（MLP）和反向传播算法（由 David Rumelhart、Geoffrey Hinton 和 Ronald Williams 在 1986 年提出）中，Sigmoid 函数被广泛使用，因为它的导数形式简单，便于计算梯度

应用

• 二分类：在二分类问题的输出层，Sigmoid 函数可以将输出转换为概率值，用于表示属于某一类的概率
• 逻辑回归：在逻辑回归模型中，Sigmoid 函数用于将线性回归的输出转换为概率预测
• 隐藏层：虽然在现代深度学习模型中较少用于隐藏层，但在某些情况下，Sigmoid 仍然可以作为隐藏层的激活函数

局限性

• 梯度消失：在深层网络中，由于 Sigmoid 函数在输入值绝对值较大时梯度接近于 0，容易导致梯度消失问题，从而阻碍深层网络的训练
• 计算开销：相比于某些激活函数（如 ReLU），Sigmoid 函数的计算复杂度较高，因为它涉及到指数运算

由于这些局限性，Sigmoid 函数在现代深度学习模型中逐渐被其他激活函数（如 ReLU 及其变种）所取代，尤其是在隐藏层中。然而，在需要输出概率预测的特定场景下，Sigmoid 函数仍然是一种重要的激活函数

示例

以下是一个简单的 Python 示例，展示如何计算 Sigmoid 函数：

import numpy as np
 
def sigmoid(x):
    """Sigmoid 激活函数
 
    参数:
    x -- 输入值
 
    返回:
    Sigmoid 激活后的值
    """
    return 1 / (1 + np.exp(-x))

Softmax 函数

Softmax 函数是一种广泛应用于机器学习和深度学习中的激活函数，特别是在多分类任务中。它将一个包含任意实数的向量转换为一个概率分布。Softmax 函数的提出和应用与统计力学和信息理论中的概念有关

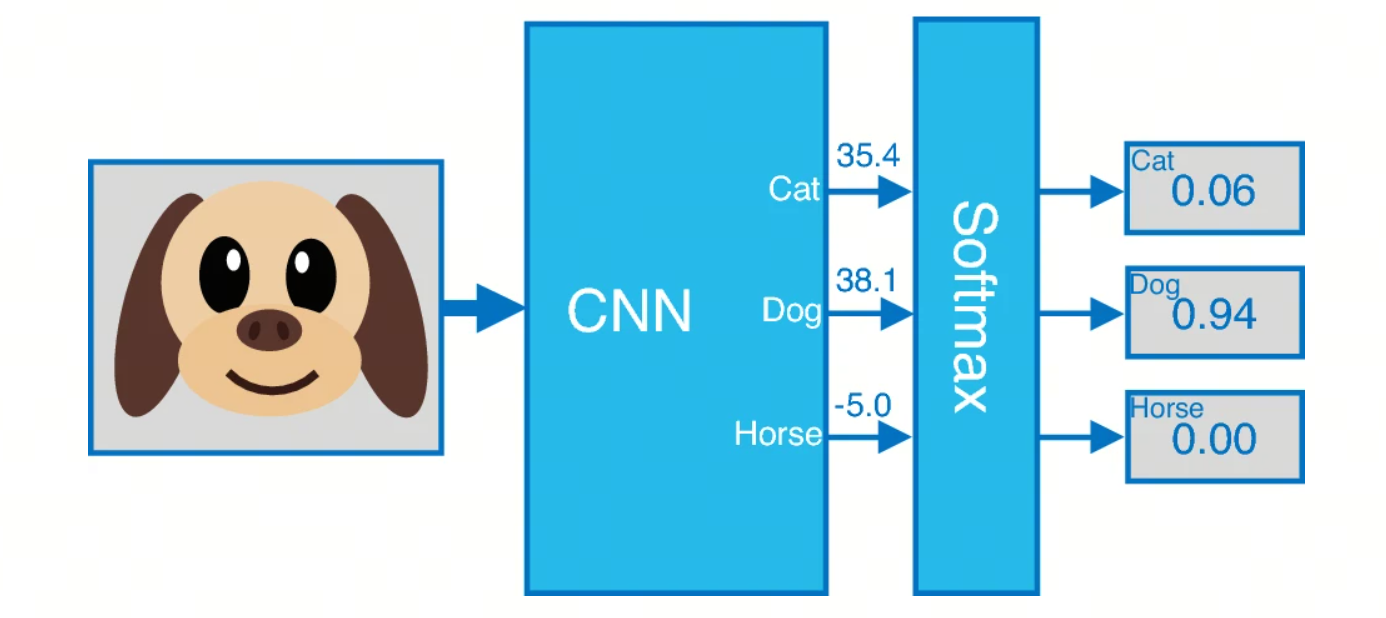
定义

给定一个包含 $n$ 个实数的向量 $\mathbf{z}=[z_1,z_2,\dots ,z_n]$，Softmax 函数将其转换为一个概率分布 $\mathbf{p}=[p_1,p_2,\dots ,p_n]$，其中每个 $p_i$ 的计算公式为：

$$p_i=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$

关键性质

1. 非负性：对于任意 $i$， $p_i\ge 0$
2. 归一化：所有输出的和为 1，即 ${\sum }_{i=1}^n{p}_i=1$
3. 指数函数的使用：指数函数 $e^{z_i}$ 确保了输出值为正，并且放大了较大的 $z_i$ 值的差异

历史背景

Softmax 函数的概念来源于统计力学中的 Boltzmann 分布（也称为 Gibbs 分布），它描述了系统在热平衡状态下不同能量状态的概率分布。这个概念在信息理论和机器学习中得到了广泛应用

1. 统计力学：在 19 世纪末和 20 世纪初，Ludwig Boltzmann 和 Josiah Willard Gibbs 等科学家研究了热力学系统的能量分布，提出了 Boltzmann 分布
2. 信息理论：20 世纪中期，Claude Shannon 的工作奠定了信息理论的基础，其中包括熵和信息量的概念，这些概念与概率分布密切相关
3. 机器学习：在 20 世纪后期，特别是随着神经网络和深度学习的兴起，Softmax 函数被引入到多分类问题中，用于输出层的激活函数，以将网络的输出转换为概率分布

应用

多分类问题：Softmax 函数常用于神经网络的输出层，在多分类问题中将网络的输出转换为类别的概率分布

示例

假设有一个包含三个元素的向量 $\mathbf{z}=[2.0,1.0,0.1]$，则 Softmax 函数的输出为：

import numpy as np
 
z = np.array([2.0, 1.0, 0.1])
softmax = np.exp(z) / np.sum(np.exp(z))
 
print(softmax)

输出：

[0.65900114 0.24243297 0.09856589]

这表示第一个元素的概率最大，约为 0.659，第二个元素的概率约为 0.242，第三个元素的概率最小，约为 0.099

Tanh 函数

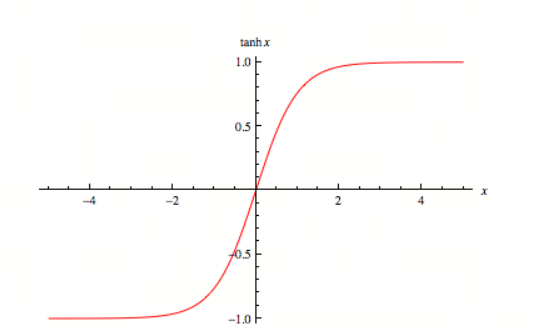
定义

Tanh 函数（双曲正切函数）是一个常见的激活函数，广泛应用于神经网络和机器学习中。它的数学表达式为：

$\text{tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

Tanh 函数的导数可以表示为：

$\frac{d}{dx}\text{tanh}(x)=1-{\text{tanh}}^2(x)$

这意味着在输入值接近 $-1$ 或 $1$ 时，导数值接近 0，而在输入值接近 0 时，导数值接近 1

关键性质

1. 输出范围：Tanh 函数的输出值在 $-1$ 到 $1$ 之间
2. 中心对称性：Tanh 函数是关于原点对称的，即 $\text{tanh}(-x)=-\text{tanh}(x)$
3. 平滑性：Tanh 函数是一个平滑的、连续的函数，具有良好的导数性质

历史背景

Tanh 函数与双曲函数的研究可以追溯到 18 世纪。它在数学和工程学中有广泛的应用，特别是在信号处理和控制系统中。随着神经网络的发展，Tanh 函数被引入作为一种激活函数

应用

在神经网络中，Tanh 函数常用于隐藏层的激活函数。它的输出范围在 $-1$ 到 $1$ 之间，这使得它在某些情况下比 Sigmoid 函数更有优势，因为它的输出是零中心的，有助于加速梯度下降的收敛

总结

今天介绍了三个古老的激活函数，它们在神经网络中仍然有着广泛的应用

• Sigmoid 函数作为一种非线性函数，可以引入非线性变换，增加神经网络的表达能力
• Softmax 函数常用于多分类问题，将网络的输出转换为类别的概率分布
• Tanh 函数作为隐藏层的激活函数，输出范围在 $-1$ 到 $1$ 之间，有助于加速梯度下降的收敛