016.ELU 及其变种 SELU

ELU（Exponential Linear Unit，指数线性单元）激活函数是为了进一步改进 ReLU 及其变体（如 Leaky ReLU 和 PReLU）的性能而提出的。ELU 旨在解决 ReLU 的一些固有问题，特别是负区间的特性和输出均值的偏移

ELU 函数

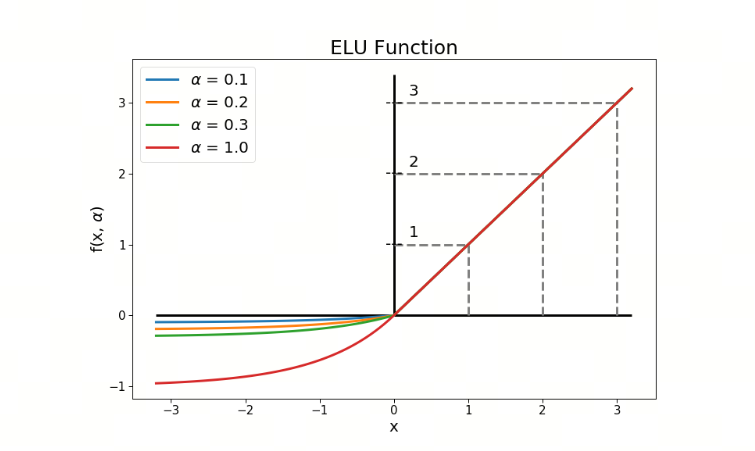
ELU 通过在负区间引入指数函数来改进 ReLU 及其变体的性能。ELU 旨在解决 ReLU 的一些固有问题，如 Dying ReLU 问题和输出均值偏移问题

数学定义

ELU 的数学表达式为：

$$\text{ELU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha (e^x-1)& \text{if }x<0\end{array}$$

其中，$\alpha$ 是一个超参数，通常取值为 1

关键性质

1. 非线性：与 ReLU 一样，ELU 引入了非线性特性，使得神经网络能够学习复杂的模式
2. 避免 Dying ReLU 问题：通过在负区间引入指数函数，ELU 确保了所有神经元都有梯度，从而有效地避免了 Dying ReLU 问题
3. 输出均值接近零：ELU 的负区间输出为 $\alpha (e^x-1)$，这使得其输出均值更接近于零，从而有助于加速神经网络的学习过程。相比之下，ReLU 在负区间的输出为零，这可能导致输出均值偏移
4. 平滑性：ELU 在负区间的输出是连续且光滑的，这有助于提高模型的稳定性和收敛速度

提出时间

ELU 激活函数是在 2015 年由 Djork-Arné Clevert、Thomas Unterthiner 和 Sepp Hochreiter 在论文《Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)》中提出的

应用

ELU 在许多深度学习模型中得到了应用，特别是在卷积神经网络（CNN）和其他需要处理大量非线性数据的模型中。它通过改进负区间的特性和输出均值，使得模型能够更快地收敛并达到更高的性能

SELU 函数

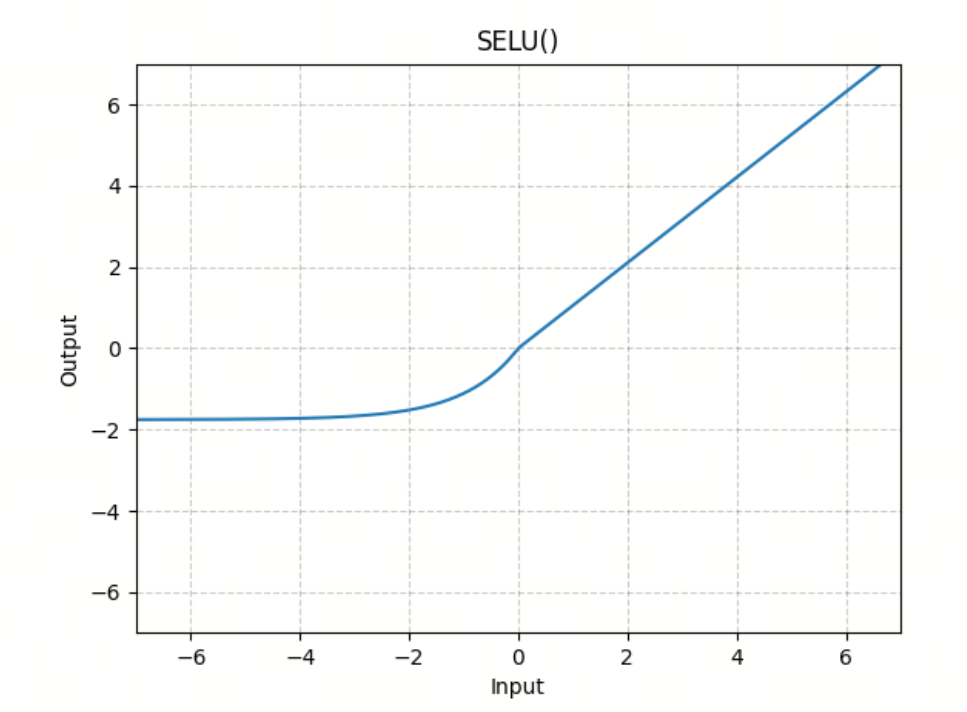
SELU（Scaled Exponential Linear Unit，缩放指数线性单元）激活函数是 ELU 的一个变体，通过引入缩放因子来进一步改进神经网络的性能。SELU 不仅解决了 ReLU 的一些问题，还引入了自归一化（self-normalizing）的特性，使得神经网络在训练过程中能够自动保持均值和方差的稳定

数学定义

SELU 的数学表达式为：

$$\text{SELU}(x)=\lambda \{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha (e^x-1)& \text{if }x<0\end{array}$$

其中，$\alpha$ 和 $\lambda$ 是两个固定的参数，通常取值为：

• $\alpha \approx 1.67326$
• $\lambda \approx 1.0507$

关键性质

1. 非线性：与 ReLU 和 ELU 一样，SELU 引入了非线性特性，使得神经网络能够学习复杂的模式
2. 避免 Dying ReLU 问题：通过在负区间引入指数函数，SELU 确保了所有神经元都有梯度，从而有效地避免了 Dying ReLU 问题
3. 自归一化：SELU 的一个重要特性是其自归一化特性，即在每一层的输出均值和方差能够自动趋于稳定。这有助于加速训练过程并提高模型的性能
4. 输出均值和方差稳定：SELU 的缩放因子 $\lambda$ 和 $\alpha$ 的选择，使得其输出均值和方差能够保持稳定，从而有助于防止梯度消失和梯度爆炸问题

提出时间

SELU 激活函数是在 2017 年由 Günter Klambauer、Thomas Unterthiner、Andreas Mayr 和 Sepp Hochreiter 在论文《Self-Normalizing Neural Networks》中提出的