018.GELU、Mish

GELU

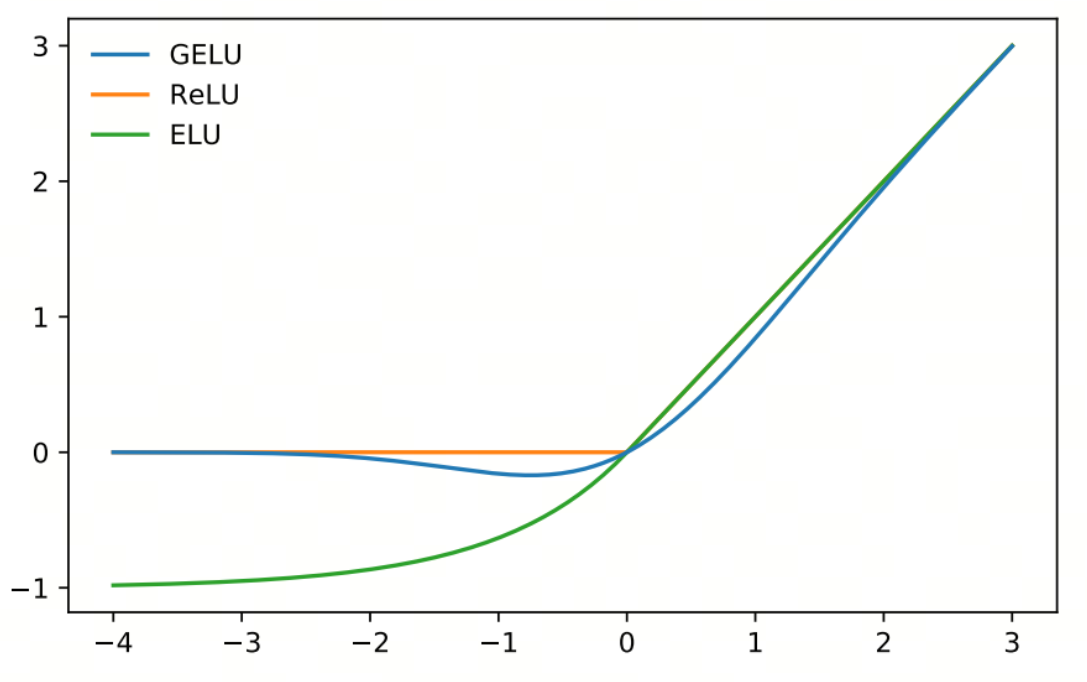
GELU（Gaussian Error Linear Unit，高斯误差线性单元）是一种在深度学习中广泛应用的激活函数。GELU 通过高斯误差函数（即标准正态分布的累积分布函数）对输入进行平滑处理，从而提高模型的性能。GELU 在许多任务中表现出色，特别是在自然语言处理（NLP）和计算机视觉任务中

数学定义

GELU 函数的数学表达式为：

$$\text{GELU}(x)=x\cdot \Phi (x)$$

其中：

• $x$ 是输入
• $\Phi (x)$ 是标准正态分布的累积分布函数
  • 定义为：$\Phi (x)=\frac{1}{2}\left(1+\text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)$
  • 其中，$\text{erf}(x)$ 是误差函数

近似表达式

为了简化计算，GELU 函数通常采用以下近似表达式：

$$\text{GELU}(x)\approx 0.5\cdot x\cdot \left(1+\tanh \left(\sqrt{\frac{2}{\pi }}\left(x+0.044715x^3\right)\right)\right)$$

这种近似计算在实际应用中非常常见，因为它计算效率更高

关键性质

1. 平滑性：GELU 函数是连续且平滑的，这有助于提高模型的稳定性和收敛速度
2. 非线性：GELU 结合了线性和非线性变换，使得模型能够学习复杂的模式
3. 概率解释：GELU 通过高斯误差函数对输入进行平滑处理，从而具有概率解释，即输入值越大，通过的概率越高

提出时间

GELU 激活函数是在 2016 年由 Dan Hendrycks 和 Kevin Gimpel 在论文《Gaussian Error Linear Units (GELUs)》中提出的。

解决的问题

1. 平滑激活：GELU 通过引入高斯误差函数，使得激活函数在输入的正负区间内都具有平滑性，从而提高模型的稳定性
2. 非线性增强：GELU 结合了线性变换和非线性激活，从而增强了模型的非线性特性
3. 概率解释：GELU 具有概率解释，使得输入值越大，通过的概率越高，从而更好地模拟神经元的激活过程

示例

以下是一个简单的 Python 示例，展示如何计算 GELU 函数：

from scipy.special import erf
 
# 定义 GELU 函数
def gelu(x):
    return 0.5 * x * (1 + erf(x / np.sqrt(2)))

Mish

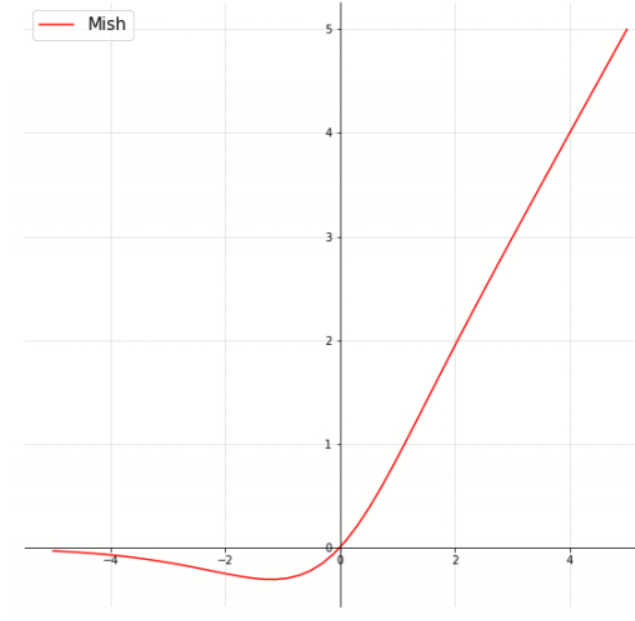
Mish 激活函数是一种在深度学习中使用的非线性激活函数，由 Diganta Misra 在 2019 年提出。Mish 激活函数通过平滑的非线性变换来增强模型的性能，并且在许多任务中表现出色，包括计算机视觉和自然语言处理

数学定义

Mish 激活函数的数学表达式为：

$$\text{Mish}(x)=x\cdot \tanh (\text{softplus}(x))$$

其中：

• $\text{softplus}(x)=\ln (1+e^x)$ 是 Softplus 函数
• $\tanh (x)$ 是双曲正切函数

关键性质

1. 平滑性：Mish 函数是连续且平滑的，这有助于提高模型的稳定性和收敛速度
2. 非单调性：Mish 函数是非单调的，这意味着它在某些区间内是递增的，而在其他区间内是递减的。这种特性使得 Mish 能够捕捉到更复杂的模式
3. 无界性：与 ReLU 不同，Mish 函数在负值区域是无界的，这有助于梯度流动，避免梯度消失问题
4. 近似 ReLU：当输入值较大时，Mish 函数近似于 ReLU 函数

提出时间

Mish 激活函数是在 2019 年由 Diganta Misra 在论文《Mish: A Self Regularized Non-Monotonic Neural Activation Function》中提出的

解决的问题

1. 平滑激活：Mish 通过引入 Softplus 和双曲正切函数，使得激活函数在输入的正负区间内都具有平滑性，从而提高模型的稳定性
2. 非单调性：Mish 的非单调性使得它能够捕捉到更复杂的模式，比 ReLU 等单调激活函数更具表现力
3. 梯度流动：Mish 在负值区域是无界的，这有助于梯度流动，避免梯度消失问题

示例

以下是一个简单的 Python 示例，展示如何计算 Mish 函数：

import numpy as np
import matplotlib.pyplot as plt
 
# 定义 Softplus 函数
def softplus(x):
    return np.log1p(np.exp(x))
 
# 定义 Mish 函数
def mish(x):
    return x * np.tanh(softplus(x))