001.FlashAttention

FlashAttention

Flash Attention 是一种新型的注意力机制算法，由斯坦福大学和纽约州立大学布法罗分校的科研团队共同开发，旨在解决传统 Transformer 模型在处理长序列数据时面临的时间和内存复杂度高的问题。该算法的核心思想是减少 GPU 高带宽内存（HBM）和 GPU 片上 SRAM 之间的内存读写次数，通过分块计算（tiling）和重计算（recomputation）技术，显著降低了对 HBM 的访问频率，从而提升了运行速度并减少了内存使用

Flash Attention 通过 IO 感知的设计理念，优化了内存访问模式，使得 Transformer 模型在长序列处理上更加高效，为构建更长上下文的高质量模型提供了可能

大模型需要的显卡知识

我们需要明确大模型训练与推理的基本需求，大模型通常意味着更高的计算需求和数据存储需求。因此，在选择 GPU 时，我们需要关注其计算能力、显存大小以及与其他硬件设备的兼容性

计算墙，指的是单卡算力和模型总算力之间的巨大差异。A100 的单卡算力只有 312 TFLOPS，而 GPT-3 则需要 314 ZFLOPs 的总算力，两者相差了 9 个数量级

显存墙，指的是单卡无法完整存储一个大模型的参数。GPT-3 的 1750 亿参数本身就需要 700 GB 的显存空间（每个参数按照 4 个字节计算），而 NVIDIA A100 GPU 只有 80 GB 显存

通信墙，主要是分布式训练下集群各计算单元需要频繁参数同步，通信性能将影响整体计算速度。如果通信墙如果处理得不好，很可能导致集群规模越大，训练效率反而会降低

当前显卡的计算能力是大于通信能力的，使得通信成为瓶颈，transformer 的 self-attention，会有大量的 IO，即：将数据从 HBM 读取到 SRAM 中再计算

为此，FlashAttention 的设计理念是通过增加计算量的方式减少 I/O，来平衡当前显卡计算能力强于通信能力的特点

Self-Attention

为了看懂 FlashAttention 的核心算法，让我们从原始的 Self-Attention 开始。参考《From Online Softmax to FlashAttention》

Self-Attention 的计算，去掉 batch 和缩放因子，可以概括为：

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

其中，$Q,K,V,O$ 都是 2 维矩阵，形状是 (L, D)，L 是序列长度，D 是每个头的维度，softmax 函数作用在后面的维度上

标准的计算 self-attention 的计算流程有三步：

$$\begin{array}{rl}X& =Q{K}^T\\ A& =softmax(X)\\ O& =AV\end{array}\text{\hspace{1em}(1)(2)(3)}$$

合并起来：

$$O=softmax(Q{K}^T)V\text{\hspace{1em}(4)}$$

FlashAttention 不需要在全局内存（HBM）上实现 $X$ 和 $A$ 矩阵，而是将公式 $(4)$ 中的整个计算融合到单个 CUDA 内核（cuda-kernel/tensor-kernel）中，这样就不需要大量的 I/O

这要求我们设计一种算法来仔细管理片上内存（on-chip memory，如流算法），因为 NVIDIA GPU 的共享内存（SRAM）很小。对于矩阵乘法等经典算法，使用平铺（tiling）来确保片上内存不超过硬件限制。这种平铺方法是有效的原因是：加法是关联的，允许将整个矩阵乘法分解为许多平铺矩阵乘法的总和

然而，Self-Attention 包含一个不直接关联的 softmax 运算符，因此很难简单地平铺 Self-Attention。有没有办法让 softmax 具有关联性？

Gut-feeling：我们的目标是计算 $O$，一般来说，我们需要获取所有的 $Q,K,V$，然后分三步计算；也可以先获取一小块 $Q,K,V$，一次计算得到部分的 $O$，再想办法将部分的 $O$ 合成全部的 $O$

难点：矩阵是可加的，但是 softmax 是不可加的

解决方案：等比数列

Safe Softmax

对于 softmax，公式如下：

$$softmax(\left\{x_1,...,x_N\right\})={\left\{\frac{e^{x_i}}{{\sum }_{j=1}^N{e}^{x_j}}\right\}}_{i=1}^N\text{\hspace{1em}(5)}$$

$x_i$ 可能会非常大，那 $e_i^x$ 会溢出：float16 最大 65536，那 $x_i$ 大于 12 时，$e^x$ 就超过有效数字了。所以事实上的公式是 safe-softmax：

$$\frac{e^{x_i}}{{\sum }_{j=1}^N{e}^{x_j}}=\frac{e^{x_i-m}}{{\sum }_{j=1}^N{e}^{x_j-m}}\text{\hspace{1em}(6)}$$

其中：

$$m=ma{x}_{j=1}^N(x_j)$$

基于此，我们可以总结下 safe-softmax 的计算步骤，称之为 3 步算法：

• $\{m_i\}$：前 $i$ 个输入 $\{x_j\}$ 中的最大值（$j$ 从 1 到 $i$），初始值 $m_0=-\infty$
• $\{d_i\}$：${\sum }_{j=1}^i{e}^{x_j-m_N}$ 的累加和，初始值 $d_0=0$，$d_N$ 是 safe-softmax 的分母
• $\{a_i\}$：最终的 softmax 值

这就是传统的 self-attention 算法，需要我们从 1 到 N 迭代 3 次。$x_i$ 是由 $QK$ 计算出来的 pre-softmax，这意味着我们需要读取 $Q,K$ 三次，有很大的 I/O 开销

Online Softmax

如果我们在一个循环中融合方程 $(7)(8)(9)$，我们可以将全局内存访问时间从 3 减少到 1。不幸的是，我们不能在同一个循环中融合 $(7)(8)$，因为 $(8)$ 取决于 $m_N$，而 $m_N$ 只有在第一个循环完成之后才能确定

为了移除对 $N$ 的依赖，我们可以创建另一个序列作为原始序列的替代。即找到一个等比数列（递归形式），去除 $N$ 的依赖

$$\begin{array}{rl}{d}_i^{\prime }& =\sum _{j=1}^i{e}^{x_j-m_i}\\ & =\left(\sum _{j=1}^{i-1}{e}^{x_j-m_i}\right)+e^{x_i-m_i}\\ & =\left(\sum _{j=1}^{i-1}{e}^{x_j-m_{i-1}}\right)e^{m_{i-1}-m_i}+e^{x_i-m_i}\\ & =d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}+e^{x_i-m_i}\end{array}\text{\hspace{1em}(10)}$$

这个递归形式只依赖于 $m_i$ 和 $m_i-1$，我们可以在同一个循环中同时计算 $m_j$ 和 $d_j^{\prime }$

这是 Online Softmax 论文中提出的算法。但是，它仍然需要两次传递才能完成 softmax 计算，我们能否将传递次数减少到 1 次以最小化全局 I/O？

FlashAttention

不幸的是，对于 softmax 来说，答案是不行，但在 Self-Attention 中，我们的最终目标不是注意力得分矩阵 $A$，而是等于 $AV$ 的 $O$ 矩阵。我们能找到 $O$ 的一次递归形式吗？将 Self-Attention 计算的第 $k$ 行（所有行的计算都是独立的，为了简单起见，我们只解释一行的计算）公式化为递归算法：

• $Q[k,:]$：矩阵 $Q$ 的第 $k$ 行向量
• $K^T[:,i]$：矩阵 $K^T$ 的第 $i$ 列向量
• $O[k,:]$：输出矩阵 $O$ 的第 $k$ 行
• $V[i,:]$：矩阵 $V$ 的第 $i$ 行
• $\{o_i\}$：${\sum }_{j=1}^i{a}_{j}V[j,:]$，存储部分聚合结果 $A[k,:i]\times V[:i,:]$ 的行向量

我们将公式 $(12)$ 中的 $a_i$ 替换为公式 $(11)$ 中的定义：

$$o_i=\sum _{j=1}^i(\frac{e^{x_j-m_N}}{d_N^{\prime }}V[j,:])\text{\hspace{1em}(13)}$$

这仍然取决于 $m_N$ 和 $d_N$，这两个值在前一个循环完成之前无法确定。但我们可以再次使用 Online softmax 节中的替代技巧，即创建替代序列 $o^{\prime }$：

$$o_i^{\prime }=(\sum _{j=1}^i\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:])$$

我们可以找到 $o_i$ 和 $o_i-1$ 之间的递归关系：

$$\begin{array}{rl}{\mathbf{o}}_i^{\prime }& =\sum _{j=1}^i\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i^{\prime }}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_i-1}}{d_{i-1}^{\prime }}\frac{e^{x_j-m_i}}{e^{x_j-m_{i-1}}}\frac{d_{i-1}^{\prime }}{d_i^{\prime }}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & =\left(\sum _{j=1}^{i-1}\frac{e^{x_j-m_i-1}}{d_{i-1}^{\prime }}V[j,:]\right)\frac{d_{i-1}^{\prime }}{d_i^{\prime }}{e}^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\\ & ={\mathbf{o}}_{i-1}^{\prime }\frac{d_{i-1}^{\prime }{e}^{m_{i-1}-m_i}}{d_i^{\prime }}+\frac{e^{x_i-m_i}}{d_i^{\prime }}V[i,:]\end{array}\text{\hspace{1em}(14)}$$

我们可以将 Self-Attention 中的所有计算融合到一个 loop 中：

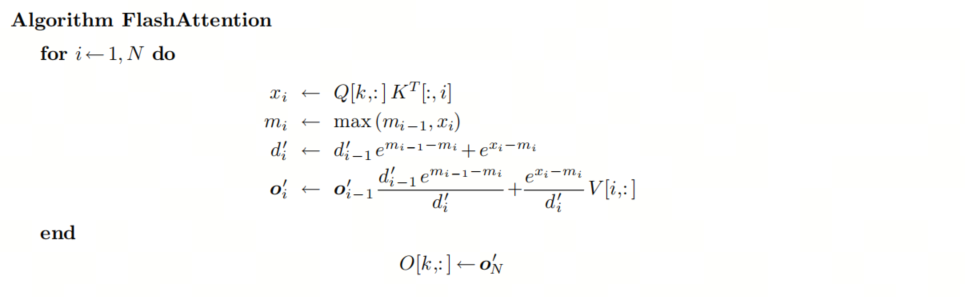
此时，所有的数据都非常小并且可以加载到 GPU 的 SRAM 里面，由于该算法中的所有操作都是关联的，因此它与平铺兼容。如果我们逐个平铺地计算状态，则该算法可以表示如下：

1. 瓦片（Tile）
   • 将大型矩阵分割为 $b\times b$ 的小块
   • 目的：适配 GPU 显存，实现增量计算
2. ​​块大小 $b$​
   • 核心优化参数
   • 典型值：128/256（根据 GPU 架构调整）
3. ​​局部最大值 $m_i^{(local)}$
   • 每个瓦片独立计算的最大值
   • 作用：避免全局 softmax 的数值溢出

算法核心思想是通过分块计算局部最大值和分母，实现：

1. 显存占用从 $O(N^2)$ 降至 $O(N)$
2. 避免大矩阵指数运算的数值不稳定

总结

FlashAttention 最核心的部分是构造出一个递归（等比数列），让部分结果可以累计到全局，这样就不用一下子加载所有值并分步计算了

这个等比数列的构造，大概就是高考最后一道大题的水平