多元函数定义
设 D 为一个非空的 n 元有序数组的集合, 为某一确定的对应规则,也称为函数关系
,如果对于每一个有序数组,通过对应规则 都有唯一确定的实数 与之对应,则称对应规则 为定义在 D 上的 n 元函数。记为:
变量 称为自变量,y 称为因变量
- 当 时,为一元函数,记为
- 当 时,为二元函数,记为 ,如图所示:
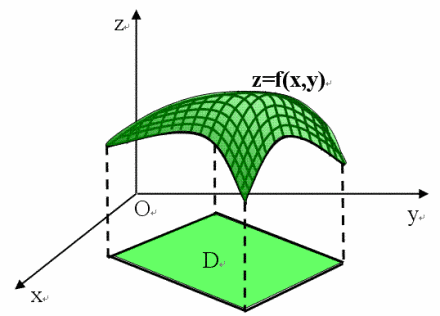
- 二元及以上的函数统称为多元函数
偏导数
偏导数,可以看作是导数的推广,对于多元函数来说,把其它的自变量固定不动,看成是常量,对其中的某一个变量求导数的话,那就是偏导数了,只对一个变量求导数!
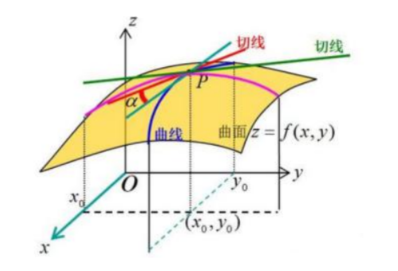
几何意义上面来说就是在某个方向上对原函数来切一下,再去求导,就是偏导数。举例说明:
对变量 求偏导数,其中 是常量:
对变量 求偏导数,则 是常量:
高阶偏导数
有高阶导数,同样也有高阶偏导数,它的情况比高阶导数要复杂一些,因为它的求导变量有多个,比如:
它对 求高阶偏导数的话,就是先对 求偏导,再对 求偏导,其实跟一元函数的高阶导数是一样的,依次对每个变量反复求导即可,我们还是以上面的公式为例:
二元函数的二阶偏导数有四个:
有个重要的结论,就是高阶导数和求导次序无关:
梯度
机器学习中的梯度下降法和牛顿法很多地方都会用到梯度这个概念
梯度可以看成一元函数的导数,对于多元函数来说就是偏导数而已
对于多元函数如果它的自变量有 N 个:。它的梯度是个向量,是由对 变量求偏导数构成的这样一个向量,称之为梯度。梯度我们用倒三角这个符号来表示,对 求梯度得到上面所示的向量
雅可比矩阵
雅克比矩阵定义
这个可能很多同学学高等数学的时候没有学过,但是这个也比较好理解,就是由一阶偏导数构成的矩阵,发明它的目的主要是为了简化求导公式,对多元的复合函数求导,如果我们用雅可比矩阵来计算的话,它会写起来非常简洁,这在我们的人工神经网络反向推导的过程中往往会看到的
,其中 是 n 维向量,表示有 n 个未知数,即 n 个自变量; 是 k 维的向量,表示函数对应关系计算返回 k 个因变量
,其中每个 和每个 都是相关的,也就是每个 是单独从 映射过来的函数
函数 的雅可比矩阵就是每个 分别对每个 求偏导,然后构成的矩阵叫做雅可比矩阵:
第一行就是 对 求偏导;第二行是 对 求偏导;第 k 行是 对 求偏导。如果 是 n 维向量, 是 k 个值的因变量,那么雅可比矩阵就是 的矩阵
雅克比矩阵示例
自变量 根据函数 映射为因变量 ,那么 是 的函数, 也是 的函数,那么函数 的雅可比矩阵如下:
Hessian 矩阵
Hessian 矩阵定义
Hessian 矩阵是对于一个多元函数来说的,它就相当于一元函数的二阶偏导数
有一个关于 的 n 元函数 ,自变量为 ,那么 Hessian 矩阵为:
Hessian 矩阵是一个 的矩阵,里面的元素是二阶偏导数构成的。第一个元素是对 求二阶偏导数,第二个元素是对 求偏导数,因为多元函数高阶偏导数和顺序无关,所以 Hessian 矩阵是对称矩阵
Hessian 矩阵示例
首先求函数 的一阶偏导数:
然后求解 Hessian 矩阵:
Hessian 矩阵和函数的凹凸性是有密切关系的,如果 Hessian 矩阵正定,可以说函数 是凸函数,如果是负定,它就是凹函数
矩阵正定是如何判定的呢?
极值判别法则
极值判定条件
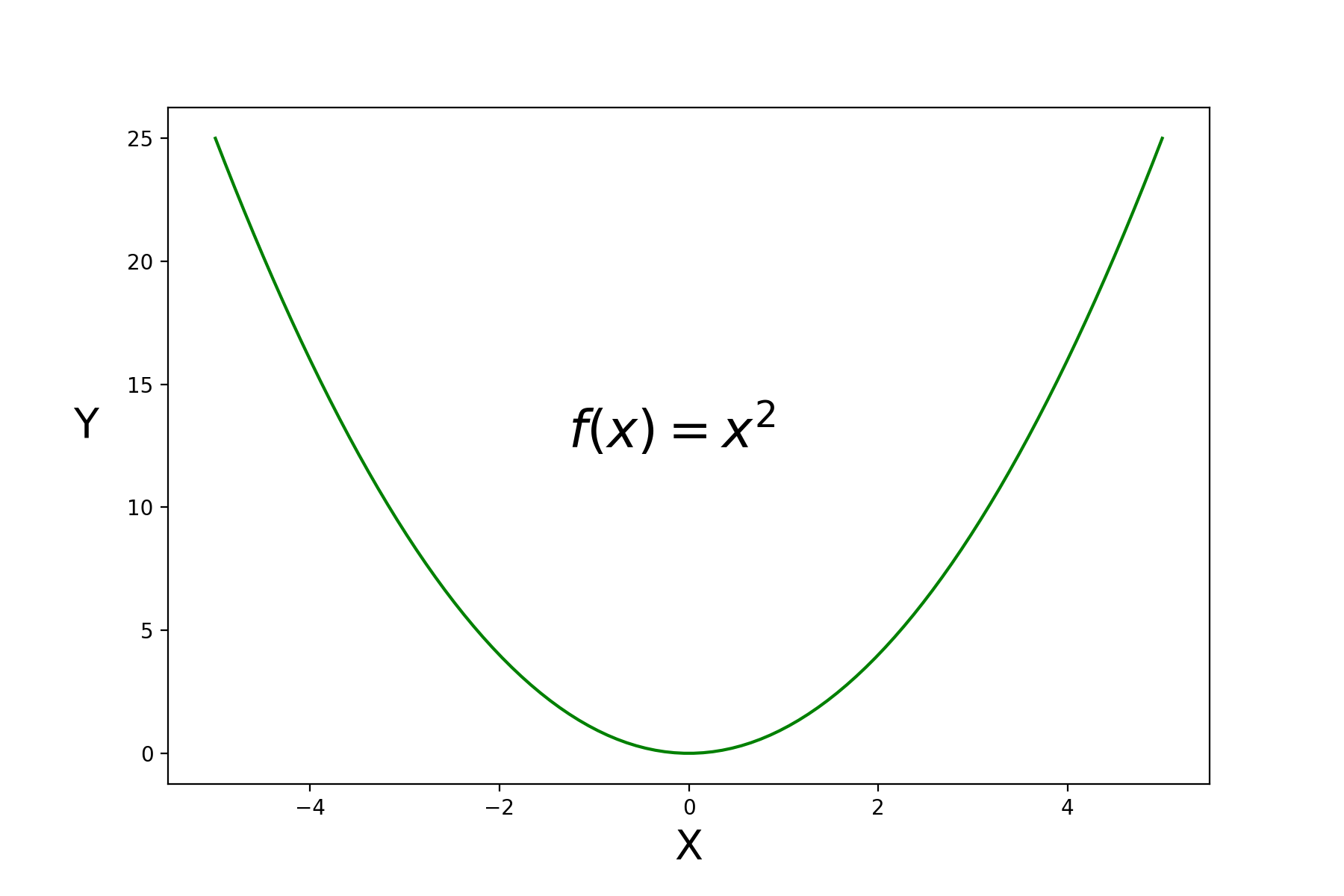
对于一元函数, 的一阶导数等于 0 处有极值,当 的二阶导数大于 0 时是极小值,当 的二阶导数小于 0 时是极大值,可以参考 的平方这个函数,其二阶导数是 ,那么该函数是凸函数
多元函数的极值判别法则,首先 的一阶导数等于 0,这点是驻点,那它就可能是极值点,它是极大值还是极小值或者不是极值怎么判定的?
看 Hessian 矩阵,满足在 的一阶导数等于 0 处(驻点处)下:
- 如果 Hessian 矩阵是正定的话,函数在该点有极小值
- 如果 Hessian 矩阵是负定的话,函数在该点有极大值
- 如果 Hessian 矩阵不定,函数在该点不是极值
实对称矩阵正定负定判定
实对称矩阵 A 正定负定判定条件:
- 对于任意向量 ,都有 ,那么 A 就是正定矩阵
- 对于任意向量 ,都有 ,那么 A 就是负定矩阵
实对称矩阵 A 负定,代码演示:
import numpy as np
A = np.array([[-2,-3,-1],
[-3,-6,-4],
[-1,-4,-5]])
# v 任意给值(除了 0 向量),结果总是负数
v = np.random.randint(-50,50,size=3)
print('给定向量任意向量 v:', v)
print('求解矩阵 A 正定判定条件结果是:', v.T.dot(A).dot(v))
'''
给定向量任意向量 v: [3 5 6]
求解矩阵 A 正定判定条件结果是: -714
'''实对称矩阵 A 正定,代码演示:
import numpy as np
A = np.array([[5,1,-4],
[1,3,-2],
[-4,-2,7]])
# v 任意给值(除了 0 向量),结果总是正数
v = np.random.randint(-50,50,size=3)
print('给定向量任意向量 v:', v)
print('求解矩阵 A 正定判定条件结果是:', v.T.dot(A).dot(v))
'''
给定向量任意向量 v: [ 2 -3 -5]
求解矩阵 A 正定判定条件结果是: 128
'''但是这样不太容易判断,我们还可以根据特征值正负去判断矩阵正定与否:
- 矩阵 A 的特征值全部大于 0,那么矩阵 A 为正定矩阵
- 矩阵 A 的特征值全部小于 0,那么矩阵 A 为负定矩阵
实对称矩阵 A 负定,特征值代码演示:
import numpy as np
A = np.array([[-2,-3,-1],
[-3,-6,-4],
[-1,-4,-5]])
w,v = np.linalg.eig(A)
print('矩阵 A 的特征值特征向量是:')
display(w, v)
'''
矩阵 A 的特征值特征向量是:
array([-10.54287655, -0.03922866, -2.41789479])
array([[ 0.32798528, 0.73697623, -0.59100905],
[ 0.73697623, -0.59100905, -0.32798528],
[ 0.59100905, 0.32798528, 0.73697623]])
'''实对称矩阵 A 正定,特征值代码演示:
import numpy as np
A = np.array([[5,1,-4],
[1,3,-2],
[-4,-2,7]])
w,v = np.linalg.eig(A)
print('矩阵 A 的特征值特征向量是:')
display(w, v)
'''
矩阵 A 的特征值特征向量是:
array([10.74515039, 1.63251546, 2.62233415])
array([[-0.58123713, -0.60851363, -0.54025416],
[-0.27299496, -0.4796241 , 0.83392714],
[ 0.76657495, -0.63219608, -0.11265418]])
'''二次型
二次型定义
二次型就是纯二次项构成的一个函数
因为二次函数的二次部分最重要,为了方便研究,我们把含有 n 个变量的二次齐次函数:
称为二次型
二次型表示
可以通过矩阵来进行表示:
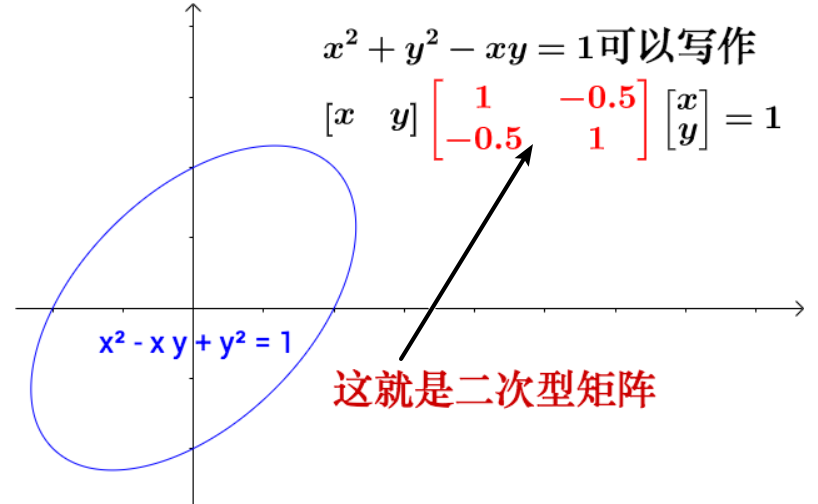
二次型通俗表现形式:
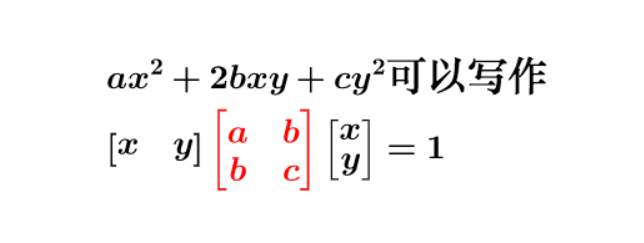
二次型矩阵表示:
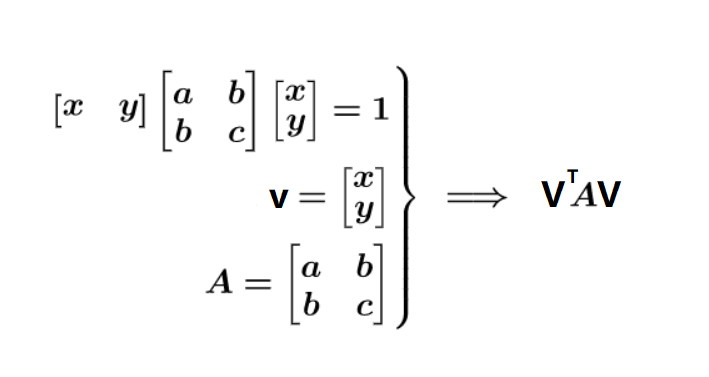
n 个变量的二次齐次函数矩阵表示:
三种写法完全等价
二次型应用
在机器学习中,我们可以根据数据分布进行模型选择:
- 如果数据分布是一次型的,那就可以选择 Logistic Regression、SVM 等分界面为一次型的模型
- 如果数据分布是二次型的,可以选择 naive bayes
- 如果数据分布既不是一次型也不是二次型,那可以选择基于决策树的模型,例如 GBDT、随机森林等,或 DNN(深度神经网络),这些模型都高度非线性,表达能力极强,理论上可以拟合任意曲线
Hessian 矩阵与二次型
将 Hessian 矩阵 A 转换为二次型:
,其中 表示非零任意向量
- ,则 为正定二次型,A 为正定矩阵
- ,则 为半正定二次型,A 为半正定矩阵
- ,则 为负定二次型,A 为负定矩阵
- ,则 为半负定二次型,A 为半负定矩阵
- 以上皆不是,就叫做不定
正定效果图:有唯一极小值
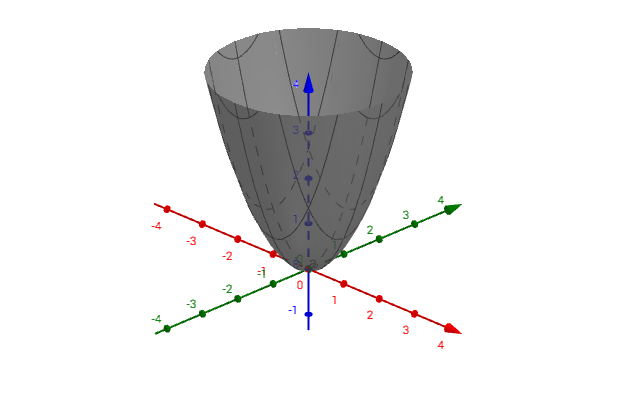
半正定效果图:有一组极小值
不定效果图:没有极小值或极大值,随着数据扩张,极小值或极大值也扩张