030.二维前缀和、二维差分、离散化技巧

前置知识：一维差分、前缀和、最优性剪枝

二维前缀和 §

原理 §

目的是预处理出一个结构，以后每次查询二维数组任何范围上的累加和都是 $O(1)$ 的操作

其实就是 一维前缀和 的二维化，目的、原理、实现思路都是一致的

根据原始二维数组，生成二维前缀和数组 sum：

• sum[i][j]：左上角 $(0,0)$ 到右下角 $(i,j)$ 这个范围的累加和
• sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + sum[i][j]
  • 即：左 + 上 - 左上 + 自己

查询左上角 $(a,b)$ 到右下角 $(c,d)$ 这个范围的累加和：

• sum[c][d] - sum[c][b-1] - sum[a-1][d] + sum[a-1][b-1]
  • 即：自己 - 左 - 上 + 左上

实际过程中往往补第 0 行、第 0 列来减少很多条件判断。当然也可以不补，根据题目变化和个人习惯决定

题目1.二维前缀和模版 §

测试链接 §

304.二维区域和检索 - 矩阵不可变

答案 §

type NumMatrix [][]int
 
func Constructor(matrix [][]int) NumMatrix {
	n := len(matrix)
	m := len(matrix[0])
	ans := make([][]int, n+1)
	for i := range ans {
		ans[i] = make([]int, m+1)
	}
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			ans[i+1][j+1] = matrix[i][j]
		}
	}
	for i := 1; i <= n; i++ {
		for j := 1; j <= m; j++ {
			ans[i][j] += ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1]
		}
	}
	return NumMatrix(ans)
}
 
func (this NumMatrix) SumRegion(a int, b int, c int, d int) int {
	c++
	d++
	return this[c][d] - this[c][b] - this[a][d] + this[a][b]
}

题目2.边框为 1 的最大正方形 §

题目描述 §

给你一个由若干 0 和 1 组成的二维网格 grid，请你找出边界全部由 1 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 0。

测试链接 §

1139.最大的以 1 为边界的正方形

复杂度与思路 §

首先要遍历矩阵中的所有正方形，其时间复杂度为 $O(n\ast m\ast min(n,m))$，其中 $n\ast m$ 为正方形左上顶点、$min(n,m)$ 为正方形边长

如果暴力判断正方形 4 条边长是否都是 1 的话，时间复杂度为 $O(4\ast min(n,m))$，即暴力方法总时间复杂度为 $O(n\ast m\ast min(n,m)\ast 4\ast min(n,m))$

可以用二维前缀和优化判断正方形 4 条边长是否都是 1 为 $O(1)$，具体做法是求 $正方形面积-除去边长的小正方形面积$ 是否等于 $正方形的边长$

所以，二维前缀和方法的时间复杂度是 $O(n\ast m\ast min(n,m))$，空间复杂度是 $O(1)$（复用原矩阵构建前缀和），复杂度指标上绝对是最优解，打败比例不高完全是常数时间的问题（有些方法可以通过增加空间来优化时间复杂度的常数时间）

答案 §

var (
	g [][]int
	n int
	m int
)
 
func largest1BorderedSquare(grid [][]int) int {
	n = len(grid)
	m = len(grid[0])
	g = grid
	build()
 
	// 特判：整个矩阵没有 1 或者只有一个 1，没必要遍历了
	allSum := sum(0, 0, n-1, m-1)
	if allSum == 0 || allSum == 1 {
		return allSum
	}
 
	// 找到的最大合法正方形的边长
	ans := 1
	for a := 0; a < n; a++ {
		for b := 0; b < m; b++ {
			// 当前尝试的边长
			// 最优性剪枝：从更大的边长开始找
			k := ans + 1
			for {
				c := a + k - 1
				d := b + k - 1
				if c >= n || d >= m {
					break
				}
				if sum(a, b, c, d)-sum(a+1, b+1, c-1, d-1) == (k-1)<<2 {
					ans = k
					k = ans + 1
				} else {
					k++
				}
			}
		}
	}
	// 面积
	return ans * ans
}
 
// 为了节省空间复杂度，用原矩阵构建前缀和
// 不能补 0 行 0 列
func build() {
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			g[i][j] += get(i-1, j) + get(i, j-1) - get(i-1, j-1)
		}
	}
}
 
func sum(a, b, c, d int) int {
	if c < a || d < b {
		return 0
	}
	return get(c, d) - get(a-1, d) - get(c, b-1) + get(a-1, b-1)
}
 
// 就需要对下标进行边界判断了
func get(i, j int) int {
	if i < 0 || j < 0 {
		return 0
	}
	return g[i][j]
}

二维差分 §

原理 §

就是 一维差分 的二维化，目的、原理、实现思路都是一致的

• set 方法：如下图所示
• build 方法：进行 二维前缀和

真实数据可以用一圈 0 包裹起来，可以减少很多边界讨论

差分方法对原始数组的要求

题目1.二维差分模版 §

测试链接 §

• ACM 模式 - 牛客：【模板】二维差分
• ACM 模式 - 洛谷：P3397 地毯

答案 §

package main
 
import (
	"bufio"
	"os"
	"strconv"
)
 
const (
	MAXN = 1005
	MAXM = 1005
)
 
var (
	matrix = [MAXN][MAXM]int{}
	n      int
	m      int
)
 
func main() {
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		in.Scan()
		m, _ = strconv.Atoi(in.Text())
		in.Scan()
		q, _ := strconv.Atoi(in.Text())
		// startup
		for i := 1; i <= n; i++ {
			for j := 1; j <= m; j++ {
				in.Scan()
				v, _ := strconv.Atoi(in.Text())
				set(i, j, i, j, v)
			}
		}
		for ; q > 0; q-- {
			in.Scan()
			a, _ := strconv.Atoi(in.Text())
			in.Scan()
			b, _ := strconv.Atoi(in.Text())
			in.Scan()
			c, _ := strconv.Atoi(in.Text())
			in.Scan()
			d, _ := strconv.Atoi(in.Text())
			in.Scan()
			v, _ := strconv.Atoi(in.Text())
			set(a, b, c, d, v)
		}
		build()
		for i := 1; i <= n; i++ {
			out.WriteString(strconv.Itoa(matrix[i][1]))
			for j := 2; j <= m; j++ {
				out.WriteByte(' ')
				out.WriteString(strconv.Itoa(matrix[i][j]))
			}
			out.WriteByte('\n')
		}
		clear()
	}
	out.Flush()
}
 
func set(a, b, c, d, v int) {
	matrix[a][b] += v
	matrix[c+1][b] -= v
	matrix[a][d+1] -= v
	matrix[c+1][d+1] += v
}
 
func build() {
	// 二维前缀和
	for i := 1; i <= n; i++ {
		for j := 1; j <= m; j++ {
			matrix[i][j] += matrix[i-1][j] + matrix[i][j-1] - matrix[i-1][j-1]
		}
	}
}
 
func clear() {
	for i := 1; i <= n+1; i++ {
		for j := 1; j <= m+1; j++ {
			matrix[i][j] = 0
		}
	}
}

题目2.用邮票贴满网格图 §

二维前缀和 + 二维差分

题目描述 §

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

测试链接 §

2132.用邮票贴满网格图

答案 §

func possibleToStamp(grid [][]int, stampHeight int, stampWidth int) bool {
	n := len(grid)
	m := len(grid[0])
 
	// 前缀和矩阵：用于查询 grid 中某个范围是否可以贴邮票（累加和 =0）
	sum := make([][]int, n+1)
	sum[0] = make([]int, m+1)
	for i := 0; i < n; i++ {
		sum[i+1] = make([]int, m+1)
		for j := 0; j < m; j++ {
			sum[i+1][j+1] = grid[i][j]
		}
	}
	build(sum)
 
	// 差分矩阵
	// 当贴邮票的时候，不在原始矩阵里贴，在差分矩阵里贴
	// 原始矩阵就用来判断能不能贴邮票，不进行修改
	// 每贴一张邮票都在差分矩阵里修改
	diff := make([][]int, n+2)
	for i := range diff {
		diff[i] = make([]int, m+2)
	}
	a, b, c, d := 1, 1, 1, 1
	for {
		b = 1
		c = a + stampHeight - 1
		if c > n {
			break
		}
		for {
			d = b + stampWidth - 1
			if d > m {
				break
			}
			// 贪心：能贴就贴上
			if sumRegion(sum, a, b, c, d) == 0 {
				set(diff, a, b, c, d, 1)
			}
			b++
		}
		a++
	}
	build(diff)
 
	// 检查所有格子
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			// 是洞且没贴邮票
			if grid[i][j] == 0 && diff[i+1][j+1] == 0 {
				return false
			}
		}
	}
	return true
}
 
// 构建二维前缀和
func build(matrix [][]int) {
	n := len(matrix)
	m := len(matrix[0])
	for i := 1; i < n; i++ {
		for j := 1; j < m; j++ {
			matrix[i][j] += matrix[i-1][j] + matrix[i][j-1] - matrix[i-1][j-1]
		}
	}
}
 
// 二维前缀和求范围累加和
func sumRegion(matrix [][]int, a, b, c, d int) int {
	return matrix[c][d] - matrix[c][b-1] - matrix[a-1][d] + matrix[a-1][b-1]
}
 
// 二维差分添加操作
func set(matrix [][]int, a, b, c, d, v int) {
	matrix[a][b] += v
	matrix[c+1][d+1] += v
	matrix[a][d+1] -= v
	matrix[c+1][b] -= v
}

复杂度 §

• 时间复杂度：$O(n\ast m)$
• 空间复杂度：$O(n\ast m)$

题目3.最强祝福力场 §

题目描述 §

forceField[i] = [x,y,side] 表示第 i 片力场将覆盖以坐标 (x,y) 为中心，边长为 side 的正方形区域。

任意一点的 力场强度 等于覆盖该点的力场数量，请求出在这片地带中 力场强度 最强处的 力场强度。

注意：力场范围的边缘同样被力场覆盖。

示例 1：

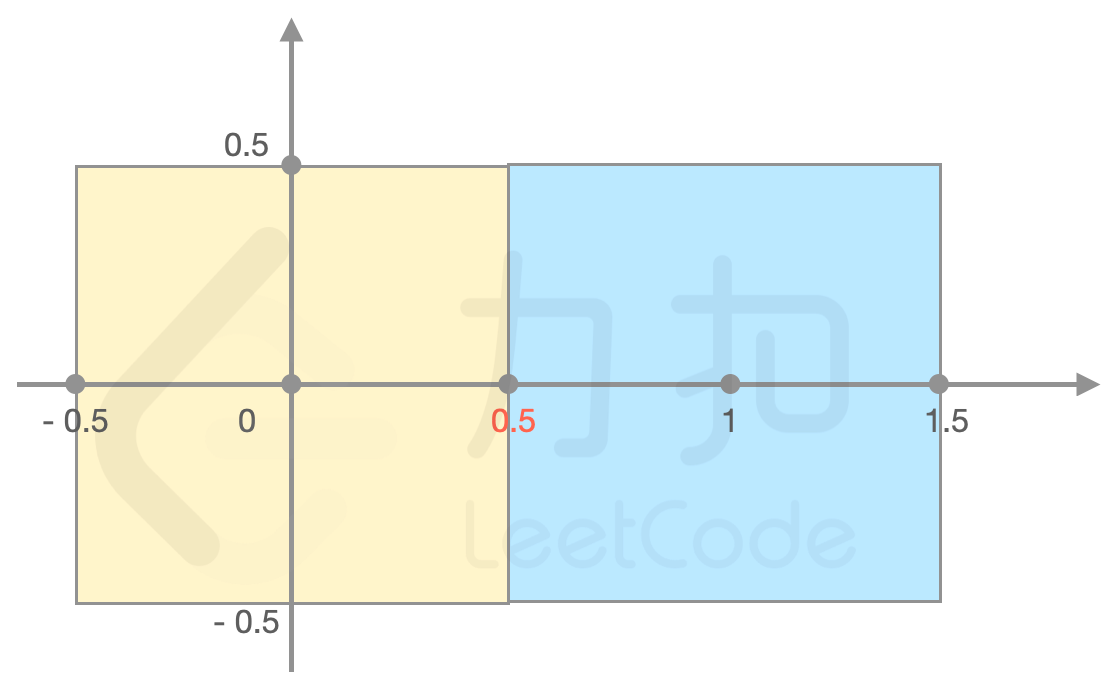
输入：forceField = [[0,0,1],[1,0,1]]

输出：2

解释：如下图所示，(0.5, 0) 处力场强度最强为 2， (0.5，-0.5) 处力场强度同样是 2

示例 2：

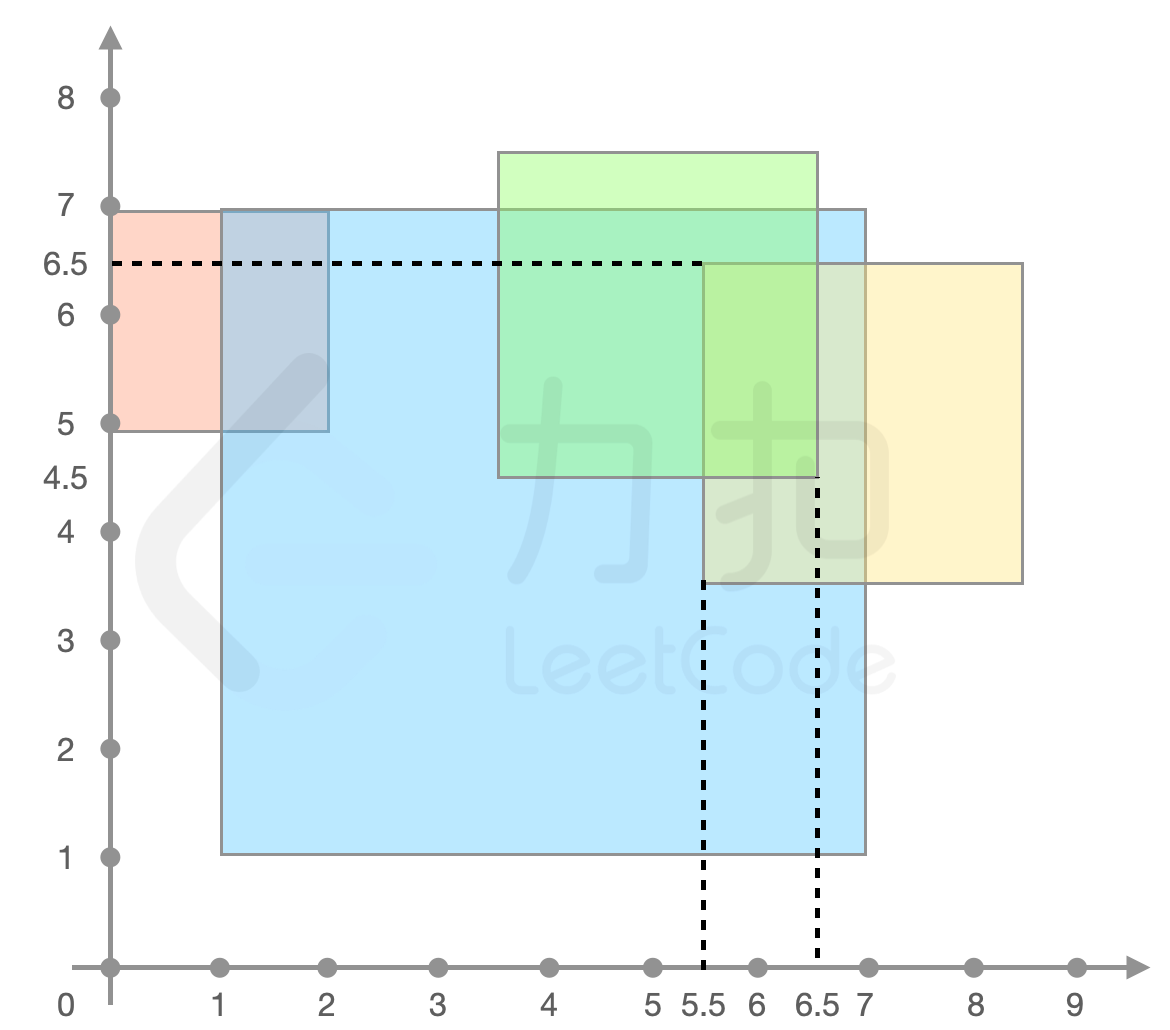
输入：forceField = [[4,4,6],[7,5,3],[1,6,2],[5,6,3]]

输出：3

解释：如下图所示，forceField[0]、forceField[1]、forceField[3] 重叠的区域力场强度最大，返回 3

提示：

• 1 <= forceField.length <= 100
• forceField[i].length == 3
• 0 <= forceField[i][0], forceField[i][1] <= 10^9
• 1 <= forceField[i][2] <= 10^9

测试链接 §

LCP 74.最强祝福力场

离散化技巧 §

如上图所示，坐标可能落到 0.5 的单位上，int 无法表示，需要将其等比扩大，使其不出现小数（等比扩大不会使力场辐射范围的相对位置发生变化）：

// 若力场原点在 (x, y) 处，辐射直径径为 d
// 则力场辐射的范围为：
left   := x - d/2
right  := x + d/2
top    := y - d/2
bottom := y + d/2
// 其中 d 可能为 1，则 d/2 就出现了 0.5 小数
// 等比扩大：将其扩大一倍，就不会出现小数了
left   := (x << 1) - d // (x - d/2) * 2
right  := (x << 1) + d
top    := (y << 1) - d
bottom := (y << 1) + d

看数据量发现力场原点的坐标范围到 $10^9$，开辟二维差分数组的话需要 $10^{18}$ 的空间，这是不现实的，而 forceField 的长度范围是 100，一个 forceField 需要左右（上下）两个坐标，数据量是 $200\ast 200$ 的空间，所以要用离散化技巧缩小二维差分数组的空间，具体做法是：

答案 §

func fieldOfGreatestBlessing(forceField [][]int) int {
	n := len(forceField)
	// 每个矩形两个坐标
	xs := make([]int, n<<1)
	ys := make([]int, n<<1)
	for i, s := 0, 0; i < n; i, s = i+1, s+2 {
		x := forceField[i][0]
		y := forceField[i][1]
		d := forceField[i][2]
		xs[s] = (x << 1) - d
		xs[s+1] = (x << 1) + d
		ys[s] = (y << 1) - d
		ys[s+1] = (y << 1) + d
	}
	xSize := sortAndUnique(xs)
	ySize := sortAndUnique(ys)
	// 二维差分矩阵
	diff := make([][]int, xSize+2)
	for i := range diff {
		diff[i] = make([]int, ySize+2)
	}
	for i := 0; i < n; i++ {
		x := forceField[i][0]
		y := forceField[i][1]
		d := forceField[i][2]
		// diff 最前面多一位，所以要 +1
		a := getIdx(xs, (x<<1)-d, xSize) + 1
		b := getIdx(ys, (y<<1)-d, ySize) + 1
		c := getIdx(xs, (x<<1)+d, xSize) + 1
		d := getIdx(ys, (y<<1)+d, ySize) + 1
		set(diff, a, b, c, d)
	}
	ans := 0
	for i := 1; i < xSize+1; i++ {
		for j := 1; j < ySize+1; j++ {
			diff[i][j] += diff[i-1][j] + diff[i][j-1] - diff[i-1][j-1]
			ans = max(ans, diff[i][j])
		}
	}
	return ans
}
 
// 排序数组并去重，返回去重后的数组长度
func sortAndUnique(arr []int) int {
	sort.Ints(arr)
	n := len(arr)
	size := 1
	for i := 1; i < n; i++ {
		if arr[i] != arr[size-1] {
			arr[size] = arr[i]
			size++
		}
	}
	return size
}
 
// arr 有序，有效长度是 size，0~size-1 范围上无重复值
// 已知 v 一定在 nums[0:size]，返回 v 的索引
func getIdx(arr []int, v, size int) int {
	l, r, m := 0, size-1, 0
	for l <= r {
		m = l + (r-l)>>1
		if arr[m] > v {
			r = m - 1
		} else if arr[m] < v {
			l = m + 1
		} else {
			return m
		}
	}
	panic("v 不在数组中")
}
 
// 二维差分添加操作
func set(diff [][]int, a, b, c, d int) {
	diff[a][b] += 1
	diff[c+1][d+1] += 1
	diff[a][d+1] -= 1
	diff[c+1][b] -= 1
}

复杂度 §

• 时间复杂度：$O(n^2)$，$n$ 是力场个数
• 空间复杂度：$O(n^2)$

备注 §

支持实时单点修改 + 实时查询的结构是二维树状数组，会在【扩展】课程里讲述