044.宽度优先遍历及其扩展

前置知识：会使用 队列、双端队列、优先级队列（堆）、二叉树上的宽度优先遍历、经典递归过程解析、图

本节课讲述：

• 单源、多源宽度优先遍历基本过程
• 01bfs，宽度优先遍历与双端队列结合
• 宽度优先遍历与优先级队列结合
• 宽度优先遍历与深度优先遍历结合，去生成路径

宽度优先遍历基本内容 §

1. bfs 的特点是逐层扩散，从源头点到目标点扩散了几层，最短路就是多少
2. bfs 可以使用的特征是任意两个节点之间的相互距离相同（无向图）
   • 从 A 扩到 B 和 从 B 扩到 A 都是层数 +1
   • 如果是有向图：A -> B 权重 1，B -> A 权重 2，则一般宽度优先遍历是不行的
   • 要使用 Dijkstra 算法 来解
3. bfs 开始时，可以是单个源头、也可以是多个源头
4. bfs 频繁使用队列，形式可以是单点弹出或者整层弹出
5. bfs 进行时，进入队列的节点需要标记状态，防止同一个节点重复进出队列
   • visited：标识一个节点是否已经处理过了，处理过的节点再遇到就直接跳过
6. bfs 进行时，可能会包含 剪枝 策略的设计
7. bfs 是一个理解难度很低的算法，难点在于节点如何找到路、路的展开和剪枝设计

题目1.地图分析 §

题目描述 §

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 不是 0 就是 1

测试链接 §

1162.地图分析

思路 §

题目相当于求：从陆地出发（所有陆地同时出发），能达到的最远海洋

小技巧：优雅完成向上下左右移动

move := []int{-1, 0, 1, 0, -1}
 
for i := 0; i < 4; i++ {
	// (x, y): (x + move[i], y + move[i+1])
	// i 来到 0 位置: (x-1, y)，向上
	// i 来到 1 位置: (x, y+1)，向右
	// i 来到 2 位置: (x+1, y)，向下
	// i 来到 3 位置: (x, y-1)，向左
}

答案 §

const (
	MAXN = 101
)
 
var (
	n          int
	queue      = [MAXN * MAXN][2]int{}
	head, tail = 0, 0
	visited    = [MAXN][MAXN]bool{}
	move       = [5]int{-1, 0, 1, 0, -1}
)
 
func maxDistance(grid [][]int) int {
	head, tail = 0, 0
	n = len(grid)
	seas := 0
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			if grid[i][j] == 1 {
				visited[i][j] = true
				// 多个源头
				queue[tail][0] = i
				queue[tail][1] = j
				tail++
			} else {
				visited[i][j] = false
				seas++
			}
		}
	}
 
	if seas == 0 || seas == n*n {
		return -1
	}
 
	level := 0
	size := 0
	x, y := 0, 0
	nextX, nextY := 0, 0
	for head < tail {
		level++
		size = tail - head
		// 整层弹出
		for i := 0; i < size; i++ {
			x = queue[head+i][0]
			y = queue[head+i][1]
			for j := 0; j < 4; j++ {
				nextX = x + move[j]
				nextY = y + move[j+1]
				if nextX >= 0 && nextX < n && nextY >= 0 && nextY < n && !visited[nextX][nextY] {
					visited[nextX][nextY] = true
					queue[tail][0] = nextX
					queue[tail][1] = nextY
					tail++
				}
			}
		}
		head += size
	}
 
	return level - 1
}

复杂度 §

• 时间复杂度：$O(n\ast m)$，矩阵的大小
  • 遍历矩阵每个位置上下左右扩，不管怎么扩，每个位置只处理一次（进出队列一次）
• 空间复杂度：$O(n\ast m)$，队列

题目2.贴纸拼词 §

题目描述 §

我们有 n 种不同的贴纸。每个贴纸上都有一个小写的英文单词。

您想要拼写出给定的字符串 target ，方法是从收集的贴纸中切割单个字母并重新排列它们。如果你愿意，你可以多次使用每个贴纸，每个贴纸的数量是无限的。

返回你需要拼出 target 的最小贴纸数量。如果任务不可能，则返回 -1 。

注意：在所有的测试用例中，所有的单词都是从 1000 个最常见的美国英语单词中随机选择的，并且 target 被选择为两个随机单词的连接。

提示:

• n == stickers.length
• 1 <= n <= 50
• 1 <= stickers[i].length <= 10
• 1 <= target.length <= 15
• stickers[i] 和 target 由小写英文单词组成

测试链接 §

691.贴纸拼词

思路 §

还可以用动态规划来解

答案 §

const (
	MAXN = 401
)
 
var (
	// 每个字母，存在于哪些字符串
	graph = [26][]string{}
	// 哪些字符串访问过
	visited     = map[string]struct{}{}
	emptyStruct = struct{}{}
	queue       = [MAXN]string{}
	head, tail  = 0, 0
)
 
func minStickers(stickers []string, target string) int {
	build()
	for _, str := range stickers {
		byteArr := []byte(str)
		sort.Slice(byteArr, func(i, j int) bool {
			return byteArr[i] < byteArr[j]
		})
		for i, v := range byteArr {
			if i > 0 && v == byteArr[i-1] {
				continue
			}
			graph[v-'a'] = append(graph[v-'a'], string(byteArr))
		}
	}
	targetByteArr := []byte(target)
	sort.Slice(targetByteArr, func(i, j int) bool {
		return targetByteArr[i] < targetByteArr[j]
	})
	queue[tail] = string(targetByteArr)
	visited[queue[tail]] = emptyStruct
	tail++
	level := 1
	for head < tail {
		size := tail - head // 处理一层
		for i := 0; i < size; i++ {
			cur := queue[head+i]
			// 所有字符都要解决（每个字符迟早都要解决），不妨先解决第一个字符
			for _, str := range graph[cur[0]-'a'] {
				rest := handle(str, cur)
				if rest == "" {
					return level
				} else if _, has := visited[rest]; !has {
					visited[rest] = emptyStruct
					queue[tail] = rest
					tail++
				}
			}
		}
		level++
		head += size
	}
	return -1
}
 
// 用 str 消除 target 中的字符，两个 字符串都是排序好的
// 返回消除后剩余的字符
func handle(str, target string) string {
	var builder strings.Builder
	s, t := 0, 0
	strLen, tarLen := len(str), len(target)
	for s < strLen && t < tarLen {
		if target[t] < str[s] {
			builder.WriteByte(target[t])
			t++
		} else if target[t] > str[s] {
			s++
		} else {
			s++
			t++
		}
	}
	if t < tarLen {
		builder.WriteString(target[t:])
	}
	return builder.String()
}
 
func build() {
	for i := 0; i < 26; i++ {
		clear(graph[i])
	}
	clear(visited)
	head, tail = 0, 0
}

01bfs §

适用于图中所有边的权重只有 0 和 1 两种值，求源点到目标点的最短距离

时间复杂度为 $O(节点数量+边的数量)$

为什么不能用传统 bfs？ §

传统 bfs 下面的那条路会先走到 B，B 节点标记为已访问过的节点，上面那条路就不会走到了。或者修改逻辑可以走到，也会导致后来的值修改之前的值，逻辑很难写

除非将边先按权重进行排序后再使用传统 bfs，但这样的话时间复杂度太高了

思路 §

1. distance[i] 表示从源点到 i 点的最短距离，初始时所有点的 distance 设置为无穷大
2. 源点进入双端队列，distance[源点] = 0（自己到自己的距离为 0）
3. 双端队列，头部弹出 x
   • 如果 x 是目标点，返回 distance[x] 表示源点到目标点的最短距离
   • 否则考察从 x 出发的每一条边，假设某边去 y 点，边权为 w
     • 如果 distance[y] > distance[x] + w，处理该边；否则忽略该边
     • 处理时，更新 distance[y] = distance[x] + w。如果 w==0，y 从头部进入双端队列；如果 w==1，y 从尾部进入双端队列
     • 考察完 x 出发的所有边之后，重复步骤 3
4. 双端队列为空停止

正确性证明 §

正确性证明以及为什么不需要 visited 来标记节点

双端队列中任意两个节点，原点和它们的距离差不会超过 1

从头部出队列的元素 distance[x] 就是它到原点的距离

• w==1：从尾部进入双端队列
• w==0：从头部进入双端队列

权重为 0，从头部进就修正了它的距离，使其变得更小。即使双端队列后面还有一个相同的元素弹出时，它的 distance[x] 已经被之前弹出的相同元素修正对了。一个节点最多进双端队列两次，这也正是不需要 visited 来标记节点的原因

题目1.到达角落需要移除障碍物的最小数目 §

题目描述 §

给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n 。每个单元格都是两个值之一：

• 0 表示一个 空 单元格，
• 1 表示一个可以移除的 障碍物 。

你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。

现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ，返回需要移除的障碍物的 最小 数目。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10^5
• 2 <= m * n <= 10^5
• grid[i][j] 为 0 或 1
• grid[0][0] == grid[m - 1][n - 1] == 0

测试链接 §

2290.到达角落需要移除障碍物的最小数目

思路 §

01bfs 模板

答案 §

const (
	MAX_INT = math.MaxInt
)
 
var (
	move = [5]int{-1, 0, 1, 0, -1}
)
 
func minimumObstacles(grid [][]int) int {
	n := len(grid)
	m := len(grid[0])
	distance := make([][]int, n)
	for i := range distance {
		distance[i] = make([]int, m)
		for j := 0; j < m; j++ {
			distance[i][j] = MAX_INT // 默认无穷大，表示无联通
		}
	}
	distance[0][0] = 0
	deque := NewDeque[[2]int](m * n)
	deque.Unshift([2]int{0, 0})
	for !deque.IsEmpty() {
		record, _ := deque.Shift()
		x := record[0]
		y := record[1]
		if x == n-1 && y == m-1 {
			return distance[x][y]
		}
		for i := 0; i < 4; i++ {
			nx := x + move[i]
			ny := y + move[i+1]
			if nx < 0 || nx == n || ny < 0 || ny == m {
				continue
			}
			if distance[x][y]+grid[nx][ny] >= distance[nx][ny] {
				continue
			}
			distance[nx][ny] = distance[x][y] + grid[nx][ny]
			if grid[nx][ny] == 0 {
				deque.Unshift([2]int{nx, ny})
			} else {
				deque.Push([2]int{nx, ny})
			}
		}
	}
	return -1
}

其中 Deque 是 数组实现 的代码

题目1.使网格图至少有一条有效路径的最小代价 §

题目描述 §

给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：

• 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]
• 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]
• 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]
• 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

示例 1：

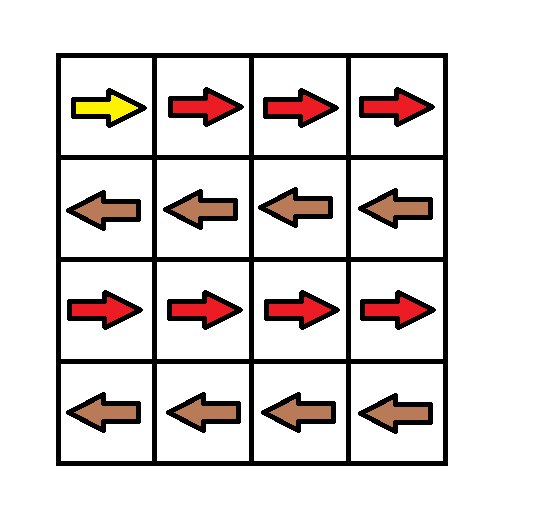
输入：grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]

输出：3

解释：你将从点 (0, 0) 出发。到达 (3, 3) 的路径为： (0, 0) —> (0, 1) —> (0, 2) —> (0, 3) 花费代价 cost = 1 使方向向下 —> (1, 3) —> (1, 2) —> (1, 1) —> (1, 0) 花费代价 cost = 1 使方向向下 —> (2, 0) —> (2, 1) —> (2, 2) —> (2, 3) 花费代价 cost = 1 使方向向下 —> (3, 3)。总花费为 cost = 3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100

测试链接 §

1368.使网格图至少有一条有效路径的最小代价

思路 §

将箭头方向和要走的方向一样看成 0，不一样需要 1 代价修改看成 1，就转换成 01bfs 了

答案 §

const (
	MAX_INT = math.MaxInt
)
 
var (
	move = [5][2]int{
		{},
		{0, 1},  // 1 向右
		{0, -1}, // 2 向左
		{1, 0},  // 3 向下
		{-1, 0}, // 4 向上
	}
)
 
func minCost(grid [][]int) int {
	n := len(grid)
	m := len(grid[0])
	distance := make([][]int, n)
	for i := range distance {
		distance[i] = make([]int, m)
		for j := 0; j < m; j++ {
			distance[i][j] = MAX_INT
		}
	}
	distance[0][0] = 0
	deque := NewDeque[[2]int](n * m)
	deque.Unshift([2]int{0, 0})
	for !deque.IsEmpty() {
		record, _ := deque.Shift()
		x := record[0]
		y := record[1]
		if x == n-1 && y == m-1 {
			return distance[x][y]
		}
		for i := 1; i <= 4; i++ {
			nx := x + move[i][0]
			ny := y + move[i][1]
			if nx < 0 || nx == n || ny < 0 || ny == m {
				continue
			}
			cost := 1
			if grid[x][y] == i {
				cost = 0
			}
			if distance[nx][ny] <= distance[x][y]+cost {
				continue
			}
			distance[nx][ny] = distance[x][y] + cost
			if cost == 0 {
				deque.Unshift([2]int{nx, ny})
			} else {
				deque.Push([2]int{nx, ny})
			}
		}
	}
	return -1
}

其中 Deque 是 数组实现 的代码

宽度优先遍历与优先级队列结合 §

宽度优先遍历与优先级队列结合，更进一步的内容会在讲 Dijkstra 算法 时说明

宽度优先遍历与深度优先遍历结合，去生成路径

• bfs 建图
• dfs 利用图生成路径

题目1.二维接雨水 §

题目描述 §

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1：

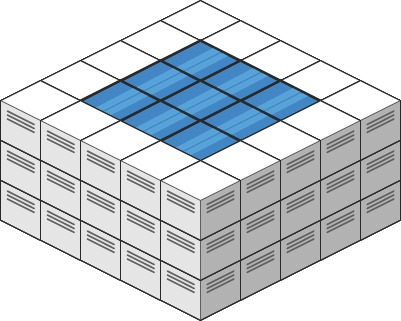
输入：heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]

输出：10

提示：

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 10^4

测试链接 §

407.接雨水 II

思路 §

结合优先级队列进行 bfs，贪心

答案 §

var (
	move = []int{-1, 0, 1, 0, -1}
)
 
func trapRainWater(heightMap [][]int) int {
	n := len(heightMap)
	m := len(heightMap[0])
	minHeap := make(MinHeap, 0, (n+m)<<1)
	visited := make([][]bool, n)
	for i := range visited {
		visited[i] = make([]bool, m)
	}
 
	// 将边框加入堆
	for i := 0; i < n; i++ {
		minHeap = append(minHeap, [3]int{i, 0, heightMap[i][0]}, [3]int{i, m - 1, heightMap[i][m-1]})
		visited[i][0] = true
		visited[i][m-1] = true
	}
	for j := 0; j < m; j++ {
		minHeap = append(minHeap, [3]int{0, j, heightMap[0][j]}, [3]int{n - 1, j, heightMap[n-1][j]})
		visited[0][j] = true
		visited[n-1][j] = true
	}
	heap.Init(&minHeap)
 
	ans := 0
	for minHeap.Len() > 0 {
		// 弹出最低的柱子壁垒高度，进行结算
		record := heap.Pop(&minHeap).([3]int)
		x := record[0]
		y := record[1]
		v := record[2]
		// 四周可不可能更低？不可能！因为一开始就把四个边界都加进去了，不可能有更低的高度了
		// 所以当前结算就是正确的
		ans += v - heightMap[x][y] // 最低的壁垒高度 - 当前柱子高度 = 当前柱子能接的雨水
		for i := 0; i < 4; i++ {
			nx := x + move[i]
			ny := y + move[i+1]
			if nx < 0 || nx == n || ny < 0 || ny == m || visited[nx][ny] {
				continue
			}
			// 下一个位置的壁垒高度 = max(下一个位置柱子高度，当前壁垒高度)
			heap.Push(&minHeap, [3]int{nx, ny, max(heightMap[nx][ny], v)})
			visited[nx][ny] = true
		}
	}
	return ans
}
 
// [行, 列, 水线]
type MinHeap [][3]int
 
func (h MinHeap) Len() int {
	return len(h)
}
 
func (h MinHeap) Less(i, j int) bool {
	return h[i][2] < h[j][2]
}
 
func (h MinHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}
 
func (h *MinHeap) Push(v any) {
	*h = append(*h, v.([3]int))
}
 
func (h *MinHeap) Pop() any {
	n := len(*h)
	res := (*h)[n-1]
	*h = (*h)[:n-1]
	return res
}

题目2.单词接龙 II §

题目描述 §

按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列，并满足：

• 每对相邻的单词之间仅有单个字母不同。
• 转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。
• sk == endWord

给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, ..., sk] 的形式返回。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]

输出：[["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]]

解释：存在 2 种最短的转换序列：

"hit" -> "hot" -> "dot" -> "dog" -> "cog"

"hit" -> "hot" -> "lot" -> "log" -> "cog"

提示：

• 1 <= beginWord.length <= 5
• endWord.length == beginWord.length
• 1 <= wordList.length <= 500
• wordList[i].length == beginWord.length
• beginWord、endWord 和 wordList[i] 由小写英文字母组成
• beginWord != endWord
• wordList 中的所有单词 互不相同

测试链接 §

126.单词接龙 II

思路 §

bfs 建图，图从 end 向 begin 指，这样就不会收集到不可达的路径

收集答案用 dfs（回溯）

最后收集答案再反转一下，或者使用链表头插收集

答案 §

var (
	// 方便查询：array -> set
	dict      map[string]struct{}
	ans       = [][]string{}
	curLevel  = map[string]struct{}{}
	nextLevel = map[string]struct{}{}
	// 反向图
	graph = map[string][]string{}
	// 记录路径，当生成一条有效路的时候，拷贝进 ans
	path        = []string{}
	emptyStruct = struct{}{}
)
 
func build(wordList []string) {
	// 方便查询：array -> set
	dict = make(map[string]struct{}, len(wordList))
	for _, word := range wordList {
		dict[word] = emptyStruct
	}
	// clear(ans) // 坑：clear 不会将 ans 置空，而是将 ans 的元素都置空了
	ans = ans[:0]
	clear(curLevel)
	clear(nextLevel)
	clear(graph)
	clear(path)
}
 
func findLadders(beginWord string, endWord string, wordList []string) [][]string {
	build(wordList)
	if _, has := dict[endWord]; !has {
		// 永远变不到
		return ans
	}
 
	if bfs(beginWord, endWord) {
		fmt.Println(graph)
		dfs(endWord, beginWord)
	}
 
	reverse()
 
	return ans
}
 
// 从 begin 到 end 一层层 bfs，建图
// 返回是否能到 end
func bfs(begin, end string) bool {
	find := false
	curLevel[begin] = emptyStruct
	for len(curLevel) > 0 {
		for k := range curLevel {
			delete(dict, k) // 相当于 visited 的作用
		}
		for k := range curLevel {
			word := []byte(k)
			wordLen := len(word)
			for i := 0; i < wordLen; i++ {
				old := word[i]
				var char byte = 'a'
				for ; char <= 'z'; char++ {
					if char == old {
						continue
					}
					word[i] = char
					wordStr := string(word)
					if _, has := dict[wordStr]; has {
						if wordStr == end {
							find = true
						}
						_, has := graph[wordStr]
						if !has {
							graph[wordStr] = []string{}
						}
						graph[wordStr] = append(graph[wordStr], k) // k 变一个单词变成 wordStr
						nextLevel[wordStr] = emptyStruct
					}
					word[i] = old // 回溯
				}
			}
		}
		if find {
			return true
		} else {
			curLevel, nextLevel = nextLevel, curLevel
			clear(nextLevel)
		}
	}
 
	return false
}
 
// 已经将答案都反向收集到 graph 了，用 dfs 整理答案
func dfs(word, aim string) {
	path = append(path, word)
	if word == aim {
		curAns := make([]string, len(path))
		copy(curAns, path)
		ans = append(ans, curAns)
	} else if strArr, has := graph[word]; has {
		for _, next := range strArr {
			dfs(next, aim)
		}
	}
	path = path[:len(path)-1]
}
 
// 收集到的答案是反的，反转一下
func reverse() {
	for _, cur := range ans {
		l, r := 0, len(cur)-1
		for l < r {
			cur[l], cur[r] = cur[r], cur[l]
			l++
			r--
		}
	}
}

坑 §

注意 go 中的 clear() 方法只会清空最后一个维度的数据，并不是清空第一个维度的数据

package main
 
import "fmt"
 
func main() {
	arr := [][]int{}
	arr = append(arr, []int{1, 2})
	arr = append(arr, []int{3, 4})
	clear(arr)
	fmt.Println(len(arr)) // 2，并不是 0
	fmt.Println(arr) // [[] []]，并不是 []
}