056.分组背包、完全背包

前置知识：讲解067、讲解068 二维动态规划及其空间压缩技巧、01背包、有依赖的背包

分组背包、完全背包 §

• 分组背包：与 01 背包的区别仅在于多个物品分组，每组只能取 1 件
  • 每一组的物品都可能性展开就可以了
  • 时间复杂度不会升阶：$O(物品数量\ast 背包容量)$
  • 空间复杂度：$O(背包容量)$
  • 题目1 ~ 题目2
• 完全背包：与 01 背包的区别仅在于每种商品可以选取无限次
  • 时间复杂度：$O(物品数量\ast 背包容量)$
  • 空间复杂度：$O(背包容量)$
  • 题目3 ~ 题目6

题目1.分组背包模版 §

题目描述 §

给定一个正数 m 表示背包的容量，有 n 个货物可供挑选

每个货物有自己的体积（容量消耗）、价值（获得收益）、组号（分组）

同一个组的物品只能挑选 1 件，所有挑选物品的体积总和不能超过背包容量

怎么挑选货物能达到价值最大，返回最大的价值

测试链接 §

P1757 通天之分组背包

思路 §

dp[i][j]：前 i（或者说第 1 ~ 第 i 个，共 i 个）组中，每组最多只能选 1 件商品，容量不超过 j 的情况下，能获得的最大价值

注意：dp 表中的 i 代表组，而不是商品

状态转移：

1. 不要 i 组商品：从前 i-1 组中选，即：dp[i-1][j]
2. 要 i 组商品：要哪一件？全试！
   • 商品 a：dp[i-1][j-a的体积] + a的价值
   • 商品 b：dp[i-1][j-b的体积] + b的价值
   • …

以上情况取最大值即是 dp[i][j]

位置依赖：每个格子依赖上（dp[i-1][j]）和左上某一个格子（dp[i-1][j-costs[i]]）

所以从上往下推，将第一行进行初始化即可

初始化：dp[0][*] 代表没有物品可选，最大价值应该都是 0

空间压缩：i 层只依赖 i-1 层左侧位置，滚动数组，从上往下、从右往左递推

和 01 背包 基本一致

答案 §

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"sort"
	"strconv"
)
 
const (
	MAXN = 1001
	MAXM = 1001
)
 
var (
	m   int              // 背包容量
	n   int              // 物品数量
	arr = [MAXN][3]int{} // [体积, 价值, 组号]
	dp  = [MAXM]int{}
)
 
func main() {
	// s := `45 3
	// 10 10 1
	// 10 5 1
	// 50 400 2`
	// in := bufio.NewScanner(strings.NewReader(s))
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		m, _ = strconv.Atoi(in.Text())
		in.Scan()
		n, _ = strconv.Atoi(in.Text())
		for i := 1; i <= n; i++ {
			in.Scan()
			arr[i][0], _ = strconv.Atoi(in.Text())
			in.Scan()
			arr[i][1], _ = strconv.Atoi(in.Text())
			in.Scan()
			arr[i][2], _ = strconv.Atoi(in.Text())
		}
		// 同一组放到一起
		sort.Slice(arr[1:n+1], func(i, j int) bool {
			return arr[i][2] < arr[j][2]
		})
		fmt.Fprintln(out, compute())
	}
	out.Flush()
}
 
// 严格位置依赖的动态规划：略
 
// 空间压缩
func compute() int {
	for i := 0; i < m+1; i++ {
		dp[i] = 0
	}
	for start, end := 1, 2; start <= n; {
		for end <= n && arr[start][2] == arr[end][2] {
			end++
		}
		// arr[start:end] 是同一组的物品
		for j := m; j >= 0; j-- {
			for k := start; k < end; k++ {
				if j-arr[k][0] >= 0 {
					dp[j] = max(dp[j], dp[j-arr[k][0]]+arr[k][1])
				}
			}
		}
		start = end
		end++
	}
	return dp[m]
}

题目2.从栈中取出 K 个硬币的最大面值和 §

题目描述 §

一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的 顶部 取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在 恰好 进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少 。

示例 1：

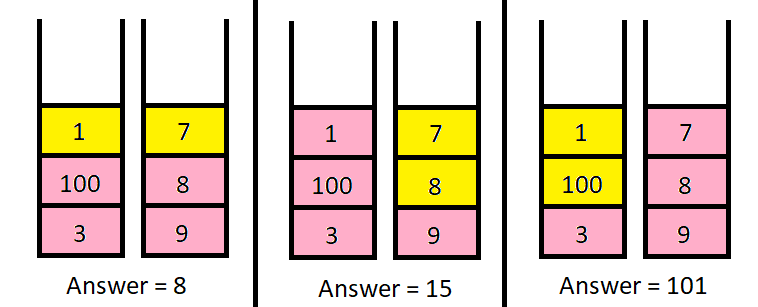
输入：piles = [[1,100,3],[7,8,9]], k = 2

输出：101

解释：上图展示了几种选择 k 个硬币的不同方法。我们可以得到的最大面值为 101

提示：

• n == piles.length
• 1 <= n <= 1000
• 1 <= piles[i][j] <= 10^5
• 1 <= k <= sum(piles[i].length) <= 2000

测试链接 §

2218.从栈中取出 K 个硬币的最大面值和

思路 §

每个栈只能从最上边开始拿，并不是“任取其一”，怎么用分组背包？

分组：

• 每个栈取最上面 1 个，价值是最上面硬币的价值，消耗是 1
• 每个栈取最上面 2 个，价值是最上面 2 的硬币的价值和，消耗是 2
• …

这样就转化为 分组背包 问题了

答案 §

func maxValueOfCoins(piles [][]int, k int) int {
	n := len(piles)
	dp := make([]int, k+1)
	for i := 0; i < n; i++ {
		// 每一组：最多所有硬币都用上，或者用前 k 个
		t := min(len(piles[i]), k)
		// piles[i][j]：最上面 j+1 个硬币累加和
		for j := 1; j < t; j++ {
			piles[i][j] += piles[i][j-1]
		}
		for j := k; j >= 0; j-- {
			// j：防止 j-(l+1) 下标越界
			// t：该组最多有 t 个物品
			for l := 0; l < min(j, t); l++ {
				dp[j] = max(dp[j], dp[j-(l+1)]+piles[i][l])
			}
		}
	}
	return dp[k]
}

题目3.完全背包模版 §

题目描述 §

给定一个正数 t，表示背包的容量

有 m 种货物，每种货物可以选择任意个

每种货物都有体积 costs[i] 和价值 values[i]

返回在不超过总容量的情况下，怎么挑选货物能达到价值最大

返回最大的价值

测试链接 §

P1616 疯狂的采药

思路 §

dp[i][j]：只对前 i 个（或者说第 1 ~ 第 i 个，共 i 个）物品进行选择，当背包容量为 j 时，可以装的最大价值

状态转移：

1. 不选第 i 件物品：就是在前 i-1 件物品中选，即 dp[i-1][j]
2. 选第 i 件物品：因为第 i 件商品可以选择无数次，所有继续在前 i 件物品中选 + 选第 i 件物品，dp[i][j-costs[i]] + values[i]

位置依赖：每个格子依赖上（dp[i-1][j]）和左某一个格子（dp[i][j-costs[i]]）

所以从上往下、从左往右推，将第一行和第一列进行初始化即可

初始化：

• dp[0][*] 代表没有物品可选，最大价值应该都是 0
• dp[*][0] 代表没有背包容量，最大价值应该都是 0

其实第一列不初始化也行，因为 dp[*][0] 必然来自上格子（dp[i-1][0] == 0），因为 dp[i][0-costs[i]]，0-costs[i] 必然为负，不取

空间压缩：i 层只依赖 i-1 层左侧位置，滚动数组，从上往下、从左往右递推

这里与 01 背包 不同的是：

• 01 背包空间压缩是从右往左推，因为格子依赖左上，从右往左防止依赖的格子被改值
• 完全背包空间压缩是从左往右推，因为格子依赖左，从左往右确保被依赖的格子已经正确

答案 §

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXT = 1e7 + 1
	MAXM = 1e4 + 1
)
 
var (
	t    int           // 背包容量
	m    int           // 物品数量
	cost = [MAXM]int{} // 体积
	val  = [MAXM]int{} // 价值
	dp   = [MAXT]int{}
)
 
func main() {
	// s := `70 3
	// 71 100
	// 69 1
	// 1 2`
	// in := bufio.NewScanner(strings.NewReader(s))
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		t, _ = strconv.Atoi(in.Text())
		in.Scan()
		m, _ = strconv.Atoi(in.Text())
		for i := 1; i <= m; i++ {
			in.Scan()
			cost[i], _ = strconv.Atoi(in.Text())
			in.Scan()
			val[i], _ = strconv.Atoi(in.Text())
		}
		fmt.Fprintln(out, compute2())
	}
	out.Flush()
}
 
// 严格位置依赖的动态规划
func compute1() int {
	dp := make([][]int, m+1)
	for i := range dp {
		dp[i] = make([]int, t+1)
	}
	for i := 1; i <= m; i++ {
		for j := 1; j <= t; j++ {
			dp[i][j] = dp[i-1][j]
			if j-cost[i] >= 0 {
				dp[i][j] = max(dp[i][j], dp[i][j-cost[i]]+val[i])
			}
		}
	}
	return dp[m][t]
}
 
// 空间压缩
func compute2() int {
	for j := 0; j <= t; j++ {
 
	}
	for i := 1; i <= m; i++ {
		for j := cost[i]; j <= t; j++ {
			dp[j] = max(dp[j], dp[j-cost[i]]+val[i])
		}
	}
	return dp[t]
}

题目4.正则表达式匹配 §

题目描述 §

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

• '.'：匹配任意单个字符
• '*'：匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"

输出：false

解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"

输出：true

解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"

输出：true

解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

• 1 <= s.length <= 20
• 1 <= p.length <= 20
• s 只包含从 a-z 的小写字母。
• p 只包含从 a-z 的小写字母，以及字符 . 和 *。
• 保证每次出现字符 * 时，前面都匹配到有效的字符

测试链接 §

10.正则表达式匹配

暴力递归 §

var (
	S    string
	P    string
	sLen int
	pLen int
)
 
func isMatch(s string, p string) bool {
	S = s
	P = p
	sLen = len(s)
	pLen = len(p)
	return f(0, 0)
}
 
// s[i:] 能不能被 p[j:] 完全匹配出来
// 会保证 p[j] 这个字符，一定不是 '*'
func f(i, j int) bool {
	if i == sLen {
		// s 到了结尾
		if j == pLen {
			// p 也到了结尾，说明能匹配上
			return true
		} else {
			// p 还剩下一些后缀
			// 如果 p[j+1] 是 *，那么 p[j:j+2] 可以消掉，然后看看 p[j+2:] 是不是都能消掉
			return j+1 < pLen && P[j+1] == '*' && f(i, j+2)
		}
	} else if j == pLen {
		// s 有后缀，而 p 没后缀了，一定匹配不上
		return false
	} else {
		// s 和 p 都没到结尾
		if j+1 == pLen || P[j+1] != '*' {
			// 如果 p 是最后一个字符，或者 j 的下一个字符不是 *
			// 则当前字符必须要匹配
			return (S[i] == P[j] || P[j] == '.') && f(i+1, j+1)
		} else {
			// p[j+1] 是 *
			// 即：完全背包
 
			// 选择 1：当前 p[j:j+2] 是 x*，就是不让它搞定 s[i]
			p1 := f(i, j+2)
			// 选择 2：当当前 p[j:j+2] 是 x*，看能不能搞定 s[i]
			p2 := (S[i] == P[j] || P[j] == '.') && f(i+1, j)
			// 两个选择，有一个可以搞定就返回 true，都无法搞定返回 false
			return p1 || p2
		}
	}
}

记忆化搜索 §

• i 的范围是 $[0,sLen]$
• j 的范围是 $[0,pLen]$

var (
	S     string
	P     string
	sLen  int
	pLen  int
	cache [][]*bool
)
 
func isMatch(s string, p string) bool {
	S = s
	P = p
	sLen = len(s)
	pLen = len(p)
	cache = make([][]*bool, sLen+1)
	for i := range cache {
		cache[i] = make([]*bool, pLen+1)
	}
	return f(0, 0)
}
 
// s[i:] 能不能被 p[j:] 完全匹配出来
// 会保证 p[j] 这个字符，一定不是 '*'
func f(i, j int) bool {
	if cache[i][j] != nil {
		return *cache[i][j]
	}
	ans := false
	if i == sLen {
		// s 到了结尾
		if j == pLen {
			// p 也到了结尾，说明能匹配上
			ans = true
		} else {
			// p 还剩下一些后缀
			// 如果 p[j+1] 是 *，那么 p[j:j+2] 可以消掉，然后看看 p[j+2:] 是不是都能消掉
			ans = j+1 < pLen && P[j+1] == '*' && f(i, j+2)
		}
	} else if j == pLen {
		// s 有后缀，而 p 没后缀了，一定匹配不上
		ans = false
	} else {
		// s 和 p 都没到结尾
		if j+1 == pLen || P[j+1] != '*' {
			// 如果 p 是最后一个字符，或者 j 的下一个字符不是 *
			// 则当前字符必须要匹配
			ans = (S[i] == P[j] || P[j] == '.') && f(i+1, j+1)
		} else {
			// p[j+1] 是 *
			// 即：完全背包
 
			// 选择 1：当前 p[j:j+2] 是 x*，就是不让它搞定 s[i]
			p1 := f(i, j+2)
			// 选择 2：当当前 p[j:j+2] 是 x*，看能不能搞定 s[i]
			p2 := (S[i] == P[j] || P[j] == '.') && f(i+1, j)
			// 两个选择，有一个可以搞定就返回 true，都无法搞定返回 false
			ans = p1 || p2
		}
	}
 
	cache[i][j] = &ans
	return ans
}

位置依赖 §

func isMatch(s string, p string) bool {
	sLen := len(s)
	pLen := len(p)
	dp := make([][]bool, sLen+1)
	for i := range dp {
		dp[i] = make([]bool, pLen+1)
	}
 
	// 初始化
	dp[sLen][pLen] = true
	for j := pLen - 1; j >= 0; j-- {
		dp[sLen][j] = j+1 < pLen && p[j+1] == '*' && dp[sLen][j+2]
	}
 
	for i := sLen - 1; i >= 0; i-- {
		for j := pLen - 1; j >= 0; j-- {
			if j+1 == pLen || p[j+1] != '*' {
				dp[i][j] = (s[i] == p[j] || p[j] == '.') && dp[i+1][j+1]
			} else {
				dp[i][j] = dp[i][j+2] || (s[i] == p[j] || p[j] == '.') && dp[i+1][j]
			}
		}
	}
	return dp[0][0]
}

空间压缩 §

func isMatch(s string, p string) bool {
	sLen := len(s)
	pLen := len(p)
	dp := make([]bool, pLen+1)
 
	// 初始化最后一行
	dp[pLen] = true
	for j := pLen - 1; j >= 0; j-- {
		dp[j] = j+1 < pLen && p[j+1] == '*' && dp[j+2]
	}
 
	bottomRight, backup := false, false
	for i := sLen - 1; i >= 0; i-- {
		// 每遍历到新行：dp[i][pLen-1] 的右下角是 dp[i+1][pLen]
		bottomRight = dp[pLen]
		// 初始化：dp[*][pLen] = false
		dp[pLen] = false
		for j := pLen - 1; j >= 0; j-- {
			// 下一次遍历元素的右下角是当前元素
			backup = dp[j]
			if j+1 == pLen || p[j+1] != '*' {
				dp[j] = (s[i] == p[j] || p[j] == '.') && bottomRight
			} else {
				dp[j] = dp[j+2] || (s[i] == p[j] || p[j] == '.') && dp[j]
			}
			bottomRight = backup
		}
	}
	return dp[0]
}

题目5.通配符匹配 §

和 题目4 高度相似，只是边界条件不同而已，而且更简单

题目描述 §

给你一个输入字符串 (s) 和一个字符模式 (p) ，请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配：

• '?'：可以匹配任何单个字符。
• '*'：可以匹配任意字符序列（包括空字符序列）。

判定匹配成功的充要条件是：字符模式必须能够 完全匹配 输入字符串（而不是部分匹配）。

提示：

• 0 <= s.length, p.length <= 2000
• s 仅由小写英文字母组成
• p 仅由小写英文字母、'?' 或 '*' 组成

测试链接 §

44.通配符匹配

暴力递归 §

var (
	S    string
	P    string
	sLen int
	pLen int
)
 
func isMatch(s string, p string) bool {
	S = s
	P = p
	sLen = len(s)
	pLen = len(p)
	return f(0, 0)
}
 
// s[i:] 能不能被 p[j:] 完全匹配出来
func f(i, j int) bool {
	if i == sLen {
		// s 到了结尾
		if j == pLen {
			// p 也到了结尾，说明能匹配上
			return true
		} else {
			// p 还剩下一些后缀
			// 如果 p[j] 是 *，可以消掉，然后看看 p[j+1:] 是不是都能消掉
			return P[j] == '*' && f(i, j+1)
		}
	} else if j == pLen {
		// s 有后缀，而 p 没后缀了，一定匹配不上
		return false
	} else {
		if P[j] != '*' {
			// 如果 p[j] 不是 *，那么当前的字符必须能匹配：(s[i] == p[j] || p[j] == '?')
			// 同时，后续也必须匹配上：f(i+1, j+1)
			return (S[i] == P[j] || P[j] == '?') && f(i+1, j+1)
		} else {
			// 完全背包
			// 如果 p[j] 是 *
			// 选择 1：虽然当前 p[j] 是 *，但就是不让它搞定 s[i]，即 * 匹配空串：f(i, j+1)
			// 选择 2：反正当前 p[j] 是 *，必然可以搞定 s[i]，那么继续：f(i+1, j)
			// 两种选择有一个能走通，答案就是 true；如果都搞不定，答案就是 false
			return f(i, j+1) || f(i+1, j)
		}
	}
}

记忆化搜索 §

• i 的范围是 $[0,sLen]$
• j 的范围是 $[0,pLen]$

var (
	S     string
	P     string
	sLen  int
	pLen  int
	cache [][]*bool
)
 
func isMatch(s string, p string) bool {
	S = s
	P = p
	sLen = len(s)
	pLen = len(p)
	cache = make([][]*bool, sLen+1)
	for i := range cache {
		cache[i] = make([]*bool, pLen+1)
	}
	return f(0, 0)
}
 
// s[i:] 能不能被 p[j:] 完全匹配出来
func f(i, j int) bool {
	if cache[i][j] != nil {
		return *cache[i][j]
	}
 
	ans := false
	if i == sLen {
		// s 到了结尾
		if j == pLen {
			// p 也到了结尾，说明能匹配上
			ans = true
		} else {
			// p 还剩下一些后缀
			// 如果 p[j] 是 *，可以消掉，然后看看 p[j+1:] 是不是都能消掉
			ans = P[j] == '*' && f(i, j+1)
		}
	} else if j == pLen {
		// s 有后缀，而 p 没后缀了，一定匹配不上
		ans = false
	} else {
		if P[j] != '*' {
			// 如果 p[j] 不是 *，那么当前的字符必须能匹配：(s[i] == p[j] || p[j] == '?')
			// 同时，后续也必须匹配上：f(i+1, j+1)
			ans = (S[i] == P[j] || P[j] == '?') && f(i+1, j+1)
		} else {
			// 完全背包
			// 如果 p[j] 是 *
			// 选择 1：虽然当前 p[j] 是 *，但就是不让它搞定 s[i]，即 * 匹配空串：f(i, j+1)
			// 选择 2：反正当前 p[j] 是 *，必然可以搞定 s[i]，那么继续：f(i+1, j)
			// 两种选择有一个能走通，答案就是 true；如果都搞不定，答案就是 false
			ans = f(i, j+1) || f(i+1, j)
		}
	}
 
	cache[i][j] = &ans
	return ans
}

位置依赖 §

func isMatch(s string, p string) bool {
	sLen := len(s)
	pLen := len(p)
	dp := make([][]bool, sLen+1)
	for i := range dp {
		dp[i] = make([]bool, pLen+1)
	}
 
	// 初始化
	dp[sLen][pLen] = true
	for j := pLen - 1; j >= 0; j-- {
		dp[sLen][j] = p[j] == '*' && dp[sLen][j+1]
	}
 
	for i := sLen - 1; i >= 0; i-- {
		for j := pLen - 1; j >= 0; j-- {
			if p[j] != '*' {
				dp[i][j] = (s[i] == p[j] || p[j] == '?') && dp[i+1][j+1]
			} else {
				dp[i][j] = dp[i][j+1] || dp[i+1][j]
			}
		}
	}
 
	return dp[0][0]
}

空间压缩 §

func isMatch(s string, p string) bool {
	sLen := len(s)
	pLen := len(p)
	dp := make([]bool, pLen+1)
 
	// 初始化最后一行
	dp[pLen] = true
	for j := pLen - 1; j >= 0; j-- {
		dp[j] = p[j] == '*' && dp[j+1]
	}
 
	bottomRight, backup := false, false
	for i := sLen - 1; i >= 0; i-- {
		bottomRight = dp[pLen]
		dp[pLen] = false
		for j := pLen - 1; j >= 0; j-- {
			backup = dp[j]
			if p[j] != '*' {
				dp[j] = (s[i] == p[j] || p[j] == '?') && bottomRight
			} else {
				dp[j] = dp[j+1] || dp[j]
			}
			bottomRight = backup
		}
	}
 
	return dp[0]
}

题目6.购买足量干草的最小花费 §

题目描述 §

有 n 个提供干草的公司，每个公司都有两个信息

• cost[i] 代表购买 1 次产品需要花的钱
• val[i] 代表购买 1 次产品所获得的干草数量

每个公司的产品都可以购买任意次

你一定要至少购买 h 数量的干草，返回最少要花多少钱

数据规模：

• 1 <= n <= 100
• 1 <= h <= 50000
• 1 <= cost[i], val[i] <= 5000

测试链接 §

P2918【USACO08NOV】Buying Hay S

思路 §

尝试 1 §

dp[i][j]：在前 i（第 1 ~ 第 i）个公司里买，买的干草严格为 j 的情况下，最少花多少钱

$dp表大小\approx 干草公司数量\ast 购买干草的数量=100\ast 50000=5\ast 10^6$

尝试 2 §

dp[i][j]：在前 i（第 1 ~ 第 i）个公司里买，花钱不超过 j 的情况下，最多买多少干草

$dp表大小\approx 干草公司数量\ast 要花的钱$

其中要花的钱最差情况是每个干草价值为 1，花费为 5000，等于 $50000/1\ast 5000$

数据量要比尝试 1 大很多，所以要选择尝试 1

这就是后序需要讲的动态规划中根据数据量猜解法的技巧

答案转换 §

答案是要至少购买 h 数量的干草，返回最少要花多少钱；尝试 1 dp 是买的干草严格为 j 的情况下，最少花多少钱

如何转换？

答案一定在 dp[n][h] ~ dp[n][h+maxVal] 之间，所以将 dp 表扩充到 dp[n][h+maxVal] 即可

答案 §

package main
 
import (
	"bufio"
	"fmt"
	"math"
	"os"
	"strconv"
)
 
const (
	MAXN    = 101
	MAXM    = 55001 // 50000(h) + 5000(val[i])
	MAX_INT = math.MaxInt
)
 
var (
	n      int // 公司数量
	h      int // 至少要买的干草数量
	maxVal int // val[i] 的最大值
	m      int // dp 表大小：h + maxVal
	cost   = [MAXN]int{}
	val    = [MAXN]int{}
	dp     = [MAXM]int{}
)
 
func main() {
	// s := `2 15
	// 3 2
	// 5 3`
	// in := bufio.NewScanner(strings.NewReader(s))
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		in.Scan()
		h, _ = strconv.Atoi(in.Text())
		maxVal = 0
		for i := 1; i <= n; i++ {
			in.Scan()
			val[i], _ = strconv.Atoi(in.Text())
			in.Scan()
			cost[i], _ = strconv.Atoi(in.Text())
			maxVal = max(maxVal, val[i])
		}
		// 最核心的一句，包含重要分析
		m = h + maxVal
		fmt.Fprintln(out, compute())
	}
	out.Flush()
}
 
func compute() int {
	// 初始化：
	// dp[0][0]: 0 家公司，买 0 数量干草，花费是 0
	dp[0] = 0
	// dp[0][1:m+1]: 0 家公司，买 j 数量干草，没办法买到，MAX_INT 代表无效方法
	for j := 1; j <= m; j++ {
		dp[j] = MAX_INT
	}
 
	for i := 1; i <= n; i++ {
		for j := val[i]; j <= m; j++ {
			if dp[j-val[i]] != MAX_INT { // 有效
				dp[j] = min( // min：求最小花费
					dp[j],                // dp[i-1][j]：不买 i 公司的，在前 i-1 家公司选
					dp[j-val[i]]+cost[i], // dp[i][j-val[i]] + cost[i]：买 i 公司的
				)
			}
		}
	}
 
	ans := MAX_INT
	for j := h; j <= m; j++ {
		ans = min(ans, dp[j])
	}
	return ans
}