前置知识:经典递归过程解析、从递归入手一维动态规划
本节课:
- 讲解从递归到二维动态规划的过程
- 讲解二维动态规划的空间压缩技巧
- 讲解哪些递归不适合或者说没有必要改成动态规划
下节课:直接从动态规划的定义入手,来见识更多二维动态规划问题
二维动态规划
尝试函数有一个可变参数可以完全决定返回值,进而可以改出一维动态规划表的实现
同理,尝试函数有两个可变参数可以完全决定返回值,那么就可以改出两维动态规划的实现
大体过程
一维、二维、三维甚至多维动态规划问题,大体过程都是:
- 写出尝试递归
- 记忆化搜索(从顶到底的动态规划,复杂 → 简单)
- 严格位置依赖的动态规划(从底到顶的动态规划,简单 → 复杂)
- 空间、时间的更多优化
复杂度和空间压缩技巧
动态规划表的大小:每个可变参数的可能性数量相乘
动态规划方法的时间复杂度:动态规划表的大小 * 每个格子的枚举代价
二维动态规划依然需要去整理动态规划表的格子之间的依赖关系
找寻依赖关系,往往通过画图来建立空间感,使其更显而易见
然后依然是从简单格子填写到复杂格子的过程,即严格位置依赖的动态规划(从底到顶)
二维动态规划的压缩空间技巧原理不难,会了之后千篇一律
但是不同题目依赖关系不一样,需要很细心的画图来整理具体题目的依赖关系,最后进行空间压缩的实现
什么样的递归可以改成动态规划?
能改成动态规划的递归,统一特征:
决定返回值的可变参数类型往往都比较简单,一般不会比 int 类型更复杂。为什么?
从这个角度,可以解释带路径的递归(即:回溯)(可变参数类型复杂),不适合或者说没有必要改成动态规划:
- 路径往往是整个表的状态
- 整个表的状态怎么表示?
- 就算能表示,情况那么多,动态规划表空间爆炸,时间也和动态规划表大小挂钩
题目 2 就是说明这一点的
一定要写出可变参数类型简单(不比 int 类型更复杂),并且可以完全决定返回值的递归,保证做到这些可变参数可以完全代表之前决策过程对后续过程的影响!再去改动态规划!
总结:
- 递归在展开计算时,总是重复调用同一个子问题的解
- 决定返回值的可变参数类型往往都比较简单
不管几维动态规划,经常从递归的定义出发,避免后续进行很多边界讨论,这需要一定的经验来预知
备注
二维动态规划问题非常多,不仅本节和 下节 涉及,整个系列课程会大量涉及
【必备】课程后续会讲背包 dp、区间 dp、状压 dp 等等,依然包含大量二维动态规划问题
题目1.最小路径和
二维动态规划入门
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
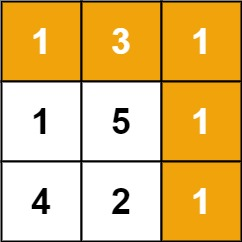
输入:
grid = [[1,3,1],[1,5,1],[4,2,1]]输出:
7解释:因为路径
1 → 3 → 1 → 1 → 1的总和最小。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
测试链接
暴力递归
var (
theGrid [][]int
)
func minPathSum(grid [][]int) int {
theGrid = grid
n := len(grid)
m := len(grid[0])
return f(n-1, m-1) // 递归逆推
}
func f(i, j int) int {
// base case
if i == 0 && j == 0 {
return theGrid[0][0]
}
up := math.MaxInt
left := math.MaxInt
if i-1 >= 0 {
// 向上
up = f(i-1, j)
}
if j-1 >= 0 {
// 向左
left = f(i, j-1)
}
return theGrid[i][j] + min(up, left)
}记忆化搜索
var (
theGrid [][]int
cache [][]int
)
func minPathSum(grid [][]int) int {
theGrid = grid
n := len(grid)
m := len(grid[0])
cache = make([][]int, n)
for i := range cache {
cache[i] = make([]int, m)
for j := 0; j < m; j++ {
cache[i][j] = -1
}
}
return f(n-1, m-1)
}
func f(i, j int) int {
if cache[i][j] != -1 {
return cache[i][j]
}
ans := 0
// base case
if i == 0 && j == 0 {
ans = theGrid[0][0]
} else {
up := math.MaxInt
left := math.MaxInt
if i-1 >= 0 {
// 向上
up = f(i-1, j)
}
if j-1 >= 0 {
// 向左
left = f(i, j-1)
}
ans = theGrid[i][j] + min(up, left)
}
cache[i][j] = ans
return ans
}位置依赖
func minPathSum(grid [][]int) int {
n := len(grid)
m := len(grid[0])
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, m)
}
dp[0][0] = grid[0][0]
for i := 1; i < n; i++ {
dp[i][0] = grid[i][0] + dp[i-1][0]
}
for j := 1; j < m; j++ {
dp[0][j] = grid[0][j] + dp[0][j-1]
}
for i := 1; i < n; i++ {
for j := 1; j < m; j++ {
dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
}
}
return dp[n-1][m-1]
}空间压缩 ^1
每个位置只依赖其上边单元格和左边单元格,运用滚动数组技巧,将二维 dp 数组压缩成一维
注意:只是对 dp 数组位置进行了复用,其整体思路和时间复杂度和二维 dp 数组是一样的
func minPathSum(grid [][]int) int {
n := len(grid)
m := len(grid[0])
dp := make([]int, m)
dp[0] = grid[0][0]
for j := 1; j < m; j++ {
dp[j] = grid[0][j] + dp[j-1]
}
for i := 1; i < n; i++ {
dp[0] += grid[i][0]
for j := 1; j < m; j++ {
// min(dp[j] /* 上 */, dp[j-1] /* 左 */)
dp[j] = grid[i][j] + min(dp[j], dp[j-1])
}
}
return dp[m-1]
}题目2.单词搜索
无法改成动态规划
题目描述
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
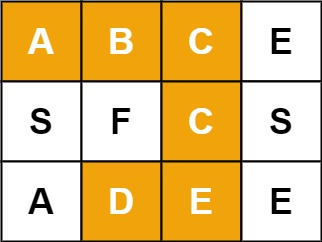
输入:
board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"输出:
true
提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board和word仅由大小写英文字母组成
测试链接
思路
要使用回溯算法,无法使用动态规划
答案
var (
theBoard [][]byte
theWord string
n int
m int
w int
)
func exist(board [][]byte, word string) bool {
theBoard = board
theWord = word
n = len(board)
m = len(board[0])
w = len(word)
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
if f(i, j, 0) {
return true
}
}
}
return false
}
// 从 board[i][j] 出发,匹配 word[i:]
func f(i, j, k int) bool {
if k == w {
return true
}
if i < 0 || i == n || j < 0 || j == m || theBoard[i][j] != theWord[k] {
return false
}
char := theBoard[i][j]
// 因为 board 会改其中的字符,用来标记哪些字符无法再用
// 所以带路径的递归(回溯)无法改成动态规划或者说没必要
// board 状态不是简单可变参数,强行建 dp 状态表会很大,会适得其反
// 甚至远远差于回溯
theBoard[i][j] = 0 // 在一次尝试中,防止重复使用
ans := f(i-1, j, k+1) ||
f(i+1, j, k+1) ||
f(i, j-1, k+1) ||
f(i, j+1, k+1)
theBoard[i][j] = char // 回溯状态,不要干扰下次尝试
return ans
}题目3.最长公共子序列
题目描述
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
测试链接
思路
暴力递归思路 1
以结尾下标为可变参数
var (
s1 string
s2 string
n1 int
n2 int
)
func longestCommonSubsequence(text1 string, text2 string) int {
s1 = text1
s2 = text2
n1 = len(text1)
n2 = len(text2)
return f(n1-1, n2-1)
}
// s1[:i1+1] 与 s2[:i2+1] 最长公共子序列长度
func f(i1, i2 int) int {
if i1 < 0 || i2 < 0 {
return 0
}
// 4 种情况
p1 := f(i1-1, i2-1) // i1 字符和 i2 字符都不要
p2 := f(i1-1, i2) // 不要 i1,要 i2
p3 := f(i1, i2-1) // 要 i1,不要 i2
p4 := 0
if s1[i1] == s2[i2] {
p4 = p1 + 1 // s1[i1] == s2[i2] 时,i1、i2 都要
}
return max(p1, p2, p3, p4)
}暴力递归思路 2
以子序列长度为可变参数
为了避免很多边界讨论,很多时候往往不用下标来定义尝试,而是用长度来定义尝试,因为长度最短是 0,而下标越界的话讨论起来就比较麻烦
var (
s1 string
s2 string
n1 int
n2 int
)
func longestCommonSubsequence(text1 string, text2 string) int {
s1 = text1
s2 = text2
n1 = len(text1)
n2 = len(text2)
return f(n1, n2)
}
// s1[前缀长度 len1] 与 s2[前缀长度 len2] 最长公共子序列长度
func f(len1, len2 int) int {
if len1 == 0 || len2 == 0 {
return 0
}
// 4 种情况没必要全部使用
// 情况 1 不可能比 2、3 好
// 情况 4 如果成立,则最好
ans := 0
if s1[len1-1] == s2[len2-1] {
// 情况 4 成立,情况 4 就是最佳选择
ans = f(len1-1, len2-1) + 1
} else {
// 情况 4 不成立,从情况 2、3 取较佳选择,情况 1 必定不比这个更好
ans = max(f(len1-1, len2), f(len1, len2-1))
}
return ans
}记忆化搜索
从 暴力递归思路 2 改成记忆化搜索,因为长度最短是 0,而下标越界的话缓存表建立比较麻烦
var (
s1 string
s2 string
n1 int
n2 int
cache [][]int
)
func longestCommonSubsequence(text1 string, text2 string) int {
s1 = text1
s2 = text2
n1 = len(text1)
n2 = len(text2)
cache = make([][]int, n1+1)
for i := range cache {
cache[i] = make([]int, n2+1)
for j := 0; j <= n2; j++ {
cache[i][j] = -1
}
}
return f(n1, n2)
}
// s1[前缀长度 len1] 与 s2[前缀长度 len2] 最长公共子序列长度
func f(len1, len2 int) int {
if cache[len1][len2] != -1 {
return cache[len1][len2]
}
ans := 0
if len1 == 0 || len2 == 0 {
ans = 0
} else if s1[len1-1] == s2[len2-1] {
ans = f(len1-1, len2-1) + 1
} else {
ans = max(f(len1-1, len2), f(len1, len2-1))
}
cache[len1][len2] = ans
return ans
}位置依赖
func longestCommonSubsequence(text1 string, text2 string) int {
n1 := len(text1)
n2 := len(text2)
dp := make([][]int, n1+1)
for i := range dp {
dp[i] = make([]int, n2+1)
}
// dp[0][*] 和 dp[*][0] 都是 0,就是初始化了
for len1 := 1; len1 <= n1; len1++ {
for len2 := 1; len2 <= n2; len2++ {
if text1[len1-1] == text2[len2-1] {
dp[len1][len2] = dp[len1-1][len2-1] + 1
} else {
dp[len1][len2] = max(dp[len1-1][len2], dp[len1][len2-1])
}
}
}
return dp[n1][n2]
}空间压缩 ^2
每个位置依赖左、上、左上三个位置,可以像 题目 1 一样使用滚动数组进行空间压缩,因为从左往右更新时,上一次会更新掉左上这个点的数据,所以要加一个 topLeft 变量记录
func longestCommonSubsequence(text1 string, text2 string) int {
n1 := len(text1)
n2 := len(text2)
if n1 < n2 {
n1, n2 = n2, n1
text1, text2 = text2, text1
}
// O(min(n1, n2))
dp := make([]int, n2+1)
for len1 := 1; len1 <= n1; len1++ {
topLeft, backup := 0, 0
for len2 := 1; len2 <= n2; len2++ {
backup = dp[len2]
if text1[len1-1] == text2[len2-1] {
dp[len2] = topLeft + 1
} else {
dp[len2] = max(dp[len2], dp[len2-1])
}
topLeft = backup
}
}
return dp[n2]
}题目4.最长回文子序列
题目描述
给你一个字符串 s,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
提示:
1 <= s.length <= 1000s仅由小写英文字母组成
测试链接
思路
转换成最长公共子序列问题
相当于求该串和其逆序串的 最长公共子序列
区间 dp
以 l、r 为字符串左右边界进行动态规划,有区间 dp 的雏形了
暴力递归
var (
S string
n int
)
func longestPalindromeSubseq(s string) int {
S = s
n = len(s)
return f(0, n-1)
}
// s[l:r+1] 最长回文子序列长度
// l <= r
func f(l, r int) int {
if l == r {
return 1
}
if l+1 == r {
if S[l] == S[r] {
return 2
} else {
return 1
}
}
if S[l] == S[r] {
return f(l+1, r-1) + 2
} else {
return max(f(l+1, r), f(l, r-1))
}
}位置依赖
func longestPalindromeSubseq(s string) int {
n := len(s)
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, n)
}
for l := n - 1; l >= 0; l-- { // 从下到上
dp[l][l] = 1 // 对角线
// l+1 == r 线
if l+1 < n {
if s[l] == s[l+1] {
dp[l][l+1] = 2
} else {
dp[l][l+1] = 1
}
}
// 其他位置
for r := l + 2; r < n; r++ { // 从左到右
if s[l] == s[r] {
dp[l][r] = dp[l+1][r-1] + 2
} else {
dp[l][r] = max(dp[l+1][r], dp[l][r-1])
}
}
}
return dp[0][n-1]
}空间压缩
func longestPalindromeSubseq(s string) int {
n := len(s)
dp := make([]int, n)
leftBottom, backup := 0, 0
for l := n - 1; l >= 0; l-- { // 从下到上
dp[l] = 1 // 对角线
// l+1 == r 线
if l+1 < n {
leftBottom = dp[l+1]
if s[l] == s[l+1] {
dp[l+1] = 2
} else {
dp[l+1] = 1
}
}
// 其他位置
for r := l + 2; r < n; r++ { // 从左到右
backup = dp[r]
if s[l] == s[r] {
dp[r] = leftBottom + 2
} else {
dp[r] = max(dp[r], dp[r-1])
}
leftBottom = backup
}
}
return dp[n-1]
}题目5.节点数为 n 高度不大于 m 的二叉树个数
题目描述
小强现在有 n 个节点,他想请你帮他计算出有多少种不同的二叉树满足节点个数为 n 且树的高度不超过 m 的方案
因为答案很大,所以答案需要模上 1e9+7 后输出
树的高度:定义为所有叶子到根路径上节点个数的最大值
示例 1:
输入:
n=3, m=3输出:
5
数据范围:1≤n,m≤50
进阶:时间复杂度 ,空间复杂度
测试链接
记忆化搜索
package main
import (
"bufio"
"fmt"
"os"
"strconv"
)
const (
MOD = 1e9 + 7
MAXN = 51
)
var (
n int
m int
cache = [MAXN][MAXN]int{}
)
func build() {
for i := 0; i <= n; i++ {
for j := 0; j <= m; j++ {
cache[i][j] = -1
}
}
}
// 记忆化搜索
func compute1(n, m int) int {
if n == 0 {
return 1 // 空树,一种方案
}
if m == 0 {
// 高度为 0,但还有节点,没有方案
return 0
}
if cache[n][m] != -1 {
return cache[n][m]
}
ans := 0
for k := 0; k < n; k++ {
// 一共 n 个节点,头节点已经占用了 1 个
// 如果左树占用 k 个,那么右树就占用 n-k-1 个
ans = (ans + compute1(k, m-1)*compute1(n-k-1, m-1)%MOD) % MOD
}
cache[n][m] = ans
return ans
}
func main() {
in := bufio.NewScanner(os.Stdin)
in.Split(bufio.ScanWords)
out := bufio.NewWriterSize(os.Stdout, 4096)
for in.Scan() {
n, _ = strconv.Atoi(in.Text())
in.Scan()
m, _ = strconv.Atoi(in.Text())
build()
fmt.Fprintln(out, compute1(n, m))
}
out.Flush()
}位置依赖
package main
import (
"bufio"
"fmt"
"os"
"strconv"
)
const (
MOD = 1e9 + 7
MAXN = 51
)
var (
n int
m int
dp = [MAXN][MAXN]int{}
)
// 严格位置依赖的动态规划
func compute2() int {
for j := 0; j <= m; j++ {
dp[0][j] = 1 // 空树,一种方案
}
for i := 1; i <= n; i++ {
dp[i][0] = 0 // 高度为 0,但还有节点,没有方案
for j := 1; j <= m; j++ {
dp[i][j] = 0
for k := 0; k < i; k++ {
// 一共 i 个节点,头节点已经占用了 1 个
// 如果左树占用 k 个,那么右树就占用 i-k-1 个
dp[i][j] = (dp[i][j] + dp[k][j-1]*dp[i-k-1][j-1]%MOD) % MOD
}
}
}
return dp[n][m]
}
func main() {
in := bufio.NewScanner(os.Stdin)
in.Split(bufio.ScanWords)
out := bufio.NewWriterSize(os.Stdout, 4096)
for in.Scan() {
n, _ = strconv.Atoi(in.Text())
in.Scan()
m, _ = strconv.Atoi(in.Text())
fmt.Fprintln(out, compute2())
}
out.Flush()
}空间压缩
每一个格子,都依赖前一列的上面所有格子
使用滚动数组技巧,dp 表压缩为一列,从左往右滚动过去
每次从下往上填新的格子,这样每个格子的依赖都是对的;如果从上往下就不对了(被更新掉了)
package main
import (
"bufio"
"fmt"
"os"
"strconv"
)
const (
MOD = 1e9 + 7
MAXN = 51
)
var (
n int
m int
dp = [MAXN]int{}
)
// 动态规划 + 空间压缩
func compute3() int {
dp[0] = 1 // 空树,一种方案
for i := 1; i <= n; i++ {
dp[i] = 0 // 高度为 0,但还有节点,没有方案
}
// 根据依赖,一定要先枚举列
for j := 1; j <= m; j++ { // 从左往右滚动过去
for i := n; i >= 1; i-- { // 从下往上填格子
dp[i] = 0
for k := 0; k < i; k++ {
dp[i] = (dp[i] + dp[k]*dp[i-k-1]%MOD) % MOD
}
}
}
return dp[n]
}
func main() {
in := bufio.NewScanner(os.Stdin)
in.Split(bufio.ScanWords)
out := bufio.NewWriterSize(os.Stdout, 4096)
for in.Scan() {
n, _ = strconv.Atoi(in.Text())
in.Scan()
m, _ = strconv.Atoi(in.Text())
fmt.Fprintln(out, compute3())
}
out.Flush()
}复杂度
- 时间复杂度:,其中 是 dp 表大小,每次枚举出一个 dp 格子的时间复杂度是
- 空间复杂度:
- 记忆化搜索、动态规划:
- 空间压缩:
题目6.矩阵中的最长递增路径
题目描述
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
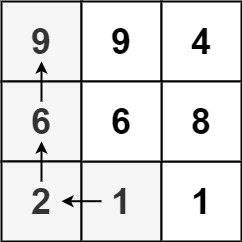
输入:
matrix = [[9,9,4],[6,6,8],[2,1,1]]输出:
4解释:最长递增路径为
[1, 2, 6, 9]。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 2^31 - 1
测试链接
思路
因为最长递增路径是严格递增的,所以都不需要判断节点是否使用过(使用过的节点必定不能满足严格递增)
该题写到记忆化搜索就行了,因为没有严格的依赖关系(依赖关系是小于当前数的位置,并不是严格的上下左右),不好改写也不必改写成动态规划
暴力递归
var (
theMatrix [][]int
n int
m int
)
func longestIncreasingPath(matrix [][]int) int {
ans := 0
theMatrix = matrix
n = len(matrix)
m = len(matrix[0])
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
ans = max(ans, f(i, j))
}
}
return ans
}
// 从 (i,j) 出发,能走出来多长的递增路径
func f(i, j int) int {
ans := 0
if i > 0 && theMatrix[i][j] < theMatrix[i-1][j] {
ans = max(ans, f(i-1, j))
}
if i+1 < n && theMatrix[i][j] < theMatrix[i+1][j] {
ans = max(ans, f(i+1, j))
}
if j > 0 && theMatrix[i][j] < theMatrix[i][j-1] {
ans = max(ans, f(i, j-1))
}
if j+1 < m && theMatrix[i][j] < theMatrix[i][j+1] {
ans = max(ans, f(i, j+1))
}
return ans + 1
}记忆化搜索
var (
theMatrix [][]int
n int
m int
cache [][]int
)
func longestIncreasingPath(matrix [][]int) int {
ans := 0
theMatrix = matrix
n = len(matrix)
m = len(matrix[0])
cache = make([][]int, n)
for i := range cache {
cache[i] = make([]int, m)
}
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
ans = max(ans, f(i, j))
}
}
return ans
}
// 从 (i,j) 出发,能走出来多长的递增路径
func f(i, j int) int {
if cache[i][j] != 0 {
return cache[i][j]
}
ans := 0
if i > 0 && theMatrix[i][j] < theMatrix[i-1][j] {
ans = max(ans, f(i-1, j))
}
if i+1 < n && theMatrix[i][j] < theMatrix[i+1][j] {
ans = max(ans, f(i+1, j))
}
if j > 0 && theMatrix[i][j] < theMatrix[i][j-1] {
ans = max(ans, f(i, j-1))
}
if j+1 < m && theMatrix[i][j] < theMatrix[i][j+1] {
ans = max(ans, f(i, j+1))
}
cache[i][j] = ans + 1
return ans + 1
}