三维物体是由二维图形（特别是三角形）组成的

视点和视线

三维物体与二维图形的最显著区别就是，三维物体具有深度，也就是 Z 轴

但是，最后还是得把三维场景绘制到二维的屏幕上，即绘制观察者看到的世界。观察者：在什么地方、朝哪里看、视野有多宽、能看多远

将观察者所处的位置称为视点（eye point）
从视点出发沿着观察方向的射线称作视线（viewing direction）

本节将研究如何通过视点和视线来描述观察者，到下一节再来研究“观察者能看多远”的问题

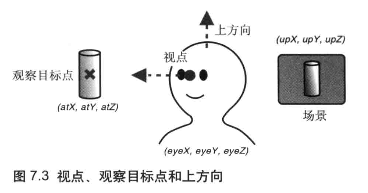
视点、观察目标点和上方向

为了确定观察者的状态，需要获取三项信息：

视点，即观察者的位置
- 视点坐标用 (eyeX, eyeY, eyeZ) 表示
观察目标点（look-at point），即被观察目标所在的点，可以用来确定视线
- 注意，观察目标点是一个点，而不是视线方向，只有同时知道观察目标点和视点，才能算出视线方向
- 观察目标点的坐标用 (atX, atY, atZ) 表示
上方向（up direction），即最终绘制在屏幕上的影像中的向上的方向
- 上方向是具有 3 个分量的矢量，用 (upX, upY, upZ) 表示

在 WebGL 中，可以用上述三个矢量创建一个视图矩阵（view matrix）用于表示观察者的状态，然后将该矩阵传给顶点着色器。之所以被称为视图矩阵，是因为它最终影响了显示在屏幕上的视图，也就是观察者观察到的场景

矩阵变换库 cuon-matrix.js 提供了方法可以根据上述三个矢量：视点、观察点、上方向，来创建出视图矩阵：Matrix4.setLookAt(eyeX, eyeY, eyeZ, atX, atY, atZ, upX, upY, upZ)，视图矩阵的类型是 Matrix4，其观察点映射到 <canvas> 的中心点

WebGL 系统中，观察者的默认状态：

视点处于原点 (0, 0, 0)
观察点为 (0, 0, 任意负值)，即视线为 Z 轴负方向（指向屏幕内部）
上方向 Y 轴正方向，即 (0, 1, 0)

使用视图矩阵

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_ViewMatrix; // 视图矩阵
varying vec4 v_Color;
void main() {
  gl_Position = u_ViewMatrix * a_Position;
  v_Color = a_Color;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
varying vec4 v_Color;
void main() {
  gl_FragColor = v_Color;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
 
// 设置顶点坐标和颜色
const n = initVertexBuffers(gl)
if (n < 0) {
console.error('设置顶点位置失败')
return
}
 
// 获取 u_ViewMatrix uniform 变量
const u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix')
if (!u_ViewMatrix) {
console.error('获取 uniform 变量失败')
return
}
 
// 定义视图矩阵：视点、目标点（视线）、上方向
const viewMatrix = new Matrix4()
viewMatrix.setLookAt(0.2, 0.25, 0.25, 0, 0, 0, 0, 1, 0)
 
// 将视图矩阵传给 u_ViewMatrix
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements)
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）
 
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 点的个数
  const n = 9
  // 三个点的坐标和颜色信息
  const verticesColors = new Float32Array([
    // 顶点坐标和颜色 (x, y, z, r, g, b)
    0.0, 0.5, -0.4, 0.0, 1.0, 0.0, // 绿色三角形在最后面
    -0.5, -0.5, -0.4, 0.0, 1.0, 0.0,
    0.5, -0.5, -0.4, 0.0, 1.0, 0.0,
 
    -0.5, 0.5, -0.2, 1.0, 0.0, 0.0, // 红色三角形在中间
    0.5, 0.5, -0.2, 1.0, 0.0, 0.0,
    0.0, -0.5, -0.2, 1.0, 0.0, 0.0,
 
    0.0, 0.5, 0.0, 0.0, 0.0, 1.0, // 蓝色三角形在最前面
    -0.5, -0.5, 0.0, 0.0, 0.0, 1.0,
    0.5, -0.5, 0.0, 0.0, 0.0, 1.0,
  ])
 
  // 创建缓冲区对象
  // 将缓冲区对象绑定到目标
  // 向缓冲区对象中写入数据
  // 获取 attribute 变量的存储位置
 
  // 将缓冲区对象分配给 attribute 变量
  const FSIZE = verticesColors.BYTES_PER_ELEMENT
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0)
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3)
 
  // 开启 attribute 变量与分配给它的缓冲区对象
}

可以看到这里的视图矩阵和之前的模型矩阵用法是一样的，都是 $< 顶点坐标 >=< 视图 / 模型矩阵 > \times < 原始顶点坐标 >$

这是因为“改变观察者的状态”与“对整个世界进行模型变换”，本质上是一样的，比如：

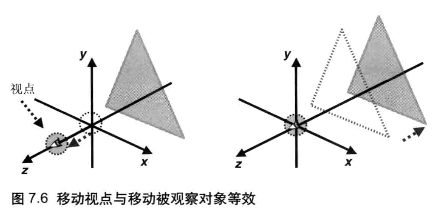
为了“语义化”，区分了视图矩阵和模型矩阵，可以这样使用： $< 顶点坐标 >=< 视图矩阵 > \times < 模型矩阵 > \times < 原始顶点坐标 >$

因为矩阵相乘符合结合律，所以上式等同于 $< 顶点坐标 >= (< 视图矩阵 > \times < 模型矩阵 >) \times < 原始顶点坐标 >$ ，将 $< 视图矩阵 > \times < 模型矩阵 >$ 得到的矩阵称为模型视图矩阵（model view matrix）

利用键盘改变视点

// 顶点着色器程序（GLSL ES）
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 u_ViewMatrix uniform 变量
// 定义视图矩阵：视点、目标点（视线）、上方向
// 将视图矩阵传给 u_ViewMatrix
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）
 
// 注册键盘事件
let eyeX = 0.2, eyeY = 0.25, eyeZ = 0.25
document.onkeydown = function (event) {
  switch (event.key) {
    case 'w':
    case 'ArrowUp':
      eyeY += 0.05
      break
    case 's':
    case 'ArrowDown':
      eyeY -= 0.05
      break
    case 'a':
    case 'ArrowLeft':
      eyeX -= 0.05
      break
    case 'd':
    case 'ArrowRight':
      eyeX += 0.05
      break
    case 'q':
      eyeZ -= 0.05
      break
    case 'e':
      eyeZ += 0.05
      break
    default:
      return
  }
 
  // 更新视图矩阵
  viewMatrix.setLookAt(eyeX, eyeY, eyeZ, 0, 0, 0, 0, 1, 0)
  // 将视图矩阵传给 u_ViewMatrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements)
  // 清空 canvas
  gl.clear(gl.COLOR_BUFFER_BIT)
  // 绘制图形（三角形）
  gl.drawArrays(gl.TRIANGLES, 0, n)
}

当视点移动时，三角形可能缺少一部分：

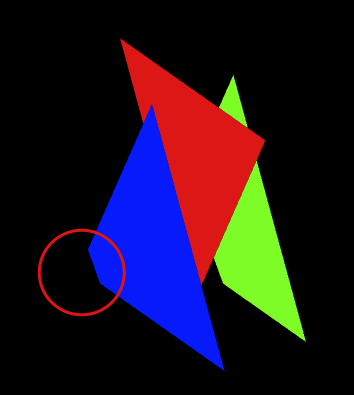
这是因为没有指定可视范围（visible range），即实际观察得到的区域边界。WebGL 只显示可视范围内的区域。例中当改变视点位置时，三角形的一部分到了可视范围外，就缺了一个角

可视范围

虽然可以将三维物体放在三维空间中的任何地方，但是只有当它在可视范围内时，WebGL 才会绘制它。事实上，不绘制可视范围外的对象，是基本的降低程序开销的手段。绘制可视范围外的对象没有意义，即使把它们绘制出来也不会在屏幕上显示

可视范围在 WebGL 中称为可视空间（view volume），包括：

水平视角
垂直视角
可视深度

可视空间

有两类常用的可视空间：

长方体可视空间，也称盒状空间，由正射投影（orthographic projection）产生
- 正射投影的好处是用户可以方便地比较场景中物体（如：原子模型）的大小，这是因为物体看上去的大小与其所在的位置没有关系
- 在建筑平面图等技术绘图的相关场合，应当使用正射投影
四棱锥/金字塔可视空间，由透视投影（perspective projection）产生
- 在透视投影下，产生的三维场景看上去更是有深度感，更加自然（“近大远小”），因为我们平时观察真实世界用的也是透视投影
- 在大多数情况下，比如三维射击类游戏中，都应当采用透视投影

定义盒状可视空间（正射投影）

正射投影的盒状可视空间可视空间由前后两个矩形表面确定，分别称近裁剪面和远裁剪面：

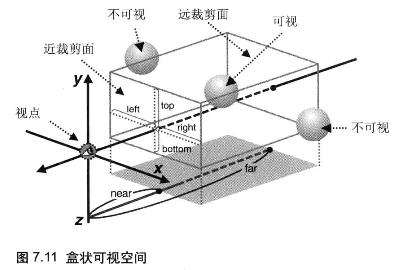
<canvas> 上显示的就是可视空间中物体在近裁剪面上的投影，如果裁剪面的宽高比和 <canvas> 不一样，那么画面就会被按照 <canvas> 的宽高比进行压缩，物体会被扭曲（详见）

近裁剪面与远裁剪面之间的盒形空间就是可视空间，只有在此空间内的物体会被显示出来。如果某个物体一部分在可视空间内，一部分在其外，那就只显示空间内的部分

矩阵变换库 cuon-matrix.js 提供了方法可以根据上图中六个浮点数，来创建出正射投影矩阵（orthographic projection matrix），正射投影矩阵的类型是 Matrix4

Matrix4.setOrtho(left, right, bottom, top, near, far)：

left, right, bottom, top：指定近裁剪面（远裁剪面也一样，也就是可视空间）的左、右、下、上边界
near, far：指定近裁剪面和远裁剪面的位置，也就是可视空间的近边界和远边界
注意：
- left, right 不一定相等，bottom, top 不一定相等
- left 不一定小于 right，大小情况不同决定了视点方向，bottom, top 同理
- near, far 必须不等，大小没限制，较大的那个被认为是远裁剪面

补上缺掉的角

之前当视点移动时三角形可能缺少一角，因为三角形的一部分位于可视区域之外，被裁剪掉了。现在来修复这个问题：适当地设置可视空间，确保三角形不被裁剪

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_ViewMatrix; // 视图矩阵
uniform mat4 u_ProjMatrix; // 投影矩阵
varying vec4 v_Color;
void main() {
  gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;
  v_Color = a_Color;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
varying vec4 v_Color;
void main() {
  gl_FragColor = v_Color;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 uniform 变量
 
// 定义视图矩阵：视点、目标点（视线）、上方向
const viewMatrix = new Matrix4()
viewMatrix.setLookAt(0.2, 0.25, 0.25, 0, 0, 0, 0, 1, 0)
 
// 定义投影矩阵：left, right, bottom, top, near, far
const projMatrix = new Matrix4()
projMatrix.setOrtho(-1.0, 1.0, -1.0, 1.0, -5.0, 5.0)
 
// 将视图矩阵和投影矩阵传给 uniform 变量
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements)
gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements)
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）
// 注册键盘事件

这样的可视空间足够大，无论如何移动视点，三角形都在可视空间内，不会被裁剪

顶点坐标计算公式： $< 顶点坐标 >=< 投影矩阵 > \times < 视图矩阵 > \times < 模型矩阵 > \times < 原始顶点坐标 >$

裁剪面宽高比和 `<canvas>` 宽高比

之前提过，如果可视空间近裁剪面的宽高比与 <canvas> 不一致，显示出的物体就会被压缩变形

将近裁剪面的宽度和高度改为了原来的一半，但是保持了宽高比：三角形变成了之前大小的两倍
- 这是由于 <canvas> 的大小没有发生变化，但是它表示的可视空间却缩小了一半
- 注意，三角形的有些部分越过了可视空间并被裁剪了
近裁剪面的宽度缩小而高度不变，没有保持宽高比：三角形在宽度上被拉伸变形
- 这是由于近裁剪面宽度缩小而高度不变，相当于把长方形的近裁剪面映射到了正方形的 <canvas> 上

定义四棱锥形可视空间（透视投影）

透视投影的四棱锥形可视空间就像盒状可视空间那样，也有视点、视线、近裁剪面和远裁剪面。可视空间内的物体才会被显示，可视空间外的物体则不会显示，那些跨越可视空间边界的物体则只会显示其在可视空间内的部分

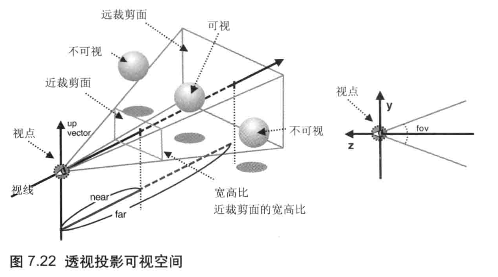
矩阵变换库 cuon-matrix.js 同样提供了方法来创建出透视投影矩阵（perspective projection matrix），透视投影矩阵的类型也是 Matrix4

Matrix4.setPerspective(fov, aspect, near, far)：

fov：指定垂直视角，即可视空间顶点和底面的夹角，必须大于 0
aspect：指定近裁剪面的宽高比（宽度 / 高度）
near, far：指定近裁剪面和远裁剪面的位置，也就是可视空间的近边界和远边界（near 必须小于 far，且两者必须都大于 0）

其中，第 2 个参数 aspect 宽高比（近裁剪面的宽度与高度的比值）应当与 <canvas> 保持一致，否则也会导致显示出来的图形变形

示例程序

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_ViewMatrix; // 视图矩阵
uniform mat4 u_ProjMatrix; // 投影矩阵
varying vec4 v_Color;
void main() {
  gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;
  v_Color = a_Color;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
varying vec4 v_Color;
void main() {
  gl_FragColor = v_Color;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 uniform 变量
 
// 定义视图矩阵：视点、目标点（视线）、上方向
const viewMatrix = new Matrix4()
viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0)
 
// 定义投影矩阵：left, right, bottom, top, near, far
const projMatrix = new Matrix4()
projMatrix.setPerspective(30, canvas.width / canvas.height, 1, 100)
 
// 将视图矩阵和投影矩阵传给 uniform 变量
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 点的个数
  const n = 18
  // 三个点的坐标和颜色信息
  const verticesColors = new Float32Array([
    // 顶点坐标和颜色 (x, y, z, r, g, b)
  
    // 右侧的 3 个三角形
    0.75, 1.0, -4.0, 0.4, 1.0, 0.4, // 绿色三角形在最后面
    0.25, -1.0, -4.0, 0.4, 1.0, 0.4,
    1.25, -1.0, -4.0, 1.0, 0.4, 0.4,
  
    0.75, 1.0, -2.0, 1.0, 1.0, 0.4, // 黄色三角形在中间
    0.25, -1.0, -2.0, 1.0, 1.0, 0.4,
    1.25, -1.0, -2.0, 1.0, 0.4, 0.4,
  
    0.75, 1.0, 0.0, 0.4, 0.4, 1.0, // 蓝色三角形在最前面
    0.25, -1.0, 0.0, 0.4, 0.4, 1.0,
    1.25, -1.0, 0.0, 1.0, 0.4, 0.4,
  
    // 左侧的 3 个三角形
    -0.75, 1.0, -4.0, 0.4, 1.0, 0.4, // 绿色三角形在最后面
    -1.25, -1.0, -4.0, 0.4, 1.0, 0.4,
    -0.25, -1.0, -4.0, 1.0, 0.4, 0.4,
    
    -0.75, 1.0, -2.0, 1.0, 1.0, 0.4, // 黄色三角形在中间
    -1.25, -1.0, -2.0, 1.0, 1.0, 0.4,
    -0.25, -1.0, -2.0, 1.0, 0.4, 0.4,
    
    -0.75, 1.0, 0.0, 0.4, 0.4, 1.0, // 蓝色三角形在最前面
    -1.25, -1.0, 0.0, 0.4, 0.4, 1.0,
    -0.25, -1.0, 0.0, 1.0, 0.4, 0.4,
  ])
 
  // 创建缓冲区对象
  // 将缓冲区对象绑定到目标
  // 向缓冲区对象中写入数据
  // 获取 attribute 变量的存储位置
  // 将缓冲区对象分配给 attribute 变量
  // 开启 attribute 变量与分配给它的缓冲区对象
}

这里是将 $< 投影矩阵 > \times < 视图矩阵 > \times < 模型矩阵 >$ 放到着色器中计算，其实也可以通过 JS 计算，然后只需给着色器传入一个矩阵，称为模型视图投影矩阵（model view projection matrix）：

const modelMatrix = new Matrix4() // 模型矩阵
const viewMatrix = new Matrix4() // 视图矩阵
const projMatrix = new Matrix4() // 投影矩阵
const mvpMatrix = new Matrix4() // 模型视图投影矩阵
 
modelMatrix.setTranslate(0.75, 0, 0)
viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0)
projMatrix.setPerspective(30, canvas.width / canvas.height, 1, 100)
 
// 计算模型视图投影矩阵
mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix)

投影矩阵的作用

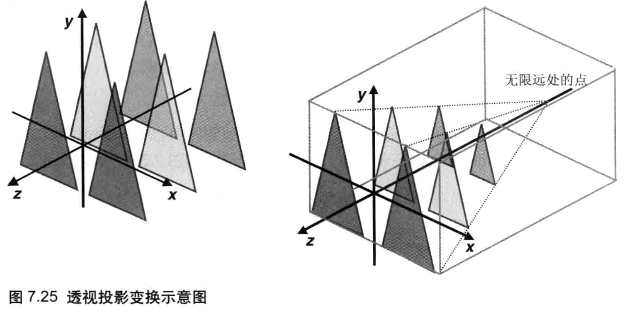
实际上，这些三角形的大小和 x、y 坐标是完全相同的，但是运用透视投影矩阵后，透视投影矩阵对三角形进行了两次变换：

根据三角形与视点的距离，按比例对三角形进行了缩小变换
对三角形进行平移变换，使其贴近视线

这表明，可视空间的规范可以用一系列基本变换来定义

换一个角度来看，透视投影矩阵实际上将金字塔状的可视空间变换为了盒状的可视空间，这个盒状的可视空间又称规范立方体（Canonical View Volume），正射投影矩阵的工作是将顶点从盒状的可视空间映射到规范立方体中。顶点着色器输出的顶点都必须在规范立方体中，这样才会显示在屏幕上

一个三角形多次渲染

上面代码的一个问题是，用了一大段枯燥的代码来定义所有顶点和颜色的数据，还仅仅只有 6 个三角形，如果三角形的数量进一步增加的话，那可真就是一团糟了

一个更好的方式是只提供必要的数据，然后将其进行变换并绘制（不清除之前的绘制）。如下提供了 1 个三角形的数据，对其进行了 6 次绘制：

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
uniform mat4 u_ModelMatrix; // 模型矩阵
uniform mat4 u_ViewMatrix; // 视图矩阵
uniform mat4 u_ProjMatrix; // 投影矩阵
void main() {
  gl_Position = u_ProjMatrix * u_ViewMatrix * u_ModelMatrix * a_Position;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
uniform vec4 u_FragColor; // 颜色
void main() {
  gl_FragColor = u_FragColor;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
 
// 获取 uniform 变量
const u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix')
const u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix')
const u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix')
const u_FragColor = gl.getUniformLocation(gl.program, 'u_FragColor')
if (!u_ModelMatrix || !u_ViewMatrix || !u_ProjMatrix || !u_FragColor) {
  console.error('获取 uniform 变量失败')
  return
}
 
// 定义模型矩阵
const modelMatrix = new Matrix4()
 
// 定义视图矩阵：视点、目标点（视线）、上方向
const viewMatrix = new Matrix4()
viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0)
 
// 定义投影矩阵：left, right, bottom, top, near, far
const projMatrix = new Matrix4()
projMatrix.setPerspective(30, canvas.width / canvas.height, 1, 100)
 
// 将视图矩阵和投影矩阵传给 uniform 变量
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements)
gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements)
 
// 设置清除颜色并清空 canvas
 
const colors = [
  [1.0, 0.0, 0.0],
  [0.0, 1.0, 0.0],
  [0.0, 0.0, 1.0],
]
 
// 左侧 3 个三角形
for (let i = 0; i < 3; i++) {
  modelMatrix.setTranslate(-0.75, 0, (2 - i) * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}
// 右侧 3 个三角形
for (let i = 0; i < 3; i++) {
  modelMatrix.setTranslate(0.75, 0, (2 - i) * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 点的个数
  const n = 3
  // 三个点的坐标信息
  const vertices = new Float32Array([
    0.0, 1.0, // 第一个点
    -0.5, -1.0, // 第二个点
    0.5, -1.0 // 第三个点
  ])
 
  // 创建缓冲区对象
  // 将缓冲区对象绑定到目标
  // 向缓冲区对象中写入数据
  // 获取 attribute 变量的存储位置
 
  // 将缓冲区对象分配给 attribute 变量
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
 
  // 开启 attribute 变量与分配给它的缓冲区对象
}

正确处理对象的前后关系

到目前为止，你已经能够编写代码移动视点、设置可视空间、从不同的角度观察三维对象。但是仍然还存在一个问题：在移动视点的过程中，有时候前面的三角形会“躲”到后面的三角形之后

这是因为 WebGL 在默认情况下会按照缓冲区中的顺序绘制图形，而且后绘制的图形覆盖先绘制的图形，因为这样做很高效（前面所有的示例都是故意先定义远的物体，后定义近的物体，从而产生正确的效果）

将之前的代码修改一下就很容易看出来了：

// 左侧 3 个三角形
for (let i = 0; i < 3; i++) {
  // 将 (2 - i) * -2 改成 i * -2
  // 就会出现近处三角形被远处三角形挡住的问题
  modelMatrix.setTranslate(-0.75, 0, i * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}
// 右侧 3 个三角形
for (let i = 0; i < 3; i++) {
  modelMatrix.setTranslate(0.75, 0, (2 - i) * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}

隐藏面消除（深度测试）

这样的做法（故意先定义远的物体，后定义近的物体，从而产生正确的效果），如果场景中的对象不发生运动，观察者的状态也是唯一的，那么没有问题。但是如果希望不断移动视点，从不同的角度看物体，那么不可能事先决定对象出现的顺序

为了解决这个问题，WebGL 提供了隐藏面消除（hidden surface removal）功能，这个功能会帮助我们消除那些被遮挡的表面（隐藏面），可以放心地绘制场景而不必顾及各物体在缓冲区中的顺序，因为远处的物体会自动被近处的物体挡住，不会被绘制出来

开启隐藏面消除（深度测试）功能，需要遵循以下两步：

开启深度测试功能：gl.enable(gl.DEPTH_TEST)
在绘制之前，清除深度缓冲区：gl.clear(gl.DEPTH_BUFFER_BIT)

gl.enable(cap)：开启 WebGL 的功能
- cap：指定需要开启的功能，可取：
  - gl.DEPTH_TEST：隐藏面消除（深度测试）
  - gl.BLEND：混合
  - gl.POLYGON_OFFSET_FILL：多边形偏移
  - 还有一些取值，本书不会设计，如 gl.CULL_FACE、gl.DITHER、gl.SAMPLE_ALPHA_TO_COVERAGE、gl.SAMPLE_COVERAGE、gl.SCISSOR_TEST、gl.STENCIL_TEST 等
- 错误
  - INVALID_ENUM：cap 的值无效
gl.disable(cap)：禁用 WebGL 的功能
- 参数、错误同 gl.enable(cap)
gl.clear(buffer)：清除缓冲区（详见）

深度缓冲区是一个中间对象，其作用是帮助 WebGL 进行隐藏面消除。WebGL 在颜色缓冲区中绘制几何图形，绘制完成后将颜色缓冲区显示到 <canvas> 上。如果要将隐藏面消除，那就必须知道每个几何图形的深度信息，而深度缓冲区就是用来存储深度信息的。由于深度方向通常是 Z 轴方向，所以有时候称其为 Z 缓冲区

在绘制任意一帧之前，都必须清除深度缓冲区，以消除绘制上一顿时在其中留下的痕迹。如果不这样做，就会出现错误的结果

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
uniform mat4 u_ModelMatrix; // 模型矩阵
uniform mat4 u_ViewMatrix; // 视图矩阵
uniform mat4 u_ProjMatrix; // 投影矩阵
void main() {
  gl_Position = u_ProjMatrix * u_ViewMatrix * u_ModelMatrix * a_Position;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
uniform vec4 u_FragColor; // 颜色
void main() {
  gl_FragColor = u_FragColor;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 uniform 变量
// 定义模型矩阵
// 定义视图矩阵：视点、目标点（视线）、上方向
// 定义投影矩阵：left, right, bottom, top, near, far
// 将视图矩阵和投影矩阵传给 uniform 变量
 
// 设置清除颜色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 开启深度测试
gl.enable(gl.DEPTH_TEST)
// 清除颜色缓冲区和深度缓冲区
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)
 
const colors = [
  [1.0, 0.0, 0.0],
  [0.0, 1.0, 0.0],
  [0.0, 0.0, 1.0],
]
 
// 左侧 3 个三角形
for (let i = 0; i < 3; i++) {
  // 开启深度测试后
  // 就不会出现近处三角形被远处三角形挡住的问题
  modelMatrix.setTranslate(-0.75, 0, i * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}
// 右侧 3 个三角形
for (let i = 0; i < 3; i++) {
  modelMatrix.setTranslate(0.75, 0, (2 - i) * -2)
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
  gl.uniform4f(u_FragColor, ...colors[i], 1.0)
  gl.drawArrays(gl.TRIANGLES, 0, n)
}

深度冲突

隐藏面消除是 WebGL 的一项复杂而又强大的特性，在绝大多数情况下，它都能很好地完成任务。然而，当几何图形或物体的两个表面极为接近时，就会出现新的问题，使得表面看上去斑斑驳驳的，这种现象被称为深度冲突（Z fighting）

之所以会产生深度冲突，是因为两个表面过于接近，深度缓冲区有限的精度已经不能区分哪个在前、哪个在后了。如果创建三维模型阶段就对顶点的深度值加以注意，是能够避免深度冲突的，但是，当场景中有多个运动着的物体时，实现这一点几乎是不可能的

WebGL 提供一种被称为多边形偏移（polygon offset）的机制来解决这个问题。该机制将自动在 Z 值加上一个偏移量，偏移量的值由物体表面相对于观察者视线的角度来确定。启用该机制需要两步：

开启多边形偏移功能：gl.enable(gl.POLYGON_OFFSET_FILL)
在绘制之前指定用来计算偏移量的参数：gl.polygonOffset(1.0, 1.0)

gl.polygonOffset(factor, units)：指定加到每个顶点绘制后 Z 值上的偏移量，偏移量按照公式 m * factor + r * units 计算，其中 m 表示顶点所在表面相对于观察者的视线的角度，r 表示硬件能够区分两个 Z 值之差的最小值

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_MvpMatrix;
varying vec4 v_Color;
void main() {
  gl_Position = u_MvpMatrix * a_Position;
  v_Color = a_Color;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
varying vec4 v_Color;
void main() {
  gl_FragColor = v_Color;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 uniform 变量
// 将 mvp 矩阵传给 uniform 变量
// 设置清除颜色
// 开启深度测试
// 清除颜色缓冲区和深度缓冲区
 
// 启用多边形偏移功能
gl.enable(gl.POLYGON_OFFSET_FILL)
 
// 绘制图形（三角形）
gl.drawArrays(gl.TRIANGLES, 0, n / 2) // 绘制绿色三角形
gl.polygonOffset(1.0, 1.0) // 设置多边形偏移参数
gl.drawArrays(gl.TRIANGLES, n / 2, n / 2) // 绘制黄色三角形
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 点的个数
  const n = 6
  // 三个点的坐标和颜色信息
  const verticesColors = new Float32Array([
    // 顶点坐标和颜色 (x, y, z, r, g, b)
    0.0, 2.5, -5.0, 0.0, 1.0, 0.0, // 绿色三角形
    -2.5, -2.5, -5.0, 0.0, 1.0, 0.0,
    2.5, -2.5, -5.0, 1.0, 0.0, 0.0,
  
    0.0, 3.0, -5.0, 1.0, 0.0, 0.0, // 黄色三角形
    -3.0, -3.0, -5.0, 1.0, 1.0, 0.0,
    3.0, -3.0, -5.0, 1.0, 1.0, 0.0
  ])
 
  // 创建缓冲区对象
  // 将缓冲区对象绑定到目标
  // 向缓冲区对象中写入数据
  // 获取 attribute 变量的存储位置
  // 将缓冲区对象分配给 attribute 变量
  // 开启 attribute 变量与分配给它的缓冲区对象
}

所有顶点的 Z 坐标值都一样（-0.5），但是没有出现深度冲突现象。先画了一个绿色三角形，然后通过设置了多边形偏移参数，使之后的绘制受到多边形偏移机制影响，再画了一个黄色三角形

立方体

如果使用 gl.drawArrays() 来绘制立方体：

gl.TRIANGLES：一个面的 2 个三角形需要 6 个顶点信息，6 个面共需要 $6 \times 6 = 36$ 个顶点信息
gl.TRIANGLE_FAN：一个面的 2 个三角形需要 4 个顶点信息，6 个面共需要 $4 \times 6 = 24$ 个顶点信息
- 但是，如果这样做就必须为每个面调用一次 gl.drawArrays()，一共 6 次调用
gl.TRIANGLE_STRIP：需要 14 个顶点信息

WebGL 提供了一种更好的方案 : gl.drawElements()，使用该函数替代 gl.drawArrays() 进行绘制，能够避免重复定义顶点，保持顶点数量最小

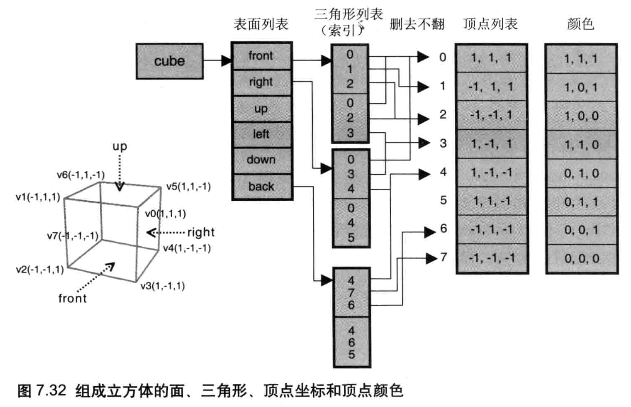
一个立方体有 6 个面，每个面有 2 个三角形，每个三角形有 3 个顶点。只需要定义 8 个顶点信息，再将每个面与 4 个顶点建立关系即可：

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
attribute vec4 a_Color;
uniform mat4 u_MvpMatrix;
varying vec4 v_Color;
void main() {
  gl_Position = u_MvpMatrix * a_Position;
  v_Color = a_Color;
}
`
 
// 片元着色器程序（GLSL ES）
const fragmentShaderSource = `
precision mediump float;
varying vec4 v_Color;
void main() {
  gl_FragColor = v_Color;
}
`
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点坐标和颜色
// 获取 uniform 变量
 
const mvpMatrix = new Matrix4()
mvpMatrix.setPerspective(30, canvas.width / canvas.height, 1, 100)
mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0)
 
// 将 mvp 矩阵传给 uniform 变量
// 设置清除颜色
// 开启深度测试
// 清除颜色缓冲区和深度缓冲区
 
// 绘制图形（立方体）
gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0)
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 8 个顶点坐标和颜色
  const verticesColors = new Float32Array([
    // 顶点坐标和颜色 (x, y, z, r, g, b)
    1, 1, 1, 1, 1, 1, // v0 白色
    -1, 1, 1, 1, 0, 1, // v1 品红色
    -1, -1, 1, 1, 0, 0,// v2 红色
    1, -1, 1, 1, 1, 0, // v3 黄色
    1, -1, -1, 0, 1, 0, // v4 绿色
    1, 1, -1, 0, 0, 1, // v5 青色
    -1, 1, -1, 0, 0, 1, // v6 蓝色
    -1, -1, -1, 0, 0, 0, // v7 黑色
  ])
  // 6 个面的顶点索引
  const indices = new Uint8Array([
    0, 1, 2, 0, 2, 3, // 前
    0, 3, 4, 0, 4, 5, // 右
    0, 5, 6, 0, 6, 1, // 上
    1, 6, 7, 1, 7, 2, // 左
    7, 4, 3, 7, 3, 2, // 下
    4, 7, 6, 4, 6, 5, // 后
  ])
 
  // 创建缓冲区对象
  const vertexColorBuffer = gl.createBuffer()
  const indexBuffer = gl.createBuffer()
  if (!vertexColorBuffer || !indexBuffer) {
    console.error('创建缓冲区对象失败')
    return -1
  }
 
  // 将顶点坐标和颜色写入缓冲区对象
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer)
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW)
 
  // 获取 attribute 变量的存储位置
  // 将缓冲区对象分配给 attribute 变量
  // 开启 attribute 变量与分配给它的缓冲区对象
 
  // 将顶点索引数据写入缓冲区
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer)
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW)
 
  return indices.length
}

通过顶点索引绘制物体

使用 gl.drawElements() 时，需要在 gl.ELEMENT_ARRAY_BUFFER（而不是 ARRAY_BUFFER，详见）中指定顶点的索引值，它管理着具有索引结构的三维模型数据

gl.drawElements(mode, count, type, offset)

mode：绘制的方式，详见
count：整型数，绘制顶点的个数，即：顶点索引数组的长度，顶点着色器的执行次数
type：索引值的数据类型，可取：
- gl.UNSIGNED_BYTE：索引数据的类型是 Uint8Array
- gl.UNSIGNED_SHORT：索引数据的类型是 Uint16Array
offset：指定索引数组中开始绘制的位置，以字节为单位
错误
- INVALID_ENUM：传入的 mode 参数不是前述参数之一
- INVALID_VALUE：参数 count 或 offset 是负数

向缓冲区中写入顶点的坐标、颜色与索引

在 gl.ARRAY_BUFFER 绑定的缓存区写入顶点坐标、颜色信息
在 gl.ELEMENT_ARRAY_BUFFER 绑定的缓存区写入顶点索引信息

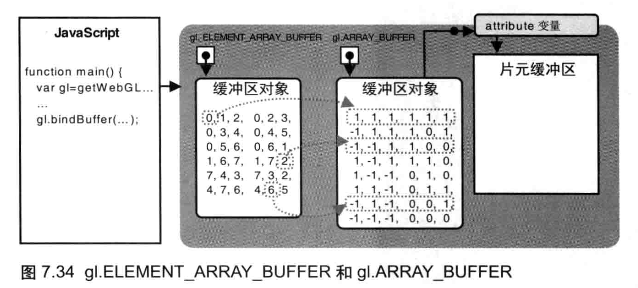
在调用 gl.drawElements() 时，WebGL 首先从绑定到 gl.ELEMENT_ARRAY_BUFFER 的缓冲区中获取顶点的索引值，然后根据该索引值，从绑定到 gl.ARRAY_BUFFER 的缓冲区中获取顶点的坐标、颜色等信息，然后传递给 attribute 变量并执行顶点着色器。对每个索引值都这样做，最后就绘制出了整个立方体

注意，颜色是依赖于顶点的，而一个顶点由三个面共用，考虑这样的情况：希望立方体的每个表面都是不同的单一颜色（或纹理图形），现在是做不到的

为了解决这个问题，需要创建多个具有相同坐标（而颜色值不同）的顶点，分开处理

My-Notes

全部文章

007.进入三维世界

视点和视线

视点、观察目标点和上方向

使用视图矩阵

利用键盘改变视点

可视范围

可视空间

定义盒状可视空间（正射投影）

补上缺掉的角

裁剪面宽高比和 `<canvas>` 宽高比

定义四棱锥形可视空间（透视投影）

示例程序

投影矩阵的作用

一个三角形多次渲染

正确处理对象的前后关系

隐藏面消除（深度测试）

深度冲突

立方体

通过顶点索引绘制物体

向缓冲区中写入顶点的坐标、颜色与索引

目录

反向链接

关系图谱

My-Notes

全部文章

007.进入三维世界

视点和视线

视点、观察目标点和上方向

使用视图矩阵

利用键盘改变视点

可视范围

可视空间

定义盒状可视空间（正射投影）

补上缺掉的角

裁剪面宽高比和 <canvas> 宽高比

定义四棱锥形可视空间（透视投影）

示例程序

投影矩阵的作用

一个三角形多次渲染

正确处理对象的前后关系

隐藏面消除（深度测试）

深度冲突

立方体

通过顶点索引绘制物体

向缓冲区中写入顶点的坐标、颜色与索引

目录

反向链接

关系图谱

裁剪面宽高比和 `<canvas>` 宽高比