010.决策树

决策树

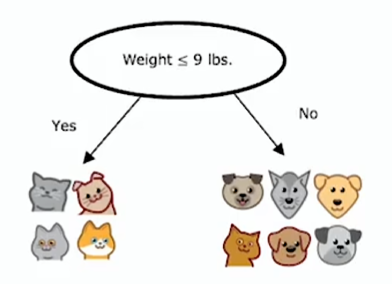
为解释决策树的工作方式，将以一个猫咪分类的例子作为示例贯穿讲解：你运营一家猫咪领养中心，并拥有一些特征数据，想训练一个分类器来快速判断一只动物是否为猫

训练决策树学习算法后可能得到：

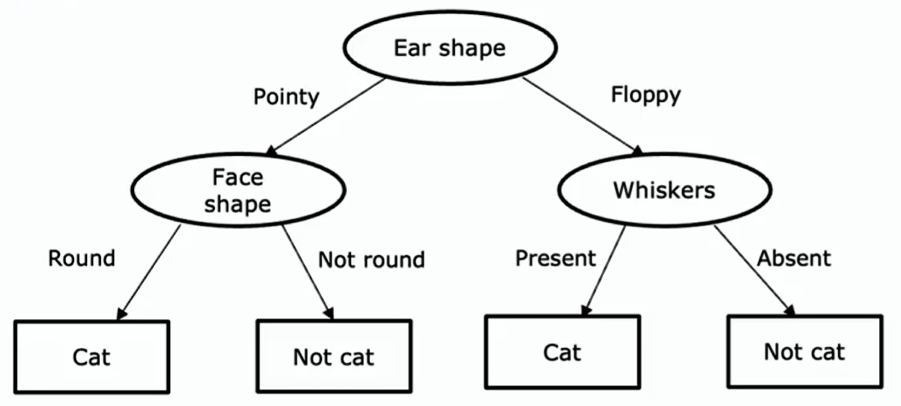
• 根节点（root node）：树中的最顶层的节点，图中 Ear shape 节点
• 决策节点（decision nodes）：图中椭圆形节点
  • 决策节点会查看特定特征，然后根据特征值决定沿树向左还是向右分支
• 叶节点（leaf nodes）：图中底部的矩形框节点，它们会做出预测

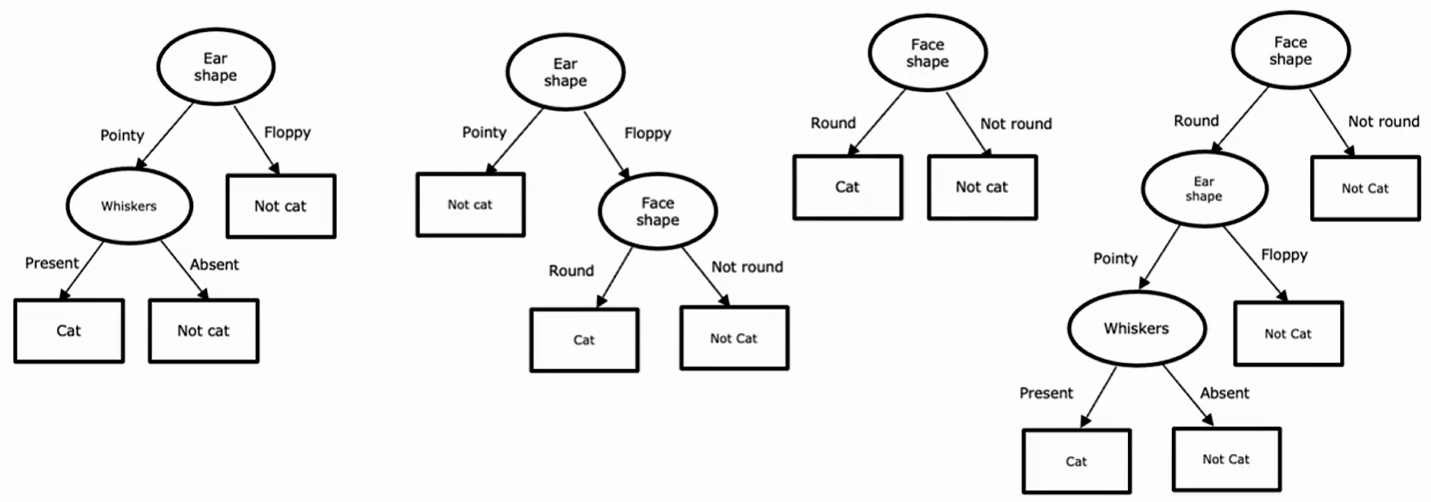
还有其他很多不同的决策树，在这些各异的决策树当中，有的表现好、有的表现差，决策树学习算法的任务是从所有可能的决策树里，试着选出一个有望在训练集上表现出色的一个，而且理想情况下，对新数据（交叉验证集和测试集）的泛化能力也强

学习过程

给定一个包含 10 个猫和狗示例的训练集，决策树学习过程：

1. 决定在根节点使用什么特征
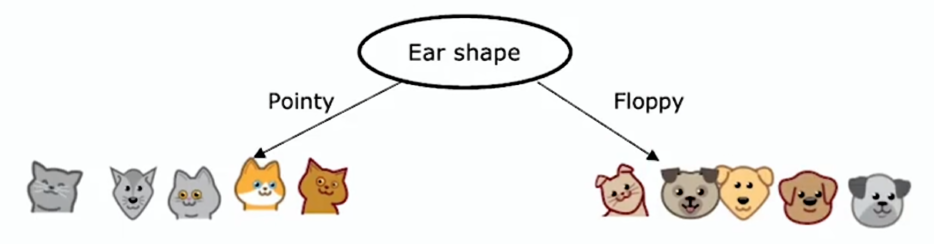
   • 假设决定选取耳朵形状特征作为根节点处的特征
   • 这意味着查看所有的训练样本，并依据耳朵形状特征的值对它们进行拆分
2. 聚焦于决策树的左分支，决定要依据什么特征来划分
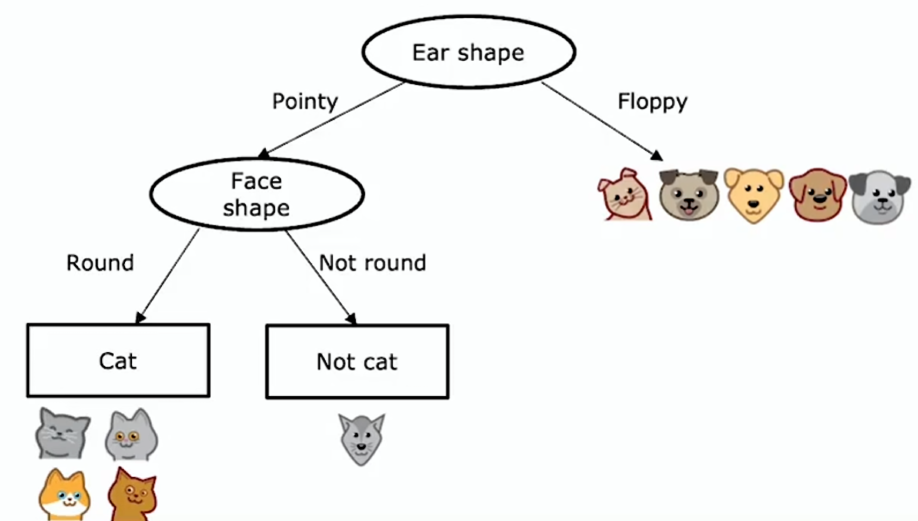
   • 假设决定在那儿使用脸型特征
   • 这意味着查看当前分支的训练样本，并依据脸型特征的值对它们进行拆分
   • 最后发现左分支四个例子都是猫，所以不再进一步划分，而是创建一个叶节点，预测到达这个节点的都是猫
   • 而右分支没有一个猫，就创建一个叶节点，预测到达这个节点的都不是猫
3. 在决策树的右分支重复同样的操作，直到创建所有的叶节点

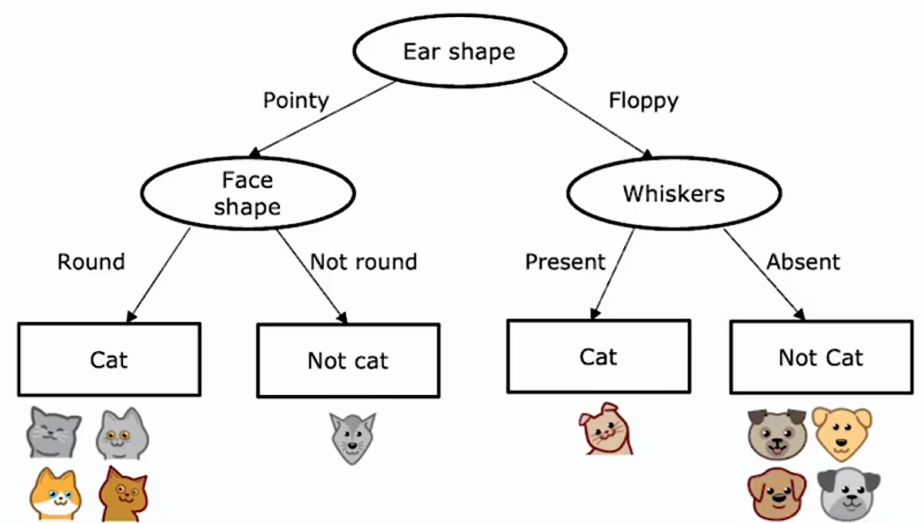
关键决策：

1. 在每个节点如何选择用于划分的特征？以尽量提高纯度
   • 纯度：想得到什么样的子集，这些子集要尽可能全是猫或全不是猫
2. 何时停止分裂？
   1. 我们刚才使用的标准是直到一个节点 100% 是一类（全是猫或全不是猫）
   2. 拆分节点会导致树超过最大深度（超参数）时停止
      • 限制决策树深度的原因是：
      • 首先：要保证树不会变得过于庞大而难以处理
      • 其次：保持树较小，可以减少过拟合的风险
   3. 纯度分数提升低于某个阈值时（熵的减少低于某个阈值）停止
   4. 节点处的样本数量低于某个阈值时停止

纯度

把 $p_1$ 定义为猫（label=1）在所有样本中所占的比例

用一个叫做熵的函数 $H(p_1)$ 来衡量一组样本的不纯程度

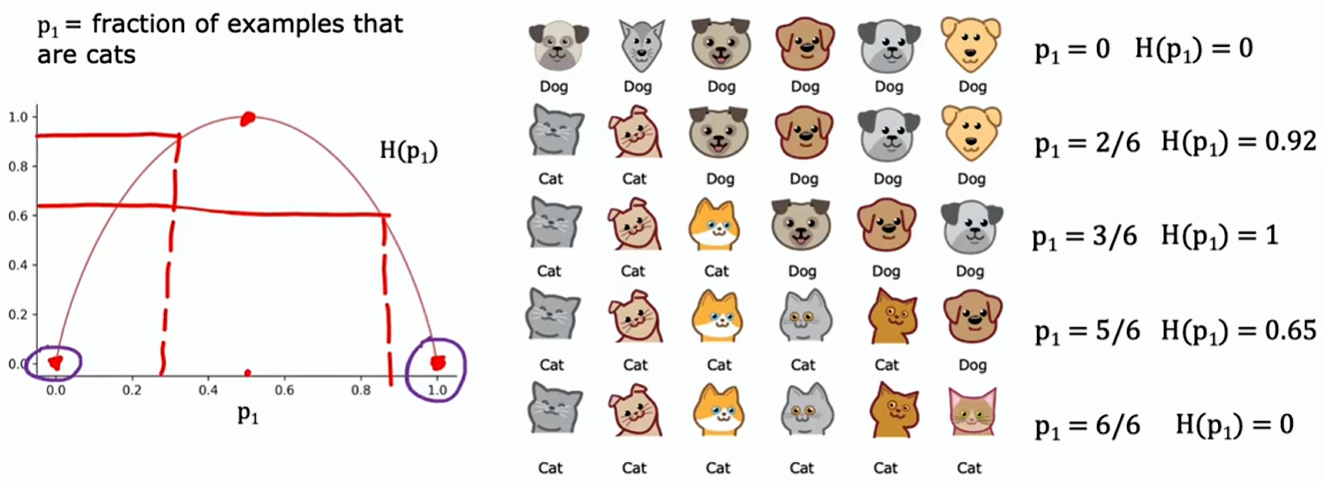
不是猫在所有样本中所占的比例：$p_0=1-p_1$

熵函数：

$$\begin{array}{rl}H(p_1)& =-p_{1}lo{g}_2(p_1)-p_{0}lo{g}_2(p_0)\\ & =-p_{1}lo{g}_2(p_1)-(1-p_1)lo{g}_2(1-p_1)\end{array}$$

取以 2 为底的对数是为了让这条曲线的峰值等于 1；要是取以 $e$ 为底的对数，只是对该函数进行垂直缩放，它依然有效，旦数字会变得有点难以理解，因为函数的峰值不再是一个像 1 这样的整数了

计算此函数时需注意：如果 $p_1$ 或 $p_0$ 等于 0，那么像 $0log(0)$ 这样的表达式就会出现，而 $0log(0)$ 在技术上是未定义的，实际上是负无穷。按照惯例，在计算熵时视作 $0log(0)=0$

你可能还会听说一种叫做基尼系数（Gini criteria）的东西，它是另一种与熵函数非常相似的函数，并且它在构建决策树时也能很好地发挥作用，这里不做展开

信息增益

构建决策树时，我们决定在节点上依据什么特征进行分裂，能最大程度降低熵（减少杂质、最大化纯度）

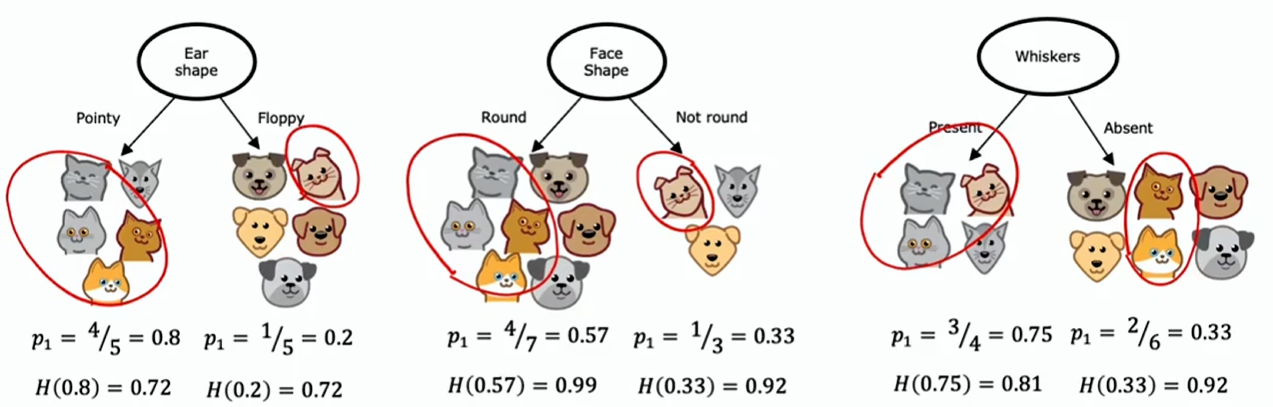
如上图所示，鉴于根节点使用的特征有这三个选项，哪个效果最佳？

事实证明，与其查看这些熵值并比较，对它们进行加权平均会更有用。如果一个节点中有很多例子且熵值很高，这比只有少数例子且熵值很高的节点更糟糕

我们选择分割的方式是计算加权平均，然后选取其中最小的那个

在构建决策树时，实际上要对这些公式再做一次改动，以遵循决策树构建的惯例，但实际上不会改变结果

与其计算这个加权平均熵，不如计算与完全不分割相比的熵减少量

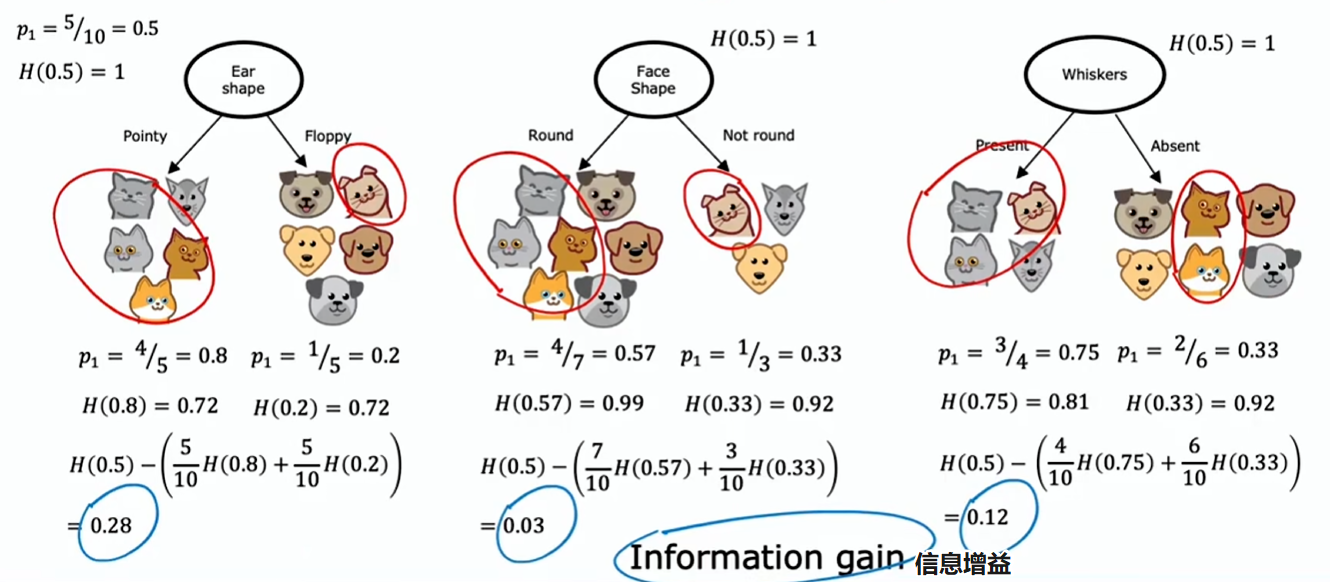
信息增益：衡量的是由于进行分割而在树中获得的熵的减少量

这个例子中：熵最初在根节点处为 1，通过进行分割最终得到了一个较低的值，这两个值之间的差异就是熵的减少量，而在耳形分割的情况下，这个减少量最大，为 0.28

为什么要费心计算熵的减少，而不是仅仅计算左右子分支的熵？

因为决定何时不再进一步分裂的停止标准之一是熵的减少是否太小

计算信息增益的通用公式：

$$Informationgain=H(p_1^{root})-(w^{left}H(p_1^{left})+w^{right}H(p_1^{right}))$$

• $p_1^{left}$：左子树的所有示例中属于正例（label=1）的比例
• $w^{left}$：根节点所有示例中进入左子树的示例所占比例

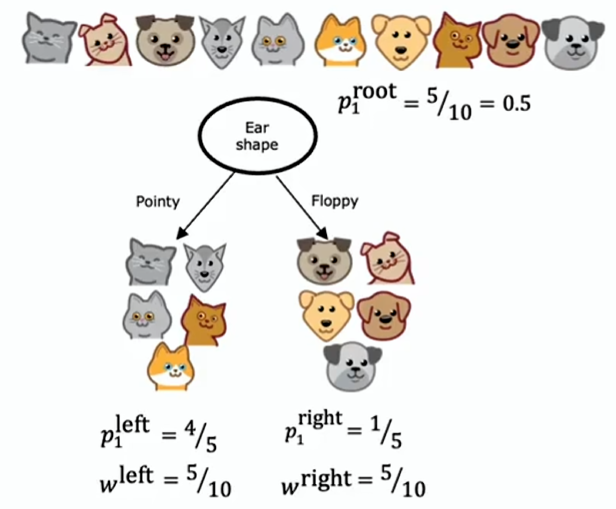
信息增益准则助您决定在单个节点处如何挑选一个特征来进行分割

学习过程回顾

构建决策树的整体过程：

1. 从树的根节点处的所有训练样本开始
2. 计算所有可能特征的信息增益，挑选具有最高信息增益的特征用于分割
3. 选择此特征后，根据所选特征将数据集分为两个子集，创建树的左右分支，并将训练示例发送至左分支或右分支
4. 不断重复拆分过程，直到满足停止条件：（满足这些标准中的一条或多条）
   • 当一个节点完全属于单一类别时
   • 当进一步拆分节点会使树超过你设定的最大深度时
   • 当额外拆分所带来的信息增益小于某个阈值时
   • 当节点中的样本数量低于某个阈值时

多离散值特征

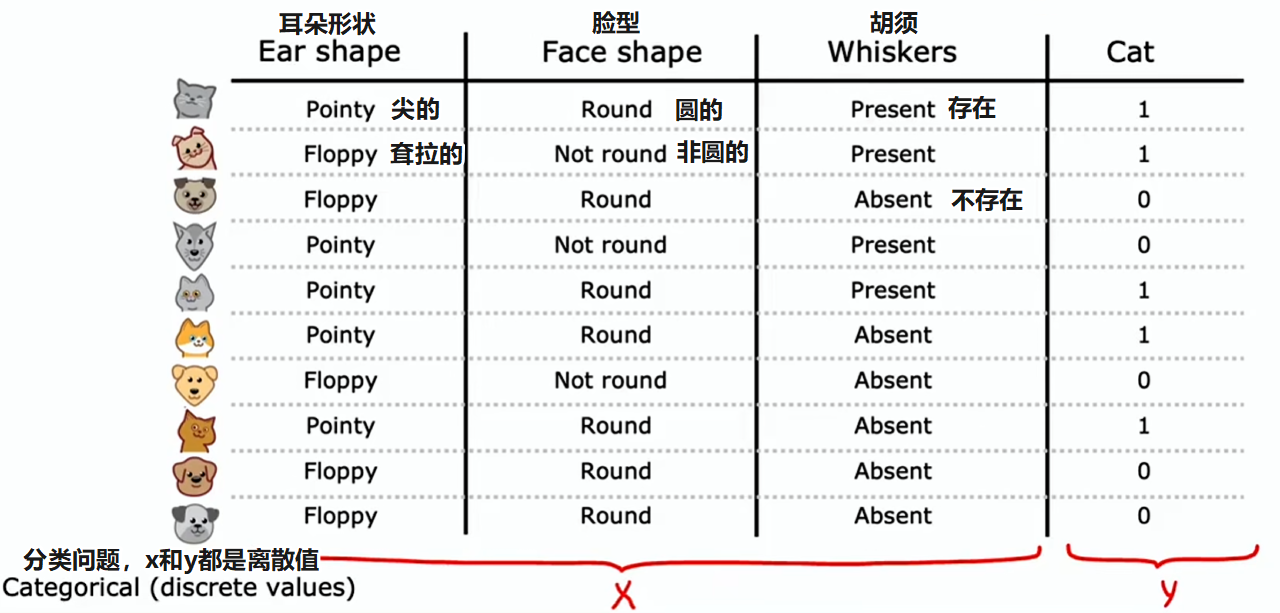
到目前为止我们看到的示例中，每个特征都只能取两个可能值中的一个：耳朵形状不是尖的就是耷拉的、脸型要么是圆的要么不是、胡须要么有要么没有，但要是特征能取两个以上离散值呢？

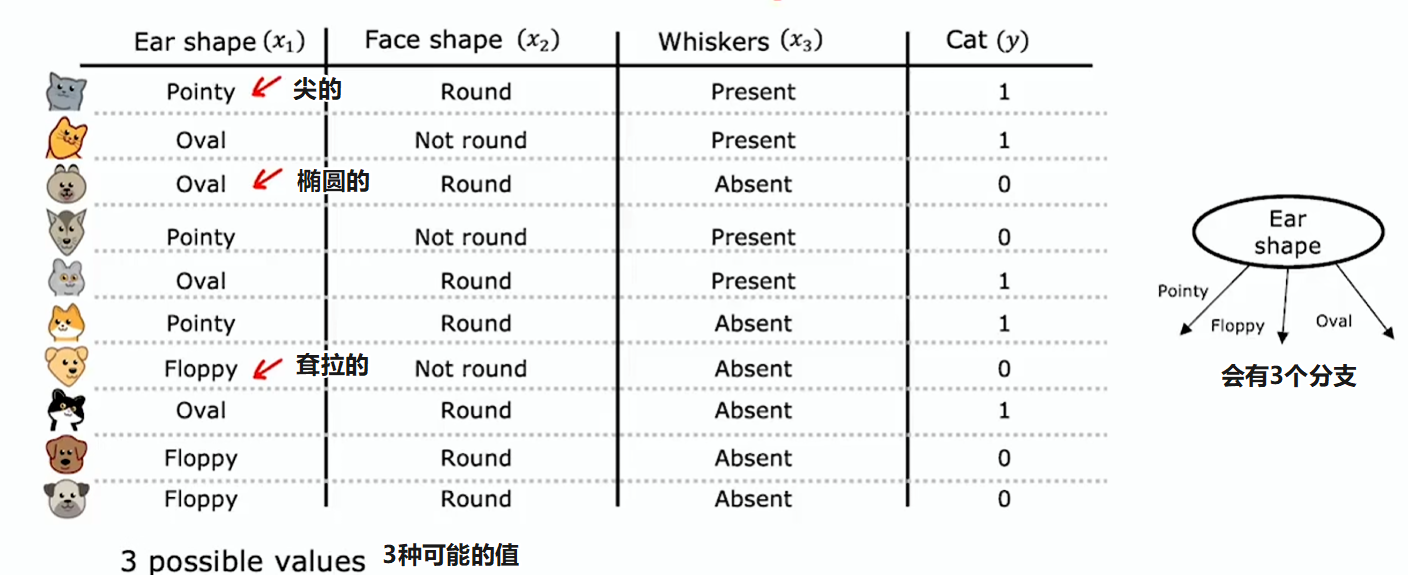
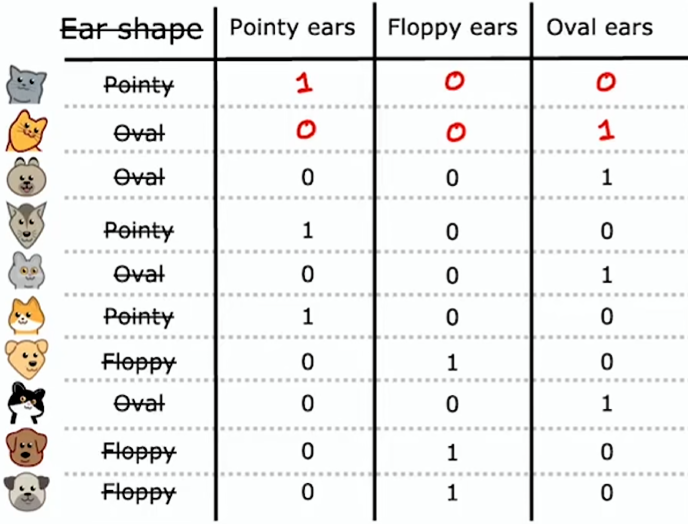
新的方式：不是一个特征有三种取值，而是构建三个新特征，每个新特征只能取 0 或 1

独热编码（Onee hot encoding）：如果一个分类特征有 k 种可能取值，那就通过创建 k 个二进制（只能取 0 或 1）特征来替换它。每个样本的这 k 个二进制特征只会有一个为 1，其他为 0

连续值特征

如何对决策树进行修改，以处理不仅是离散值，而是连续值的特征

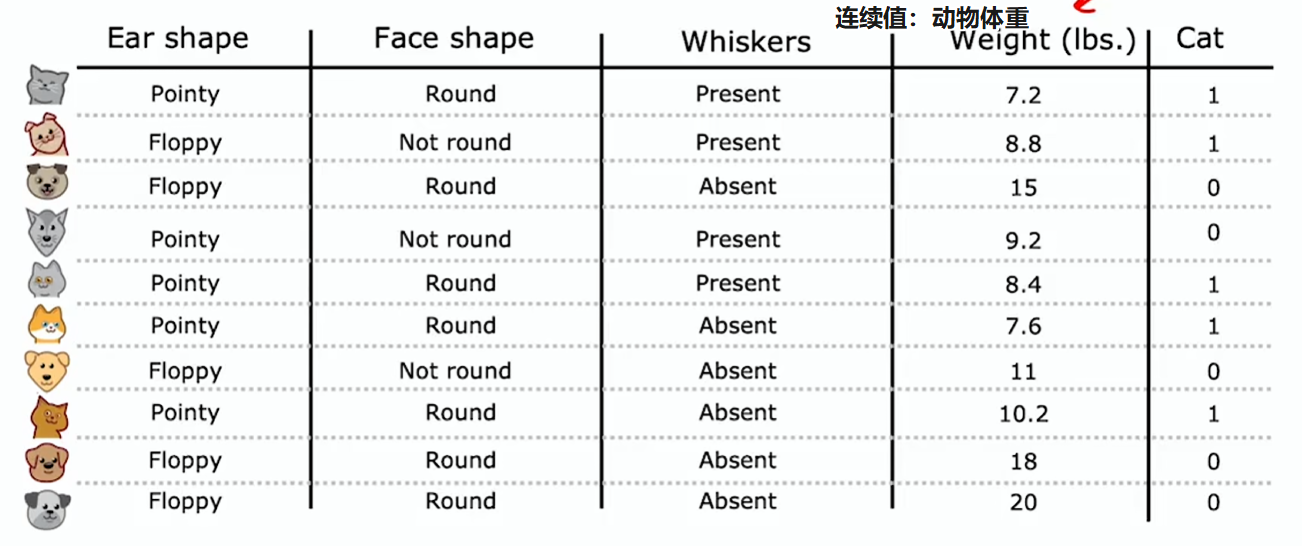
按体重（连续值）特征划分的方式是，根据体重是否小于或等于某个阈值，假设是 8 或其他数字（由学习算法选择）。要考虑该阈值的多个不同值，然后挑选出最佳（信息增益最大）的那个

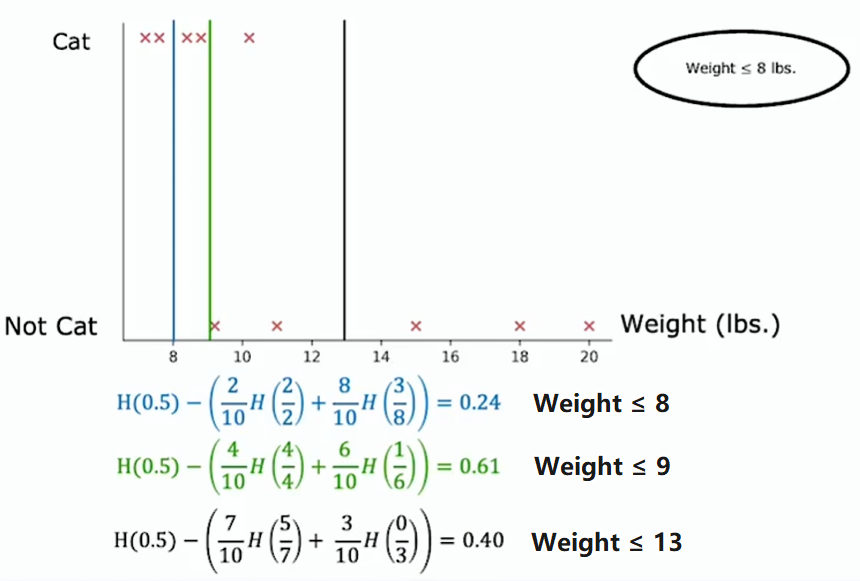
实际上不只是尝试三个值，而是会沿 x 轴尝试多个值

一种做法是根据权重或此特征的值对所有示例进行排序，并取排序后的训练列表中所有中间点的值，作为阈值的候选值