058.区间dp-上

前置知识：讲解067、讲解068 二维动态规划及其空间压缩技巧

区间 dp §

区间 dp：大范围的问题拆分成若干小范围的问题来求解

可能性展开的常见方式：

1. 基于两侧端点讨论的可能性展开
   • 题目1 ~ 题目2
2. 基于范围上划分点的可能性展开
   • 题目3 ~ 题目6
   • 时间复杂度：$O(n^3)$
     • $O(n^2)$：动态规划表的大小
     • $O(n)$：每个格子的枚举代价
   • 空间复杂度：$O(n^2)$
     • 每个格子依赖很多位置格子，所以不能用滚动数组进行空间压缩

区间 dp 专题分为上、下两期，一共 12 个题

本节课会安排 6 个题，熟悉区间 dp 的可能性展开

题目1.让字符串成为回文串的最少插入次数 §

题目描述 §

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

「回文串」是正读和反读都相同的字符串。

示例 1：

输入：s = "zzazz"

输出：0

解释：字符串 "zzazz" 已经是回文串了，所以不需要做任何插入操作。

示例 2：

输入：s = "mbadm"

输出：2

解释：字符串可变为 "mbdadbm" 或者 "mdbabdm"。

提示：

• 1 <= s.length <= 500
• s 中所有字符都是小写字母。

测试链接 §

1312.让字符串成为回文串的最少插入次数

思路 §

本题和 最长回文子序列 的区间 dp 解法高度相似

暴力递归 §

var (
	S string
)
 
func minInsertions(s string) int {
	S = s
	return f(0, len(s)-1)
}
 
// s[l:r+1] 这个范围上的字符串，整体都变成回文串
// 返回至少插入几个字符
func f(l, r int) int {
	if l == r {
		// 就一个字符，已经是回文串了
		return 0
	} else if l+1 == r {
		// 两个字符
		if S[l] == S[r] {
			// 两个字符相同，已经是回文串了
			return 0
		} else {
			// 两个字符不同，插入一个字符就能变成回文串
			return 1
		}
	} else if S[l] == S[r] {
		// 两边字符相同，只需要管中间的字符串
		return f(l+1, r-1)
	} else {
		// 两边字符不同，在左边或右边插入一个字符来搞定右边或左边的已有字符
		return min(f(l+1, r), f(l, r-1)) + 1
	}
}

记忆化搜索 §

l、r 的范围在 $[0,n-1]$

var (
	S     string
	cache [][]int
)
 
func minInsertions(s string) int {
	S = s
	n := len(s)
	cache = make([][]int, n)
	for i := range cache {
		cache[i] = make([]int, n)
		for j := range cache[i] {
			cache[i][j] = -1
		}
	}
	return f(0, n-1)
}
 
// s[l:r+1] 这个范围上的字符串，整体都变成回文串
// 返回至少插入几个字符
func f(l, r int) int {
	if cache[l][r] != -1 {
		return cache[l][r]
	}
	ans := 0
	if l == r {
		// 就一个字符，已经是回文串了
		ans = 0
	} else if l+1 == r {
		// 两个字符
		if S[l] == S[r] {
			// 两个字符相同，已经是回文串了
			ans = 0
		} else {
			// 两个字符不同，插入一个字符就能变成回文串
			ans = 1
		}
	} else if S[l] == S[r] {
		// 两边字符相同，只需要管中间的字符串
		ans = f(l+1, r-1)
	} else {
		// 两边字符不同，在左边或右边插入一个字符来搞定右边或左边的已有字符
		ans = min(f(l+1, r), f(l, r-1)) + 1
	}
 
	cache[l][r] = ans
	return ans
}

严格位置依赖的动态规划 §

func minInsertions(s string) int {
	n := len(s)
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, n)
	}
 
	// 初始化：对角线 = 0，l+1=r 位置 = 0/1
	for l := 0; l < n-1; l++ {
		if s[l] != s[l+1] {
			dp[l][l+1] = 1
		}
	}
 
	// 从下往上，从左往右递推
	for l := n - 3; l >= 0; l-- {
		for r := l + 2; r < n; r++ {
			if s[l] == s[r] {
				dp[l][r] = dp[l+1][r-1]
			} else {
				dp[l][r] = min(dp[l+1][r], dp[l][r-1]) + 1
			}
		}
	}
 
	return dp[0][n-1]
}

空间压缩 §

func minInsertions(s string) int {
	n := len(s)
	dp := make([]int, n)
	leftBottom, backup := 0, 0
	// 从下往上，从左往右递推
	for l := n - 2; l >= 0; l-- {
		// 初始化：l+1 == r 线
		if l+1 < n {
			leftBottom = dp[l+1]
			if s[l] != s[l+1] {
				dp[l+1] = 1
			}
		}
		// 普通位置
		for r := l + 2; r < n; r++ {
			backup = dp[r]
			if s[l] == s[r] {
				dp[r] = leftBottom
			} else {
				dp[r] = min(dp[r], dp[r-1]) + 1
			}
			leftBottom = backup
		}
	}
 
	return dp[n-1]
}

题目2.预测赢家 §

题目描述 §

给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是 0 。每一回合，玩家从数组的任意一端取一个数字（即，nums[0] 或 nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减 1）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

如果玩家 1 能成为赢家，返回 true 。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 10^7

测试链接 §

486.预测赢家

暴力递归 §

var (
	theNums []int
)
 
func predictTheWinner(nums []int) bool {
	n := len(nums)
	theNums = nums
	first := f(0, n-1)
	sum := 0
	for _, num := range nums {
		sum += num
	}
	second := sum - first
	return first >= second
}
 
// nums[l:r+1] 范围上的数字进行游戏，轮到玩家 1
// 返回玩家 1 最终能获得多少分数
// 玩家 1 和玩家 2 都绝顶聪明，nums 元素都非负
func f(l, r int) int {
	if l == r {
		// 就剩 1 个数，拿走
		return theNums[l]
	} else if l+1 == r {
		// 剩 2 个数，拿较大的
		return max(theNums[l], theNums[r])
	} else {
		// 不止两个数
		// 可能性 1：玩家 1 拿走 nums[l]，玩家 2 会在 l+1 ~ r 两端做一个对玩家 1 最不利的选择
		p1 := theNums[l] + min(f(l+2, r), f(l+1, r-1))
		// 可能性 2：玩家 1 拿走 nums[r]，玩家 2 会在 l ~ r-1 两端做一个对玩家 1 最不利的选择
		p2 := theNums[r] + min(f(l+1, r-1), f(l, r-2))
		// 玩家 1 在两种可能中做最利于自己的选择
		return max(p1, p2)
	}
}

记忆化搜索 §

var (
	theNums []int
	cache   [][]int
)
 
func predictTheWinner(nums []int) bool {
	n := len(nums)
	theNums = nums
	cache = make([][]int, n)
	for i := range cache {
		cache[i] = make([]int, n)
		for j := range cache[i] {
			cache[i][j] = -1
		}
	}
	first := f(0, n-1)
	sum := 0
	for _, num := range nums {
		sum += num
	}
	second := sum - first
	return first >= second
}
 
// nums[l:r+1] 范围上的数字进行游戏，轮到玩家 1
// 返回玩家 1 最终能获得多少分数
// 玩家 1 和玩家 2 都绝顶聪明，nums 元素都非负
func f(l, r int) int {
	if cache[l][r] != -1 {
		return cache[l][r]
	}
	ans := 0
	if l == r {
		// 就剩 1 个数，拿走
		ans = theNums[l]
	} else if l+1 == r {
		// 剩 2 个数，拿较大的
		ans = max(theNums[l], theNums[r])
	} else {
		// 不止两个数
		// 可能性 1：玩家 1 拿走 nums[l]，玩家 2 会在 l+1 ~ r 两端做一个对玩家 1 最不利的选择
		p1 := theNums[l] + min(f(l+2, r), f(l+1, r-1))
		// 可能性 2：玩家 1 拿走 nums[r]，玩家 2 会在 l ~ r-1 两端做一个对玩家 1 最不利的选择
		p2 := theNums[r] + min(f(l+1, r-1), f(l, r-2))
		// 玩家 1 在两种可能中做最利于自己的选择
		ans = max(p1, p2)
	}
 
	cache[l][r] = ans
	return ans
}

位置依赖 §

每个格子依赖 l+1/2、r-1/2 位置，即：左、下，所以从下往上、从左往右递推

初始化：对角线（l==r）、l+1==r 线

func predictTheWinner(nums []int) bool {
	n := len(nums)
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, n)
		dp[i][i] = nums[i]
		if i+1 < n {
			dp[i][i+1] = max(nums[i], nums[i+1])
		}
	}
	for l := n - 3; l >= 0; l-- {
		for r := l + 2; r < n; r++ {
			dp[l][r] = max(
				nums[l]+min(dp[l+2][r], dp[l+1][r-1]),
				nums[r]+min(dp[l+1][r-1], dp[l][r-2]),
			)
		}
	}
	first := dp[0][n-1]
	sum := 0
	for _, num := range nums {
		sum += num
	}
	second := sum - first
	return first >= second
}

空间压缩 §

因为每一行依赖下一行（l+1）和下下一行（l+2），就不能用一个数组进行滚动了，应该用两个数组轮替滚动

代码略

题目3.多边形三角剖分的最低得分 §

题目描述 §

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

示例 1：

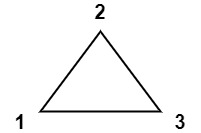
输入：values = [1,2,3]

输出：6

解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

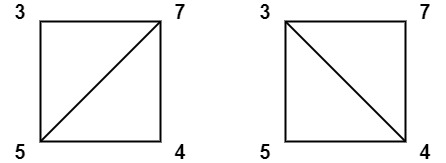
输入：values = [3,7,4,5]

输出：144

解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

提示：

• n == values.length
• 3 <= n <= 50
• 1 <= values[i] <= 100

测试链接 §

1039.多边形三角剖分的最低得分

思路 §

划分三角形：$[l,r]$ 的点，遍历 $(l,r)$ 为划分点 m，l、r、m 三点为一个三角形，在 $[l,m]$ 和 $[m,r]$ 继续划分下去，这样不会有 $[l,m]$ 和 $[m,r]$ 上的点连接（即：交叉三角形）的情况出现

记忆化搜索 §

var (
	theValues []int
	cache     [][]int
)
 
func minScoreTriangulation(values []int) int {
	n := len(values)
	theValues = values
	cache = make([][]int, n)
	for i := range cache {
		cache[i] = make([]int, n)
		for j := range cache[i] {
			cache[i][j] = -1
		}
	}
	return f(0, n-1)
}
 
// values[l:r+1] 范围中求解
func f(l, r int) int {
	if cache[l][r] != -1 {
		return cache[l][r]
	}
	ans := math.MaxInt
	if r-l < 2 {
		// 构不成三角形
		ans = 0
	} else {
		for m := l + 1; m < r; m++ {
			// 以 m 做划分点
			// l、r、m 三点构成一个三角形
			// 在 l~m 和 m~r 继续划分
			ans = min(ans, f(l, m)+theValues[l]*theValues[m]*theValues[r]+f(m, r))
		}
	}
 
	cache[l][r] = ans
	return ans
}

位置依赖 §

每个格子依赖左、下位置，所以从下往上、从左往右递推

func minScoreTriangulation(values []int) int {
	n := len(values)
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, n)
	}
	for l := n - 3; l >= 0; l-- {
		for r := l + 2; r < n; r++ {
			dp[l][r] = math.MaxInt
			for m := l + 1; m < r; m++ {
				dp[l][r] = min(dp[l][r], dp[l][m]+values[l]*values[m]*values[r]+dp[m][r])
			}
		}
	}
	return dp[0][n-1]
}

题目4.切棍子的最小成本 §

题目描述 §

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

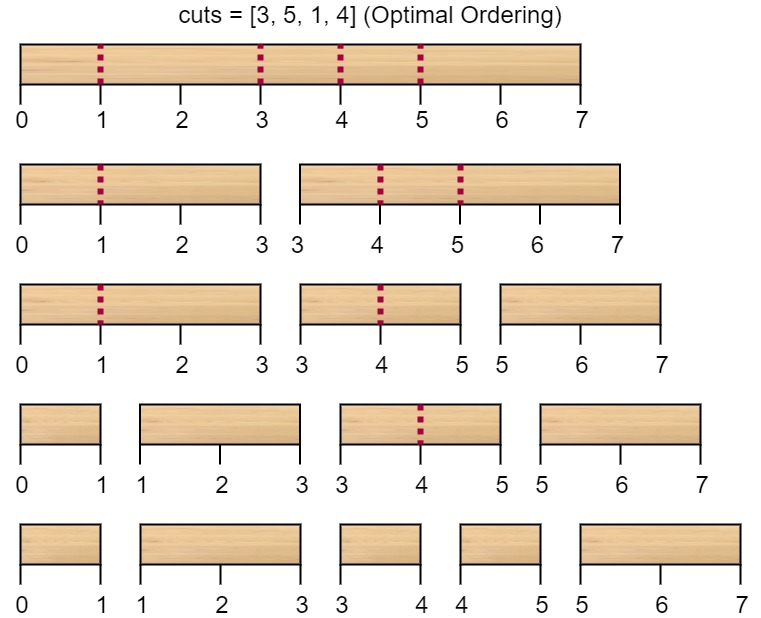
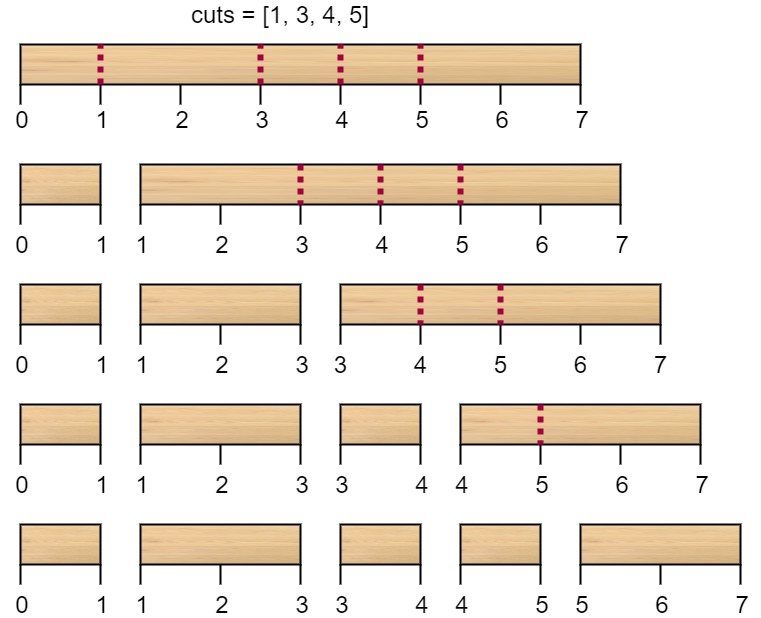
输入：n = 7, cuts = [1,3,4,5]

输出：16

解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

第一次切割长度为 7 的棍子，成本为 7。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20。

而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]

输出：22

解释：如果按给定的顺序切割，则总成本为 25。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

• 2 <= n <= 10^6
• 1 <= cuts.length <= min(n - 1, 100)
• 1 <= cuts[i] <= n - 1
• cuts 数组中的所有整数都 互不相同

测试链接 §

1547.切棍子的最小成本

思路 §

如何确定切一个点的时候它的代价是多少？

需要数据预处理：cuts 排序后，前面加个 0，后面加个 n

如：示例 1 n = 7, cuts = [1,3,4,5]，预处理后 arr=[0,1,3,4,5,7]

在 l=1, r=4 选一个点切第一刀，它的代价就是 arr[r+1] - arr[l-1]

记忆化搜索 §

var (
	arr   []int
	cache [][]int
)
 
func minCost(n int, cuts []int) int {
	m := len(cuts)
	sort.Ints(cuts)
	arr = make([]int, m+2)
	arr[0] = 0
	copy(arr[1:m+1], cuts)
	arr[m+1] = n
	cache = make([][]int, m+2)
	for i := range cache {
		cache[i] = make([]int, m+2)
		for j := range cache[i] {
			cache[i][j] = -1
		}
	}
	return f(1, m)
}
 
// 切点 [l, r]，决定一个顺序
// 让切点都切完，总代价最小
func f(l, r int) int {
	if l > r {
		return 0
	}
	if cache[l][r] != -1 {
		return cache[l][r]
	}
	ans := math.MaxInt
	// 遍历切点找子过程最小代价
	for k := l; k <= r; k++ {
		ans = min(ans, f(l, k-1)+f(k+1, r))
	}
	// k 切点的代价
	ans += arr[r+1] - arr[l-1]
 
	cache[l][r] = ans
	return ans
}

位置依赖 §

每个格子依赖左、下位置，所以从下往上、从左往右递推

初始化：l == r 时，切割点只有一个

func minCost(n int, cuts []int) int {
	m := len(cuts)
	sort.Ints(cuts)
	arr := make([]int, m+2)
	arr[0] = 0
	copy(arr[1:m+1], cuts)
	arr[m+1] = n
	dp := make([][]int, m+2)
	for i := range dp {
		dp[i] = make([]int, m+2)
 
	}
 
	// 初始化：l == r 时，切割点只有一个
	for i := 1; i <= m; i++ {
		dp[i][i] = arr[i+1] - arr[i-1]
	}
 
	for l := m - 1; l >= 1; l-- {
		for r := l + 1; r <= m; r++ {
			next := math.MaxInt
			for k := l; k <= r; k++ {
				next = min(next, dp[l][k-1]+dp[k+1][r])
			}
			dp[l][r] = arr[r+1] - arr[l-1] + next
		}
	}
 
	return dp[1][m]
}

题目5.戳气球 §

题目描述 §

有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

求所能获得硬币的最大数量。

示例 1：

输入：nums = [3,1,5,8]

输出：167

解释：

nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []

coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167

示例 2：

输入：nums = [1,5]

输出：10

提示：

• n == nums.length
• 1 <= n <= 300
• 0 <= nums[i] <= 100

测试链接 §

312.戳气球

思路 §

如何确定打爆某个气球，它相邻的左右两个未爆的气球是哪个？

递归函数保证：[l,r] 中 l-1 和 r+1 一定没爆，尝试每个气球最后打爆

因为 [l,r] 中 l-1 和 r+1 一定没爆，某个气球最后爆（即：[l,r] 其他气球都已经爆了），那么这个气球的相邻的左右两个未爆的气球就是 l-1 和 r+1

数据预处理：最左和最右个加一个 1，避免很多边界讨论

记忆化搜索 §

var (
	arr   []int
	cache [][]int
)
 
func maxCoins(nums []int) int {
	n := len(nums)
	arr = make([]int, n+2)
	arr[0] = 1
	arr[n+1] = 1
	copy(arr[1:n+1], nums)
	cache = make([][]int, n+2)
	for i := range cache {
		cache[i] = make([]int, n+2)
		for j := range cache[i] {
			cache[i][j] = -1
		}
	}
	return f(1, n)
}
 
// arr[l:r+1] 这些气球决定一个顺序，获得最大得分返回
// 保证 l-1 和 r+1 气球一定没爆
func f(l, r int) int {
	if cache[l][r] != -1 {
		return cache[l][r]
	}
	ans := 0
	if l == r {
		// 只有一个气球
		ans = arr[l-1] * arr[l] * arr[r+1]
	} else {
		// 尝试每个气球最后打爆
		for k := l; k <= r; k++ {
			ans = max(ans, arr[l-1]*arr[k]*arr[r+1]+f(l, k-1)+f(k+1, r))
		}
	}
	cache[l][r] = ans
	return ans
}

位置依赖 §

每个格子依赖左、下位置，所以从下往上、从左往右递推

初始化：l == r 时，只有一个气球

func maxCoins(nums []int) int {
	n := len(nums)
	arr := make([]int, n+2)
	arr[0] = 1
	arr[n+1] = 1
	copy(arr[1:n+1], nums)
	dp := make([][]int, n+2)
	for i := range dp {
		dp[i] = make([]int, n+2)
	}
	for i := 1; i <= n; i++ {
		// 初始化：只有一个气球
		dp[i][i] = arr[i-1] * arr[i] * arr[i+1]
	}
	for l := n; l >= 1; l-- {
		for r := l + 1; r <= n; r++ {
			for k := l; k <= r; k++ {
				dp[l][r] = max(dp[l][r], arr[l-1]*arr[k]*arr[r+1]+dp[l][k-1]+dp[k+1][r])
			}
		}
	}
	return dp[1][n]
}

题目6.布尔运算 §

题目描述 §

给定一个布尔表达式和一个期望的布尔结果 result，布尔表达式由以下符号组成：

• 0：false
• 1：true
• &：AND
• |：OR
• ^：XOR

布尔表达式一定是正确的，不需要检查有效性

但是其中没有任何括号来表示优先级，你可以随意添加括号来改变逻辑优先级，目的是让表达式能够最终得出 result 的结果

返回最终得出 result 有多少种不同的逻辑计算顺序

示例 1：

输入：s = "1^0|0|1", result = 0

输出：2

解释：两种可能的括号方法是：1^(0|(0|1))、1^((0|0)|1)

示例 2：

输入：s = "0&0&0&1^1|0", result = 1

输出：10

提示：

• 运算符的数量不超过 19 个

测试链接 §

面试题 08.14.布尔运算

思路 §

题目保证了 s 这个布尔表达式一定是合法的，所以：

• len(s) 一定是奇数
• 偶数索引一定是布尔值：0、1
• 奇数索引一定是运算符：&、|、^

记忆化搜索 §

var (
	S     string
	cache [][][]int
)
 
func countEval(s string, result int) int {
	S = s
	n := len(s)
	cache = make([][][]int, n)
	for i := range cache {
		cache[i] = make([][]int, n)
	}
	return process(0, n-1)[result]
}
 
// s[l:r+1] 是表达式的一部分，且一定符合范式
// 返回：[0 的计算逻辑数, 1 的计算逻辑数]
func process(l, r int) []int {
	if cache[l][r] != nil {
		return cache[l][r]
	}
	f, t := 0, 0
	if l == r {
		// 只剩一个字符：0 或 1
		if S[l] == '0' {
			f = 1
			t = 0
		} else {
			f = 0
			t = 1
		}
	} else {
		// 枚举每一个逻辑符号最后执行
		var tmp []int
		var a, b, c, d int
		for k := l + 1; k < r; k += 2 {
			tmp = process(l, k-1)
			a = tmp[0]
			b = tmp[1]
			tmp = process(k+1, r)
			c = tmp[0]
			d = tmp[1]
			if S[k] == '&' {
				f += a*c + a*d + b*c
				t += b * d
			} else if S[k] == '|' {
				f += a * c
				t += a*d + b*c + b*d
			} else if S[k] == '^' {
				f += a*c + b*d
				t += a*d + b*c
			}
		}
	}
 
	cache[l][r] = []int{f, t}
	return cache[l][r]
}

位置依赖 §

func countEval(s string, result int) int {
	n := len(s)
	dp := make([][][2]int, n)
	for i := range dp {
		dp[i] = make([][2]int, n)
		// 初始化：l == r
		if s[i] == '0' {
			dp[i][i][0] = 1
			dp[i][i][1] = 0
		} else {
			dp[i][i][0] = 0
			dp[i][i][1] = 1
		}
	}
 
	a, b, c, d := 0, 0, 0, 0
	for l := n - 3; l >= 0; l -= 2 {
		for r := l + 2; r < n; r += 2 {
			for k := l + 1; k < r; k += 2 {
				a = dp[l][k-1][0]
				b = dp[l][k-1][1]
				c = dp[k+1][r][0]
				d = dp[k+1][r][1]
				if s[k] == '&' {
					dp[l][r][0] += a*c + a*d + b*c
					dp[l][r][1] += b * d
				} else if s[k] == '|' {
					dp[l][r][0] += a * c
					dp[l][r][1] += a*d + b*c + b*d
				} else if s[k] == '^' {
					dp[l][r][0] += a*c + b*d
					dp[l][r][1] += a*d + b*c
				}
			}
		}
	}
 
	return dp[0][n-1][result]
}