050.见识更多二维动态规划题目

前置知识：从递归入手二维动态规划

本节课不再从递归入手，而是直接从动态规划的定义入手，来见识更多二维动态规划问题

本节课包含一些比较巧妙的尝试思路

备注

题目1.不同的子序列 §

题目描述 §

给你两个字符串 s 和 t，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 10^9+7 取模。

提示：

• 1 <= s.length, t.length <= 1000
• s 和 t 由英文字母组成

测试链接 §

115.不同的子序列

位置依赖 §

func numDistinct(s string, t string) int {
	sLen, tLen := len(s), len(t)
	// dp[i][j]：s[前缀长度为 i] 的所有子序列中，有多少个子序列等于 t[前缀长度为 j]
	dp := make([][]int, sLen+1)
	for i := range dp {
		dp[i] = make([]int, tLen+1)
		dp[i][0] = 1 // t 长度为 0：一个子序列，为空串
		// dp[0][j] = 0
	}
	for i := 1; i <= sLen; i++ {
		for j := 1; j <= tLen; j++ {
			dp[i][j] = dp[i-1][j] // 不要 s[i-1] 的字符
			if s[i-1] == t[j-1] {
			    // 要 s[i-1] 的字符，相等才能要
				dp[i][j] += dp[i-1][j-1] // s[i-1] 位置搞定了，之前位置怎么样？
			}
		}
	}
	return dp[sLen][tLen]
}

空间压缩 §

一个格子依赖上和左上格子

滚动行，从上往下，从右往左填格子

func numDistinct(s string, t string) int {
	sLen, tLen := len(s), len(t)
	dp := make([]int, tLen+1)
	dp[0] = 1
	for i := 1; i <= sLen; i++ {
		for j := tLen; j >= 1; j-- {
			if s[i-1] == t[j-1] {
				dp[j] += dp[j-1]
			}
		}
	}
	return dp[tLen]
}

题目2.编辑距离 §

工程上非常常用的一个算法，非常重要的一个算法，用来评价两个字符串的相似程度

编辑距离

题目描述 §

给你两个单词 word1 和 word2，返回将 word1 转换成 word2 所使用的最少代价

你可以对一个单词进行如下三种操作：

• 插入一个字符，代价 a
• 删除一个字符，代价 b
• 替换一个字符，代价 c

leetcode 这道题是一个阉割版本：a、b、c 都是 1

测试链接 §

72.编辑距离

思路 §

s1[i 个] -> s2[j 个]，也就是：s1[:i] -> s2[:j]

所有变化的可能：

1. s1[i-1] 参与变化
   1. s1[i-1] 变成 s2[j-1]
      1. 如果 s1[i-1] == s2[j-1]，只需要搞定前面的字符就行，即：dp[i-1][j-1]（情况一）
      2. 如果 s1[i-1] != s2[j-1]，需要搞定前面的字符 + s1[i-1] 替换为 s2[j-1]，即：dp[i-1][j-1] + c（情况二）
   2. s1[i-1] 不去变成 s2[j-1]
      1. s1[:i] 去搞定 s2[:j-1]，再在 s1 后面插入一个 s2[j-1] 字符即可，即：dp[i][j-1] + a（情况三）
2. s1[i-1] 不参与变化
   1. s1[i-1] 不参与变化就是删除 s1[i-1]，用 s1[:i-1] 搞定 s2[:j]，即：dp[i-1][j] + b（情况四）

优化：如果 s1[i-1] == s2[j-1] 时，情况一就是最好的答案，不需要再考虑情况二三四了

格子依赖与初始化：

位置依赖 §

func minDistance(word1 string, word2 string) int {
	return editDistance(word1, word2, 1, 1, 1)
}
 
// 编辑距离：s1 变成 s2 的最小代价
// a: s1 中插入一个字符的代价
// b: s1 中删除一个字符的代价
// c: s1 中替换一个字符的代价
func editDistance(s1, s2 string, a, b, c int) int {
	n1, n2 := len(s1), len(s2)
	// dp[i][j]: s1[:i] -> s2[:j] 最小代价
	dp := make([][]int, n1+1)
	for i := range dp {
		dp[i] = make([]int, n2+1)
	}
	for j := 1; j <= n2; j++ {
		dp[0][j] = a * j
	}
	for i := 1; i <= n1; i++ {
		dp[i][0] = b * i
	}
	for i := 1; i <= n1; i++ {
		for j := 1; j <= n2; j++ {
			if s1[i-1] == s2[j-1] {
				dp[i][j] = dp[i-1][j-1]
			} else {
				dp[i][j] = min(
					dp[i-1][j-1]+c, // 替换
					dp[i][j-1]+a,   // 插入
					dp[i-1][j]+b,   // 删除
				)
			}
		}
	}
	return dp[n1][n2]
}

空间压缩 §

和 最长公共子序列这道题 一样，都依赖左、上、左上三个格子

func minDistance(word1 string, word2 string) int {
	return editDistance(word1, word2, 1, 1, 1)
}
 
// 编辑距离：s1 变成 s2 的最小代价
// a: s1 中插入一个字符的代价
// b: s1 中删除一个字符的代价
// c: s1 中替换一个字符的代价
func editDistance(s1, s2 string, a, b, c int) int {
	n1, n2 := len(s1), len(s2)
	// dp[i][j]: s1[:i] -> s2[:j] 最小代价
	dp := make([]int, n2+1)
	for j := 1; j <= n2; j++ {
		dp[j] = a * j
	}
	topLeft, backup := 0, 0
	for i := 1; i <= n1; i++ { // 从上往下
		dp[0] = b * i
		topLeft = b * (i - 1)
		for j := 1; j <= n2; j++ { // 从左往右
			backup = dp[j]
			if s1[i-1] == s2[j-1] {
				dp[j] = topLeft
			} else {
				dp[j] = min(
					topLeft+c, // 替换
					dp[j-1]+a, // 插入
					dp[j]+b,   // 删除
				)
			}
			topLeft = backup
		}
	}
	return dp[n2]
}

复杂度 §

• 时间复杂度：$O(n\ast m)$，其中 $n$ 为 s1 长度，$m$ 为 s2 长度
  • $n\ast m$ 是 dp 表大小
  • 每个格子的枚举是 $O(1)$
• 空间复杂度：$O(n\ast m)$
  • 空间压缩后：$O(m)$

题目3.交错字符串 §

题目描述 §

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

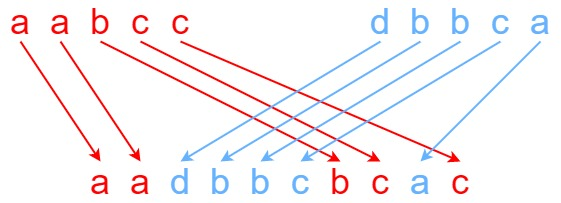
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"

输出：true

提示：

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1、s2、和 s3 都由小写英文字母组成

测试链接 §

97.交错字符串

思路 §

最直接的想法是三指针：三个指针一直往后移，都移出自己的字符串，就是 true

这是不对的，因为相同字符时不知道选择哪个（移动哪个指针）

要用动态规划解

dp[i][j]：s1[:i] 和 s2[:j] 能否交错组成出 s3[:i+j]

为 true 的情况：

1. s1 搞定最后一个字符：s1[i-1] == s3[i+j-1] 并且 dp[i-1][j]
2. s2 搞定最后一个字符：s2[j-1] == s3[i+j-1] 并且 dp[i][j-1]

满足其中之一就是 true

一个格子依赖左和上两个位置

第一行和第一列初始化：s2 或 s1 能否单独搞定 s3

位置依赖 §

func isInterleave(s1 string, s2 string, s3 string) bool {
	n1, n2, n3 := len(s1), len(s2), len(s3)
	if n1+n2 != n3 {
		return false
	}
	// dp[i][j]: s1[:i] 和 s2[:j] 能否交错组成出 s3[:i+j]
	dp := make([][]bool, n1+1)
	for i := range dp {
		dp[i] = make([]bool, n2+1)
	}
	dp[0][0] = true
	for j := 1; j <= n2; j++ {
		if s2[j-1] != s3[j-1] {
			break
		}
		dp[0][j] = true
	}
	for i := 1; i <= n1; i++ {
		if s1[i-1] != s3[i-1] {
			break
		}
		dp[i][0] = true
	}
	for i := 1; i <= n1; i++ {
		for j := 1; j <= n2; j++ {
			dp[i][j] = s1[i-1] == s3[i+j-1] && dp[i-1][j] || s2[j-1] == s3[i+j-1] && dp[i][j-1]
		}
	}
	return dp[n1][n2]
}

空间压缩 §

和 最小路径和这道题 一样，都依赖左、上两个格子

func isInterleave(s1 string, s2 string, s3 string) bool {
	n1, n2, n3 := len(s1), len(s2), len(s3)
	if n1+n2 != n3 {
		return false
	}
	if n1 < n2 {
		n1, n2 = n2, n1
		s1, s2 = s2, s1
	}
	// O(min(n, m))
	dp := make([]bool, n2+1)
	dp[0] = true
	for j := 1; j <= n2; j++ {
		if s2[j-1] != s3[j-1] {
			break
		}
		dp[j] = true
	}
	for i := 1; i <= n1; i++ { // 从上往下
		dp[0] = dp[0] && s1[i-1] == s3[i-1]
		for j := 1; j <= n2; j++ { // 从左往右
			dp[j] = s1[i-1] == s3[i+j-1] && dp[j] || s2[j-1] == s3[i+j-1] && dp[j-1]
		}
	}
	return dp[n2]
}

题目4.有效涂色问题 §

题目描述 §

给定 n、m 两个参数，表示一共有 n 个格子，每个格子可以涂上一种颜色，颜色在 m 种里选

当涂满 n 个格子，并且 m 种颜色都使用了，叫一种有效方法

求一共有多少种有效的涂色方法

数据规模：1 <= n, m <= 5000

结果比较大，请 % 1e9+7 之后返回

测试链接 §

来自大厂面试，无在线测试链接，对数器验证

思路 §

dp[i][j]：前 i 个格子涂满 j 种颜色的方法数

dp[i][j] 怎么求？

1. 情况一：之前就将颜色全涂过了
   • dp[i-1][j]：前 i-1 个格子就涂完了 j 种颜色，第 i 个格子在 j 种颜色中随意涂一个都行
   • 即：dp[i-1][j] * j 种方法数
2. 情况二：还有一种颜色没涂
   • dp[i-1][j-1]：前 i-1 个格子还差一种颜色没涂，第 i 个格子要涂一种新的颜色，新的颜色共 m-(j-1) 种
   • 即：dp[i-1][j-1] * (m-j+1) 种方法数

上面两种情况相加就是 dp[i][j] 的答案

状态依赖：一个格子依赖上、左上两个位置

初始化：

• dp[0][j] 和 dp[i][0] 弃而不用
• dp[i][1]：前 i 个格子填充 1 种颜色，m 种方法数
• dp[1][j]（j > 1）：1 个格子填多种颜色？不可能，0 种方法数

答案 §

package main
 
import (
	"fmt"
	"time"
)
 
const (
	MOD = 1e9 + 7
)
 
// 动态规划
func ways1(n, m int) int {
	// dp[i][j]：前 i 个格子涂满 j 种颜色的方法数
	dp := make([][]int, n+1)
	for i := 1; i <= n; i++ {
		dp[i] = make([]int, m+1)
		dp[i][1] = m
	}
	for i := 2; i <= n; i++ {
		for j := 2; j <= m; j++ {
			// 不开辟新颜色
			dp[i][j] = (dp[i-1][j] * j) % MOD
			// 开辟新颜色
			dp[i][j] = (dp[i][j] + dp[i-1][j-1]*(m-j+1)) % MOD
		}
	}
	return dp[n][m]
}
 
// 空间压缩
func ways2(n, m int) int {
	dp := make([]int, m+1)
	dp[1] = m
	for i := 2; i <= n; i++ {
		dp[1] = m
		for j := m; j >= 2; j-- {
			dp[j] = (dp[j] * j) % MOD
			dp[j] = (dp[j] + dp[j-1]*(m-j+1)) % MOD
		}
	}
	return dp[m]
}
 
// 暴力方法
// 把所有填色的方法暴力枚举
// 然后一个一个验证是否有效
// 这是一个带路径的递归
// 无法改成动态规划
func ways3(n, m int) int {
	path := make([]int, n)
	return f(path, 0, n, m)
}
 
func f(path []int, i, n, m int) int {
	if i == n {
		set := make([]bool, m+1)
		colorCnt := 0
		for _, color := range path {
			if !set[color] {
				set[color] = true
				colorCnt++
			}
		}
		if colorCnt == m {
			return 1
		}
		return 0
	}
 
	ans := 0
	for j := 1; j <= m; j++ {
		path[i] = j
		ans += f(path, i+1, n, m)
	}
	return ans
}
 
func main() {
	// 测试的数据量比较小
	// 那是因为数据量大了，暴力方法过不了
	// 但是这个数据量足够说明正式方法是正确的
	N := 9
	M := 9
	for n := 1; n <= N; n++ {
		for m := 1; m <= M; m++ {
			ans1 := ways1(n, m)
			ans2 := ways2(n, m)
			ans3 := ways3(n, m)
			if ans1 != ans2 || ans1 != ans3 {
				fmt.Printf("%d %d: %d %d %d\n", n, m, ans1, ans2, ans3)
				panic("error")
			}
		}
	}
	fmt.Println("ok")
 
	start := time.Now()
	ways1(5000, 4877)
	elapsed := time.Since(start)
	fmt.Println(elapsed)
}

ok
322.559627ms

题目5.删除至少几个字符可以变成另一个字符串的子串 §

题目描述 §

给定两个字符串 s1 和 s2，返回 s1 至少删除多少字符可以成为 s2 的子串

测试链接 §

来自大厂面试，无在线测试链接，对数器验证

思路 §

dp[i][j]：s1[:i] 至少删掉几个字符可以变成 s2[:j] 的任意后缀

返回：最后一行 dp 表的最小值，含义：s1 变成 s2 不断变长的后缀串，即子串

状态转移：

1. s1[i-1] != s2[j-1]：要删掉 s1 的 i-1 字符，即：1+dp[i-1][j]
2. s1[i-1] == s2[j-1]：要保留 s1 的 i-1 字符，即：dp[i-1][j-1]

状态依赖：一个格子依赖上、左上两个位置

初始化：

• dp[0][j]：表示 s1 空串，删掉 0 个字符变成后缀串 ""
• dp[i][0]：表示 s2 空串，删掉 i 个字符变成后缀串 ""

答案 §

package main
 
import (
	"fmt"
	"math/rand"
	"sort"
	"strings"
)
 
// 动态规划
func minDelete1(s1, s2 string) int {
	n1, n2 := len(s1), len(s2)
	// dp[i][j]：s1[:i] 至少删掉几个字符可以变成 s2[:j] 的任意后缀
	dp := make([][]int, n1+1)
	for i := range dp {
		dp[i] = make([]int, n2+1)
		dp[i][0] = i
	}
	for i := 1; i <= n1; i++ {
		for j := 1; j <= n2; j++ {
			if s1[i-1] == s2[j-1] {
				dp[i][j] = dp[i-1][j-1]
			} else {
				dp[i][j] = 1 + dp[i-1][j]
			}
		}
	}
	ans := dp[n1][0]
	for j := 1; j <= n2; j++ {
		ans = min(ans, dp[n1][j])
	}
	return ans
}
 
// 暴力方法
func minDelete2(s1, s2 string) int {
	n1 := len(s1)
	list := []string{}
 
	f(s1, 0, &[]byte{}, &list)
	// 从长到短排序
	sort.Slice(list, func(i, j int) bool {
		return len(list[i]) > len(list[j])
	})
	for _, str := range list {
		// 排序过的，发现子串了，就是答案
		if strings.Contains(s2, str) {
			return n1 - len(str)
		}
	}
	return n1
}
 
// 生成 s1 字符串的所有子序列串
func f(s1 string, i int, path *[]byte, list *[]string) {
	if i == len(s1) {
		*list = append(*list, string(*path))
	} else {
		// 不用 s1[i]
		f(s1, i+1, path, list)
		// 用 s1[i]
		*path = append(*path, s1[i])
		f(s1, i+1, path, list)
		*path = (*path)[:len(*path)-1]
	}
}
 
func main() {
	// 测试的数据量比较小
	// 那是因为数据量大了，暴力方法过不了
	// 但是这个数据量足够说明正式方法是正确的
	n := 12
	v := 3
	testTime := 20000
	for i := 0; i < testTime; i++ {
		n1 := rand.Intn(n) + 1
		n2 := rand.Intn(n) + 1
		s1 := randomString(n1, v)
		s2 := randomString(n2, v)
		ans1 := minDelete1(s1, s2)
		ans2 := minDelete2(s1, s2)
		if ans1 != ans2 {
			fmt.Printf("%s, %s: %d %d\n", s1, s2, ans1, ans2)
			panic("error")
		}
	}
	fmt.Println("ok")
}
 
// 生成长度为 n，有 v 种字符的随机字符串
func randomString(n, v int) string {
	res := make([]byte, n)
	for i := 0; i < n; i++ {
		res[i] = 'a' + byte(rand.Intn(v))
	}
	return string(res)
}