003.绘制和变换三角形

绘制多个点

构成三维模型的基本单位是三角形

WebGL 只能绘制三种图形：

• 点
• 线段
• 三角形

不管三维模型的形状多么复杂，其基本组成部分都是这三种图形

缓冲区对象

之前使用 gl.vertexAttrib3f 等方法向着色器传递数据，它们每次只能传递一个点的数据

WebGL 提供了一种很方便的机制：缓冲区对象（buffer object），它可以一次性地向着色器传入多个顶点的数据。缓冲区对象是 WebGL 系统中的一块内存区域，可以一次性地向缓冲区对象中填充大量的顶点数据，然后将这些数据保存在其中，供顶点着色器使用

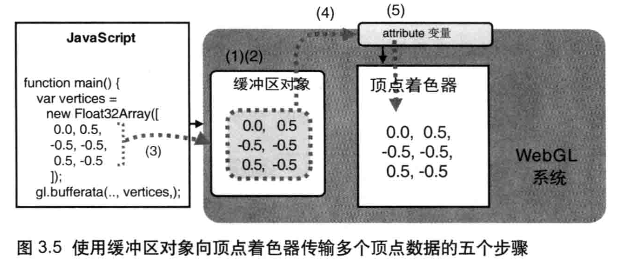
使用缓冲区对象向顶点着色器传入多个顶点的数据，需要遵循以下 5 个步骤：

1. 创建缓冲区对象：gl.createBuffer()
2. 绑定缓冲区对象：gl.bindBuffer()
3. 将数据写入缓冲区对象：gl.bufferData()
4. 将缓冲区对象分配给一个 attribute 变量：gl.vertexAttribPointer()
5. 开启 attribute 变量：gl.enableVertexAttribArray()

处理其他对象，如纹理对象、帧缓冲区对象时的步骤也比较类似

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position; // 声明全局 attribute 变量，数据将从着色器外部传给该变量
void main() {
  gl_Position = a_Position; // 将 attribute 变量赋值 gl_Position
  gl_PointSize = 10.0;
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
 
// 设置顶点位置
const n = initVertexBuffers(gl)
if (n < 0) {
  console.error('设置顶点位置失败')
  return
}
 
// 设置清除颜色并清空 canvas
 
// 绘制图形（三个点）
gl.drawArrays (gl.POINTS, 0, n) // n 是 3
 
/**
 * 创建缓冲区对象，并将多个顶点的数据保存在缓冲区中，然后将缓冲区传给顶点着色器
 */
function initVertexBuffers(gl) {
  // 点的个数
  const n = 3
  // 三个点的坐标信息
  const vertices = new Float32Array([
    0.0, 0.5, -0.5, -0.5, 0.5, -0.5
  ])
 
  // 创建缓冲区对象
  const vertexBuffer = gl.createBuffer()
  if (!vertexBuffer) {
    console.log('创建缓冲区对象失败')
    return -1
  }
 
  // 将缓冲区对象绑定到目标
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
 
  // 向缓冲区对象中写入数据
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
 
  // 获取 attribute 变量的存储位置
  const a_Position = gl.getAttribLocation(gl.program, 'a_Position')
  if (a_Position < 0) {
    console.error(`attribute 变量 'a_Position' 位置获取失败`)
    return -1
  }
 
  // 将缓冲区对象分配给 a_Position 变量
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
 
  // 开启 a_Position 变量与分配给它的缓冲区对象
  gl.enableVertexAttribArray(a_Position)
 
  return n
}

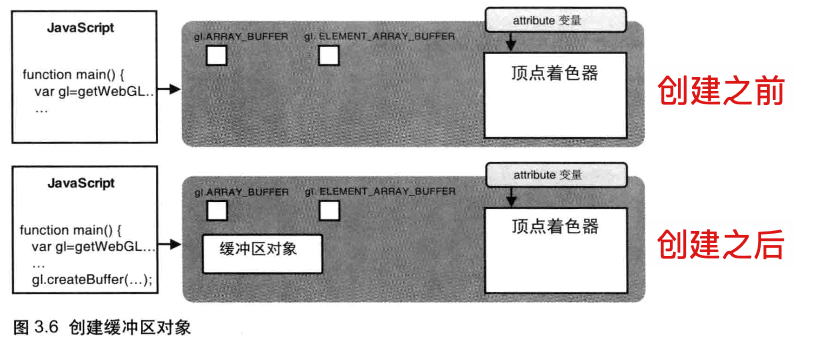
创建缓冲区对象

• gl.createBuffer()：创建缓冲区对象
  • 返回：
    • 非 null：新创建的缓冲区对象
    • null：创建缓冲区对象失败
• gl.deleteBuffer(buffer)：删除参数 buffer 表示的缓冲区对象

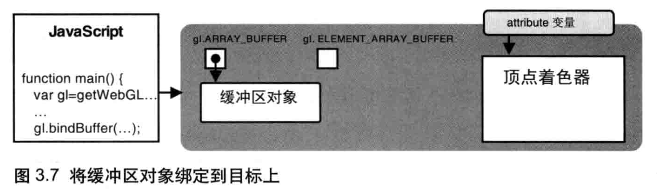
绑定缓冲区对象

将缓冲区对象绑定到 WebGL 系统中已经存在的“目标”， 这个“目标”表示缓冲区对象的用途（这里是向顶点着色器提供传给 attribute 变量的数据），这样 WebGL 才能正确处理其中的内容

gl.bindBuffer(target, buffer)：

• target：目标，可以是以下中的一个：
  • gl.ARRAY_BUFFER：顶点的数据
  • gl.ELEMENT_ARRAY_BUFFER：顶点的索引值
• buffer：之前由 gl.createBuffer() 返回的待绑定的缓冲区对象
  • 如果指定为 null，则禁用对 target 的绑定
• 错误：
  • INVALID_ENUM：target 不是上述值之一，这时将保持原有的绑定情况不变

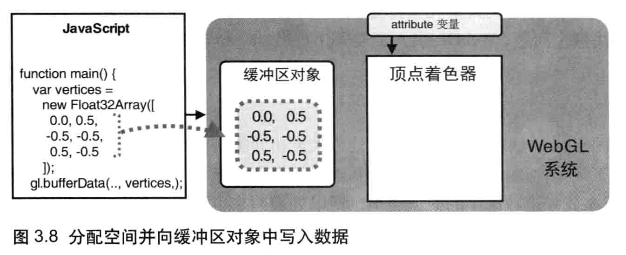
将数据写入缓冲区对象

gl.bufferData(target, data, usage)：开辟存储空间，向绑定在 target 上的缓冲区对象中写入数据 data

• target：gl.ARRAY_BUFFER 或 gl.ELEMENT_ARRAY_BUFFER
• data：数据，类型化数组
• usage：表示程序将如何使用存储在缓冲区对象中的数据。该参数将帮助 WebGL 优化操作，但是就算传入了错误的值，也不会终止程序（仅仅是降低程序的效率）
  • gl.STATIC_DRAW：只会向缓冲区对象中写入一次数据，但需要绘制很多次
  • gl.STREAM_DRAW：只会向缓冲区对象中写入一次数据，然后绘制若干次
  • gl.DYNAMIC_DRAN：会向缓冲区对象中多次写入数据，并绘制很多次
• 错误：
  • INVALID_ENUM：target 不是上述值之一，这时将保持原有的绑定情况不变

该方法的效果是，将 data 写入绑定到 target 上的缓冲区对象。我们不能直接向缓冲区写入数据，而只能向“目标”写入数据，所以要向缓冲区写数据，必须先绑定

将缓冲区对象分配给 attribute 变量

之前，可以使用 gl.vertexAttrib[1234]f() 系列函数为 attribute 变量分配值。但是，这些方法一次只能向 attribute 变量分配（传输）一个值。而现在，需要将整个数组中的所有值一次性地分配给一个 attribute 变量

gl.vertexAttribPointer(location, size, type, normalized, stride, offset)：将绑定到 gl.ARRAY_BUEFER 的缓冲区对象分配给由 location 指定的 attribute 变量

• location：待分配 attribute 变量的存储位置
• size：指定缓冲区中每个顶点的分量个数（1 到 4）
  • 若 size 比 attribute 变量需要的分量数小，缺失的分量将按照与 gl.vertexAttrib[1234]f() 相同的规则 补全
• type：用以下类型之一，指定数据格式：
  • gl.UNSIGNED_BYTE：无符号字节，uint8
  • gl.SHORT：有符号短整型，int16
  • gl.UNSIGNED_SHORT：无符号短整型，uint16
  • gl.INT：有符号整型，int32
  • gl.UNSIGNED_INT：无符号整型，uint32
  • gl.FLOAT：单精度浮点型，float32
• normalized：boolean，是否将非浮点型的数据归一化到 [0, 1] 或 [-1, 1] 区间
• stride：指定相邻两个顶点间的字节数，默认为 0
• offset：指定缓冲区对象中的偏移量（以字节为单位），即 attribute 变量从缓冲区中的何处开始读取或存储数据。如果是从起始位置开始，设为 0
• 错误：
  • INVALID_OPERATION：不存在当前程序对
  • INVALID_VALUE：location 大于等于 attribute 变量的最大数目（默认为 8）。 或者 stride 或 offset 是负值

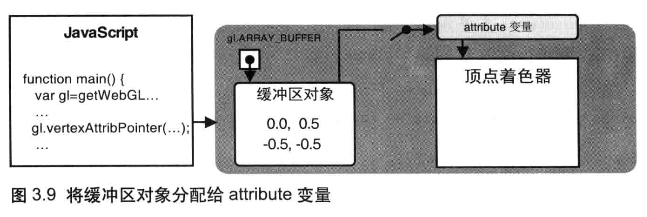
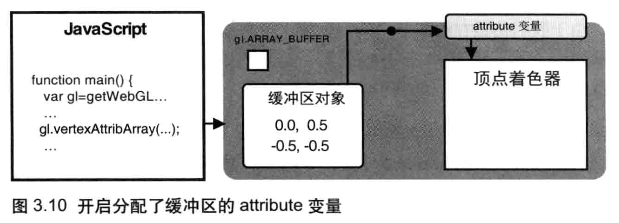
开启 attribute 变量

开启（激活）attribute 变量，使缓冲区对 attribute 变量的分配生效

• gl.enableVertexArray(location)：开启 location 指定的 attribute 变量
  • location：指定 attribue 变量的存储位置
  • 错误：
    • INVALID_VALUE：location 大于等于 attribute 变量的最大数目（默认为 8）
• gl.disableVertexArray(location)：关闭 location 指定的 attribute 变量
  • 参数和错误同 gl.enableVertexArray()

注意，开启 attribute 变量后，就不能再用 gl.vertexAttrib[1234]f() 系列函数向它传数据了，除非显式地关闭该 attribute 变量。实际上，无法（也不应该）同时使用这两个函数

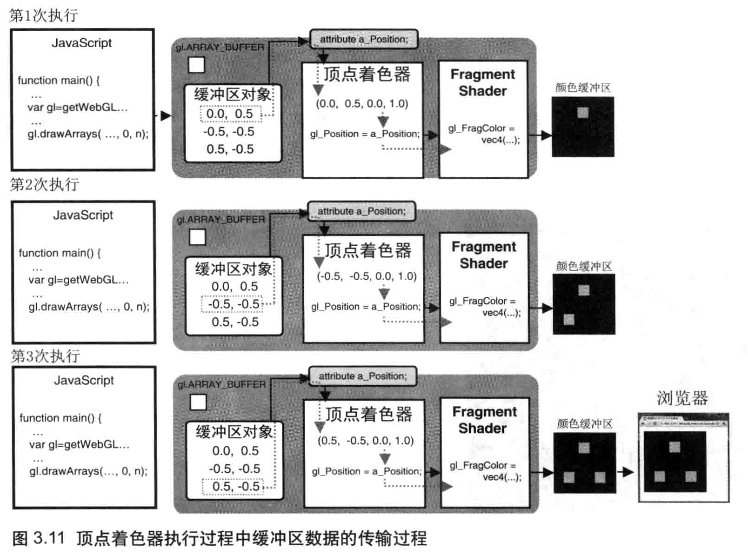
gl.drawArrays() 的第 2 个和第 3 个参数

之前 介绍过 gl.drawArrays() 方法规范，这里传入的 count 是 n（n 为 3）次，实际上顶点着色器执行了 3 次，存储在缓冲区中的顶点坐标数据被依次传给 attribute 变量

绘制基本图形

使用这些顶点绘制一个真正的图形，而不是单个的点

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
void main() {
  gl_Position = a_Position;
  // gl_PointSize = 10.0;
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
// 设置清除颜色并清空 canvas
 
// 绘制图形（三角形）
gl.drawArrays (gl.TRIANGLES, 0, n)

与绘制多个点 代码相同，只有两处不同：

• 在顶点着色器中，指定点的尺寸 gl_PointSize = 10.0; 被删去了。该语句只有在绘制单个点的时候才起作用
• gl.drawArrays() 方法的第 1 个参数从 gl.POINTS 改为了 gl.TRIANGLES

gl.drawArrays() 方法的第 1 个参数决定了 WebGL 的绘制方式，其可以绘制 7 种基本图形：

基本图形	mode 参数	描述
点	gl.POINTS	一系列点，绘制在 v0、v1、v2……处
线段	gl.LINES	一系列单独的线段，绘制在 (v0, v1)、(v2, v3)……处。 如果点的个数是奇数，则最后一个点被忽略
线条	gl.LINE_STRIP	一系列连接的线段，绘制在 (v0, v1)、(v1, v2)……处。 第 i(i>1) 个点是第 i-1 条线段的终点和第 i 条线段的起点，以此类推，最后一个点是最后一条线段的终点
回路	gl.LINE_LOOP	一系列连接的线段，与 gl.LINE_STRIP 相比，增加了一条从最后一个点到第一个点的线段。 即：绘制在 (v0, v1)、(v1, v2)……(vn, v0)处
三角形	gl.TRIANGLES	一系列单独的三角形，绘制在 (v0, v1, v2)、(v3, v4, v5)……处。 如果点的个数不是 3 的整数倍，则最后一个或两个点被忽略
三角带	gl.TRIANGLE_STRIP	一系列条带状的三角形，前 3 个点构成了第 1 个三角形，从第 2 个点开始的 3 个点构成了第 2 个三角形（该三角形与前一个三角形共享一条边），以此类推。 这些三角形绘制在 (v0, v1, v2)、(v2, v1, v3)、(v2, v3, v4)……处。 注意点的顺序：第 2 个三角形是 (v2, v1, v3) 而不是 (v1, v2, v3)，这是为了保持三角形的点按照递时针的顺序进行绘制
三角扇	gl.TRIANGLE_FAN	一系列三角形组成的类似扇形的图形，前 3 个点构成了第 1 个三角形，接下来的 1 个点和前一个三角形的最后一条边组成接下来的一个三角形，以此类推。 这些三角形绘制在 (v0, v1, v2)、(v0, v2, v3)、(v0, v3, v4)……处

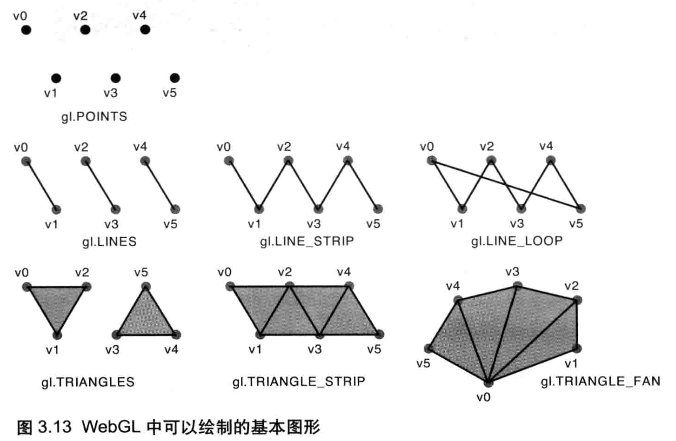
不管三维模型的形状多么复杂，都可以由小的三角形组成。实际上，可以使用以上这些最基本的图形来绘制出任何东西

仿射变换

平移、旋转和缩放，这样的操作称为变换（transformations）或仿射变换（affine transformations）

平移

为了平移一个三角形，需要对它的每一个顶点坐标的每个分量（x、y、z）加上三角形在对应轴上平移的距离

将点 p(x, y, z) 平移到 p’(x’, y’, z’)，在 X 轴、Y 轴、Z 轴三个方向上平移的距离分别为 Tx、Ty、Tz，其等式为：

$$\{\begin{array}{l}{x}^{\prime }=x+Tx\\ y^{\prime }=y+Ty\\ z^{\prime }=z+Tz\end{array}\text{\hspace{1em}(平移等式)}$$

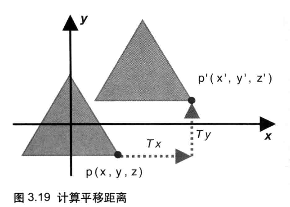
显然，这是一个逐顶点操作而非逐片元操作，上述修改应当发生在顶点着色器而不是片元着色器中

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position; // 顶点坐标
uniform vec4 u_Translation; // 平移距离
void main() {
  gl_Position = a_Position + u_Translation; // 顶点坐标 + 平移距离
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 将平移距离传输给定点着色器
const u_Translation = gl.getUniformLocation(gl.program, 'u_Translation')
if (!u_Translation) {
  console.error(`uniform 变量 'u_Translation' 位置获取失败`)
  return
}
gl.uniform4f(u_Translation, 0.5, 0.5, 0.0, 0.0)
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）

• uniform vec4 u_Translation;
  • 因为 Tx、Ty、Tz 对于所有顶点来说是固定（一致）的，所以使用 uniform 变量
  • GLSL ES 中的赋值和运算操作只能发生在相同类型的变量之间，所以使用和 a_Position 相同的类型 vec4
• gl.uniform4f(u_FragColor, 0.5, 0.5, 0.0, 0.0)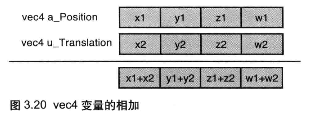
  • 
  • 第 4 个值是齐次坐标，这里传 0 保证相加后还是 1

旋转

旋转必须指明：

• 旋转轴：图形将围绕旋转轴旋转
• 旋转方向：顺时针或逆时针
• 旋转角度：图形旋转经过的角度

其实旋转角度的正负可以表示旋转方向

约定：如果旋转角度是正值，观察者在 Z 轴正半轴某处，视线沿着 Z 轴负方向进行观察，那么看到的物体就是逆时针旋转的

也可以使用右手来确认旋转方向：右手握拳，大拇指伸直并使其指向旋转轴的正方向，那么右手其余几个手指就指明了旋转的方向

这种情况可称作正旋转（positive rotation），也叫右手法则旋转（right-hand-rule rotation）

假设将点 p(x, y, z) 沿 Z 轴旋转 $\beta$ 角度之后变为了 p’(x’, y’, z’)

其中：

$$\{\begin{array}{l}x=r\cos \alpha \\ y=r\sin \alpha \end{array}\text{\hspace{1em}(等式 1)}$$

同理：

$$\{\begin{array}{l}{x}^{\prime }=r\cos (\alpha +\beta )\\ y^{\prime }=r\sin (\alpha +\beta )\end{array}$$

上式利用三角函数两角和差公式，可得：

$$\{\begin{array}{l}{x}^{\prime }=r(\cos \alpha \cos \beta -\sin \alpha \sin \beta ))\\ y^{\prime }=r(\sin \alpha \cos \beta +\cos \alpha \sin \beta ))\end{array}$$

将等式 1 代入上式，消除 $r$ 和 $\alpha$，可得：

$$\{\begin{array}{l}{x}^{\prime }=x\cos \beta -y\sin \beta \\ y^{\prime }=x\sin \beta +y\cos \beta \\ z^{\prime }=z\end{array}\text{\hspace{1em}(沿 Z 轴旋转等式)}$$

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position; // 顶点坐标
uniform vec2 u_CosBSinB; // 旋转角度：[cosB, sinB]
void main() {
  gl_Position.x = a_Position.x * u_CosBSinB.x - a_Position.y * u_CosBSinB.y;
  gl_Position.y = a_Position.x * u_CosBSinB.y + a_Position.y * u_CosBSinB.x;
  gl_Position.z = a_Position.z;
  gl_Position.w = a_Position.w;
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 将旋转角度数据传输给着色器
const angle = 90 // 角度制
const radian = Math.PI * angle / 180 // 弧度制
const u_CosBSinB = gl.getUniformLocation(gl.program, 'u_CosBSinB')
if (!u_CosBSinB) {
  console.error(`uniform 变量 'u_CosBSinB' 位置获取失败`)
  return
}
gl.uniform2f(u_CosBSinB, Math.cos(radian), Math.sin(radian))
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）

之前进行平移变换时，齐次坐标的 x、y、z、w 分量是作为整体进行加法运算的，而进行旋转变换时，为了计算沿 Z 轴旋转等式，需要单独访问 a_Position 的每个分量：

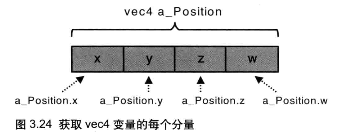
缩放

缩放必须指明：

• 缩放原点：图形以哪个点为中心进行缩放
• 缩放系数（缩放因子）：图形缩放的比例
  • $(1,+\infty ]$：放大
  • 1：不变
  • $(0,1)$：缩小
  • 0：缩小到不可见
  • 负数：翻转

为了简单将缩放原点定为 (0, 0, 0)，将点 p(x, y, z) 缩放到 p’(x’, y’, z’)，在 X 轴、Y 轴、Z 轴三个方向上的缩放系数分别为 Sx、Sy、Sz，其等式为：

$$\{\begin{array}{l}{x}^{\prime }=x\times Sx\\ y^{\prime }=y\times Sy\\ z^{\prime }=z\times Sz\end{array}\text{\hspace{1em}((0, 0, 0) 缩放等式)}$$

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position; // 顶点坐标
uniform vec4 u_Scale; // 缩放系数
void main() {
  gl_Position = a_Position * u_Scale; // 顶点坐标 * 缩放系数
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 将缩放系数传输给定点着色器
const u_Scale = gl.getUniformLocation(gl.program, 'u_Scale')
if (!u_Scale) {
  console.error(`uniform 变量 'u_Scale' 位置获取失败`)
  return
}
gl.uniform4f(u_Scale, 0.5, 0.5, 0.5, 1.0)
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）

矢量相乘同理于矢量相加，会分别相乘对应分量

变换矩阵：平移

对于简单的变换，可以使用数学表达式来实现，但当情形逐渐变得复杂时，很快就会发现利用表达式运算相当繁琐。如“旋转后平移”等复合变换就需要叠加相应的等式，获得一个新的等式，然后在顶点着色器中实现

如果这样做，每次需要进行一次新的变换，就需要重新求取一个新的等式，然后实现一个新的着色器，这当然很不科学。变换矩阵（transformation matrix）解决了这个问题，它非常适合操作计算机图形

将矩阵右乘矢量 结果与平移等式 进行比较：

$$\begin{array}{l}\begin{array}{l}{x}^{\prime }=ax+by+cz+d\\ x^{\prime }=x+Tx\end{array}\}设a=1,b=0,c=0,d=Tx，两式完全相同\\ \\ \begin{array}{l}{y}^{\prime }=ex+fy+gz+h\\ y^{\prime }=y+Ty\end{array}\}设e=0,f=1,g=0,h=Ty，两式完全相同\\ \\ \begin{array}{l}{z}^{\prime }=ix+jy+kz+l\\ z^{\prime }=z+Tz\end{array}\}设i=0,j=0,k=1,l=Tz，两式完全相同\\ \\ \begin{array}{l}w=mx+ny+oz+p\\ w=1\end{array}\}设m=0,n=0,o=1,p=1，两式完全相同\end{array}$$

得出：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& Tx\\ 0& 1& 0& Ty\\ 0& 0& 1& Tz\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\text{\hspace{1em}(平移矩阵)}$$

这个矩阵就是变换矩阵（transformation matrix），因为它将右侧的矢量 (x, y, z) “变换”为了左侧的矢量 (x’, y’, z’)。这个变换矩阵进行的变换是一次平移，所以也称为平移矩阵（translation matrix）

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
uniform mat4 u_xformMatrix; // 变换矩阵
void main() {
  gl_Position = u_xformMatrix * a_Position;
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 定义变换矩阵
const Tx = 0.5, Ty = 0.5, Tz = 0.0
// 注意 WebGL 中矩阵是列主序的
const xformMatrix = new Float32Array([
  1.0, 0.0, 0.0, 0.0,
  0.0, 1.0, 0.0, 0.0,
  0.0, 0.0, 1.0, 0.0,
  Tx, Ty, Tz, 1.0
])
 
// 传入变换矩阵
const u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix')
if (!u_xformMatrix) {
  console.error(`uniform 变量 'u_xformMatrix' 位置获取失败`)
  return
}
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix)
 
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）

• uniform mat4 u_xfromMatrix;
  • a_Position 是 4 维的矢量，要做计算，u_xfromMatrix 必须是 4x4 的矩阵
• gl_Position = u_xfromMatrix * a_Position;
  • <新坐标> = <变换矩阵> * <旧坐标>
  • 变换矩阵在三维计算机图形学中应用得如此广泛，以致于着色器本身就实现了矩阵和矢量相乘的功能
• 注意 WebGL 中矩阵是列主序的 ^lzs
  • 数组存储（表示）矩阵有两种方式：按行主序（row major order）和按列主序（column major order）
  • 
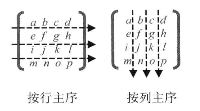
  • WebGL 和 OpenGL 一样，矩阵元素是按列主序存储在数组中的。即：[a, e, i, m, b, f, j, n, c, g, k, o, d, h, l, p]
• gl.uniformMatrix4fv(location, transpose, array)：将 array 表示的 4x4 矩阵分配给由 location 指定的 uniform 变量
  • location：uniform 变量的存储位置
  • transpose：是否转置矩阵（转置操作将交换矩阵的行和列），WebGL 实现没有提供矩阵转置的方法，所以该参数必须设为 false
  • array：待传输的类型化数组，4×4 矩阵按列主序存储在其中
  • 错误
    • INVALID_OPERATION：不存在当前程序对象
    • INVALID_VALUE：transpose 不为 false，或者 array 的长度小于 16

变换矩阵：旋转

将矩阵右乘矢量结果与沿 Z 轴旋转等式 进行比较：

$$\begin{array}{l}\begin{array}{l}{x}^{\prime }=ax+by+cz\\ x^{\prime }=x\cos \beta -y\sin \beta \end{array}\}设a=\cos \beta ,b=-\sin \beta ,c=0，两式完全相同\\ \\ \begin{array}{l}{y}^{\prime }=dx+ey+fz\\ y^{\prime }=x\sin \beta +y\cos \beta \end{array}\}设d=\sin \beta ,e=\cos \beta ,f=0，两式完全相同\\ \\ \begin{array}{l}{z}^{\prime }=gx+hy+iz\\ z^{\prime }=z\end{array}\}设g=0,h=0,f=1，两式完全相同\end{array}$$

得出旋转矩阵（rotation matrix）：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}\cos \beta & -\sin \beta & 0\\ \sin \beta & \cos \beta & 0\\ 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\end{array}\right]\text{\hspace{1em}(沿 Z 轴 3x3 旋转矩阵)}$$

上面的旋转矩阵（3×3 矩阵）与平移矩阵（4×4 矩阵）的阶数不同，难以运算，需要对其升阶，得出：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}\cos \beta & -\sin \beta & 0& 0\\ \sin \beta & \cos \beta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\text{\hspace{1em}(沿 Z 轴旋转矩阵)}$$

// 顶点着色器程序（GLSL ES）
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 定义变换矩阵
const angle = 90 // 角度制
const radian = Math.PI * angle / 180 // 弧度制
const cosB = Math.cos(radian), sinB = Math.sin(radian)
// 注意 WebGL 中矩阵是列主序的
const xformMatrix = new Float32Array([
  cosB, sinB, 0.0, 0.0,
  -sinB, cosB, 0.0, 0.0,
  0.0, 0.0, 1.0, 0.0,
  0.0, 0.0, 0.0, 1.0
])
 
// 传入变换矩阵
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）

变换矩阵：缩放

同理将矩阵右乘矢量结果与 (0, 0, 0) 缩放等式 进行比较，得出缩放矩阵（scaling matrix）：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}Sx& 0& 0& 0\\ 0& Sy& 0& 0\\ 0& 0& Sz& 0\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\text{\hspace{1em}((0, 0, 0) 缩放矩阵)}$$

// 顶点着色器程序（GLSL ES）
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 定义变换矩阵
const Sx = 0.5, Sy = 0.5, Sz = 0.5
// 注意 WebGL 中矩阵是列主序的
const xformMatrix = new Float32Array([
  Sx, 0.0, 0.0, 0.0,
  0.0, Sy, 0.0, 0.0,
  0.0, 0.0, Sz, 0.0,
  0.0, 0.0, 0.0, 1.0
])
 
// 传入变换矩阵
// 设置清除颜色并清空 canvas
// 绘制图形（三角形）