004.高级变换与动画基础

复合变换

矩阵变换库：cuon-matrix.js

为了简化编程，大多数 WebGL 开发者都使用矩阵操作函数库来隐藏矩阵计算的细节。目前已经有一些开源的矩阵库，在本书中，将使用一个专为本书编写的矩阵变换函数库：cuon-matrix.js

之前手动编写矩阵：

const angle = 90 // 角度制
const radian = Math.PI * angle / 180 // 弧度制
const cosB = Math.cos(radian), sinB = Math.sin(radian)
// 注意 WebGL 中矩阵是列主序的
const xformMatrix = new Float32Array([
  cosB, sinB, 0.0, 0.0,
  -sinB, cosB, 0.0, 0.0,
  0.0, 0.0, 1.0, 0.0,
  0.0, 0.0, 0.0, 1.0
])
// ...
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix)

使用 cuon-matrix.js：

const angle = 90 // 角度制
// 为旋转矩阵创建 Matrix4 对象
const xformMatrix = new Matrix4()
// 将 xformMatrix 设置为旋转矩阵
xformMatrix.setRotate(angle, 0, 0, 1)
// 将旋转矩阵传输给顶点着色器
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix.elements)

Matrix4 对象所支持的属性和方法：

• elements：类型化数组（Float32Array），包含了 Matrix4 实例的矩阵元素（按列主序）
• setIdentity()：将 Matrix4 实例初始化为单位矩阵
  • 单位阵在矩阵乘法中的行为，就像数字 1 在乘法中的行为一样。即：将一个矩阵乘以单位阵，得到的结果和原矩阵完全相同
  • 在单位阵中，对角线上的元素为 1，其余的元素为 0
• setTranslate(x, y, z)：将 Matrix4 实例设置为平移变换矩阵
  • x、y、z：在对应轴平移的距离
  • 正数往正方向平移；负数往负方向平移
• setRotate(angle, x, y, z)：将 Matrix4 实例设置为旋转变换矩阵
  • angle：旋转角度（角度制），正负代表旋转方向（详见）
  • x、y、z：旋转轴，无需归一化
• setScale(x, y, z)：将 Matrix4 实例设置为缩放变换矩阵
  • x、y、z：在对应轴的缩放系数（缩放因子）
  • 缩放系数不同的值可以实现放大、缩小、翻转（详见）
• translate(x, y, z)：将 Matrix4 实例乘以一个平移变换矩阵
• rotate(angle, x, y, z)：将 Matrix4 实例乘以一个旋转变换矩阵
• scale(x, y, z)：将 Matrix4 实例乘以一个缩放变换矩阵
• set(m)：将 Matrix4 实例设置为 m，m 必须也是一个 Matrix4 实例

Matrix4 对象有两种方法：

• 含有前缀 set：根据参数计算出变换矩阵，然后将变换矩阵写入到自身中（不管自身原来的数据）
• 不含：根据参数计算出变换矩阵，然后将自身与刚刚计算得到的变换矩阵相乘，然后把最终得到的结果写入自身

平移，然后旋转

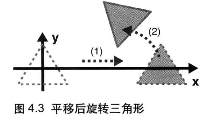
1. 平移：$<“平移”后的坐标>=<平移矩阵>\times <原始坐标>$
2. 然后旋转：$<“平移后旋转”后的坐标>=<旋转矩阵>\times <“平移”后的坐标>$

将两个等式组合：$<“平移后旋转”后的坐标>=<旋转矩阵>\times (<平移矩阵>\times <原始坐标>)$

矩阵的乘法不符合交换律，但符合结合律（矢量和矩阵运算的性质），所以上式等于：$<“平移后旋转”后的坐标>=(<旋转矩阵>\times <平移矩阵>)\times <原始坐标>$

可以在 JS 中计算 $<旋转矩阵>\times <平移矩阵>$（矩阵和矩阵相乘），然后将得到的矩阵传入顶点着色器，就可以把多个变换复合起来了

可以看到，“先平移后旋转”的顺序与构造模型矩阵 $<旋转矩阵>\times <平移矩阵>$ 的顺序是相反的

一个模型可能经过多次变换，将这些变换全部复合成一个等效的变换，就得到了模型变换（model transformation），或称建模变换（modeling transformation），相应地，模型变换的矩阵称为模型矩阵（model matrix）

// 顶点着色器程序（GLSL ES）
const vertexShaderSource = `
attribute vec4 a_Position;
uniform mat4 u_ModelMatrix; // 模型矩阵
void main() {
  gl_Position = u_ModelMatrix * a_Position; // <模型矩阵> x <原始坐标>
}
`
 
// 片元着色器程序（GLSL ES）
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
 
// 定义模型矩阵
const Tx = 0.5
const angle = 60.0
const modelMatrix = new Matrix4()
// 注意矩阵相乘的顺序
modelMatrix.setRotate(angle, 0, 0, 1) // <旋转矩阵>
modelMatrix.translate(Tx, 0, 0) // <旋转矩阵> x <平移矩阵>
 
// 传入模型矩阵
const u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix')
if (!u_ModelMatrix) {
  console.error(`uniform 变量 'u_ModelMatrix' 位置获取失败`)
  return
}
gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
 
// 设置清除颜色并清空 canvas
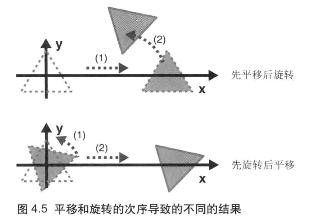
// 绘制图形（三角形）

一定要注意先后顺序，不同顺序的结果是完全不同的：

动画

按照恒定的速度（45 度/秒）旋转三角形

动画的本质就是：不断擦除和重绘三角形，并且在每次重绘时改变其角度

反复调用

为了使三角形动起来，需要反复进行以下两步：

1. 更新三角形的当前角度
2. 根据当前角度绘制三角形

浏览器提供的 requestAnimationFrame() 方法保证了在下一帧调用，可以实现流畅地 JS 动画

// 顶点着色器程序（GLSL ES）
// 片元着色器程序（GLSL ES）
 
// 旋转速度（度/秒）
const angleStep = 45
// 当前角度
let curAngle = 0
 
// 获取 canvas 元素
// 获取 WebGL 上下文
// 初始化着色器
// 设置顶点位置
// 设置清除颜色并清空 canvas
// 定义模型矩阵
 
// 开始绘制三角形
const tick = () => {
  curAngle = animate(curAngle) // 更新旋转角度
  draw(gl, n, curAngle, modelMatrix, u_ModelMatrix) // 在画布绘制
  requestAnimationFrame(tick) // 请求浏览器在下一帧调用 tick
}
tick()

更新三角形的当前角度

requestAnimationFrame() 方法保证了在下一帧调用，但是用户电脑可能是 60FPS，也可能是 120FPS，而且浏览器标签页失焦也会挂起 requestAnimationFrame()，无法知道上一次调用和本次调用直接过了多长时间（而且间隔也不是固定的）

那么每次调用 tick() 时简单地加上一个固定的角度值就会导致不可控制的加速或减速的旋转效果，所以需要手动根据本次调用与上次调用之间的时间间隔来决定这一帧的旋转角度比上一帧大出多少

let last = Date.now() // 记录上一次调用 tick() 的时间
function animate(angle) {
  const now = Date.now() // 当前调用的时间
  const elapsed = now - last // 时间间隔（毫秒）
  last = now // 更新上一次调用的时间，方便下次计算
  const newAngle = angle + (angleStep * elapsed) / 1000 // 计算现在的角度
  return newAngle % 360
}

根据当前角度绘制三角形

function draw(gl, n, angle, modelMatrix, u_ModelMatrix) {
  modelMatrix.setRotate(angle, 0, 0, 1) // 设置旋转矩阵
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements) // 传输给顶点着色器
  gl.clear(gl.COLOR_BUFFER_BIT) // 使用之前设置的颜色清除 <canvas>
  gl.drawArrays(gl.TRIANGLES, 0, n) // 绘制三角形
}