035.单调栈-下

前置知识：单调栈-上

除了单调栈最经典的用法之外，在很多问题里单调栈还可以维持求解答案的可能性

1. 单调栈里的所有对象按照规定好的单调性来组织
2. 当某个对象进入单调栈时，会从栈顶开始依次淘汰单调栈里对后续求解答案没有帮助的对象
3. 每个对象从栈顶弹出的时结算当前对象参与的答案，随后这个对象不再参与后续求解答案的过程
4. 其实是先有对题目的分析！进而发现单调性，然后利用单调栈的特征去实现

备注 §

单调栈可以和很多技巧交叉使用！比如：动态规划 + 单调栈优化，会在【扩展】课程里讲述

题目1.最大宽度坡 §

题目描述 §

给定一个整数数组 A，坡是元组 (i, j)，其中  i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。

找出 A 中的坡的最大宽度，如果不存在，返回 0 。

提示：

• 2 <= A.length <= 50000
• 0 <= A[i] <= 50000

测试链接 §

962.最大宽度坡

答案 §

func maxWidthRamp(nums []int) int {
	stack := []int{0}
	n := len(nums)
	// 栈底 -> 栈顶：大 -> 小
	// 收集到的都是可能为答案的左位置
	// [小 大   右位置]
	// 如果能以“大”为左位置，“右位置”为右位置得到答案
	// 则说明“右位置”比“大”要大
	// 那以“小”为左位置，“右位置”为右位置得到答案会更宽
	// 所以答案不可能以“大”为左位置
	for i := 1; i < n; i++ {
		if nums[stack[len(stack)-1]] > nums[i] {
			stack = append(stack, i)
		}
	}
 
	ans := 0
	for i := n - 1; i >= 0; i-- {
		// 以 i 为右位置，栈中元素都是可能作为左位置的
		// 左位置 <= 右位置：结算答案
		// 并弹出栈：因为这个左位置已经和最右的右位置结算过了
		// 之后它（左位置）不可能得到更好的答案了
		for len(stack) > 0 && nums[stack[len(stack)-1]] <= nums[i] {
			ans = max(ans, i-stack[len(stack)-1])
			stack = stack[:len(stack)-1]
		}
	}
	return ans
}

复杂度 §

• 时间复杂度：$O(n)$，所有元素只进栈出栈一次
• 空间复杂度：$O(n)$，单调栈的空间

题目2.去除重复字母保证剩余字符串的字典序最小 §

题目描述 §

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1：

输入：s = "bcabc"

输出："abc"

示例 2：

输入：s = "cbacdcbc"

输出："acdb"

提示：

• 1 <= s.length <= 10^4
• s 由小写英文字母组成

测试链接 §

• 316.去除重复字母
• 1081.不同字符的最小子序列

答案 §

const (
	MAXN = 26
)
 
var (
	stack     = [MAXN]byte{} // 单调栈
	stackSize = 0
	cnts      = [MAXN]int{}  // 词频
	entered   = [MAXN]bool{} // 是否在栈中
)
 
// 去除重复字母 == 保留需要字符
func removeDuplicateLetters(s string) string {
	reset()
	n := len(s)
	for i := 0; i < n; i++ {
		cnts[s[i]-'a']++
	}
	for i := 0; i < n; i++ {
		if !entered[s[i]-'a'] { // 已经在栈中，不再处理
			// 当前元素字典序小于栈顶元素，且之后还有栈顶元素
			// 就弹出栈顶元素
			for stackSize > 0 && stack[stackSize-1] > s[i] && cnts[stack[stackSize-1]-'a'] > 0 {
				entered[stack[stackSize-1]-'a'] = false
				stackSize--
			}
			stack[stackSize] = s[i]
			stackSize++
			entered[s[i]-'a'] = true
		}
		cnts[s[i]-'a']--
	}
	return string(stack[:stackSize])
}
 
func reset() {
	stackSize = 0
	clear(cnts[:MAXN])
	clear(entered[:MAXN])
}

题目3.大鱼吃小鱼 §

题目描述 §

给定一个数组 arr，每个值代表鱼的体重

每一轮，每条鱼都会吃掉右边离自己最近比自己体重小的鱼，每条鱼向右找只吃一条

但是吃鱼这件事是同时发生的，也就是同一轮在 A 吃掉 B 的同时，A 也可能被别的鱼吃掉

如果有多条鱼在当前轮找到的是同一条小鱼，那么在这一轮，这条小鱼同时被这些大鱼吃

请问多少轮后，鱼的数量就固定了

示例 1：

输入：arr = [8, 3, 1, 5, 6, 7, 2, 4]

输出：4

解释：

第一轮：8 吃 3；3 吃 1；5、6、7 吃 2；4 没有被吃。数组剩下 [8, 5, 6, 7, 4]

第二轮：8 吃 5；5、6、7 吃 4。数组剩下 [8, 6, 7]

第三轮：8 吃 6。数组剩下 [8, 7]

第四轮：8 吃 7。数组剩下 [8]

过程结束，返回 4

测试链接 §

大鱼吃小鱼

思路 §

因为鱼往右吃，所以从右往左遍历，累计轮次

答案 §

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 1e5 + 1
)
 
var (
	arr       = [MAXN]int{}
	n         int
	stack     = [MAXN][2]int{} // [鱼的体重, 要行动的轮数]
	stackSize = 0
)
 
func main() {
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		for i := 0; i < n; i++ {
			in.Scan()
			arr[i], _ = strconv.Atoi(in.Text())
		}
		fmt.Fprintln(out, turns())
	}
	out.Flush()
}
 
func turns() int {
	stackSize = 0
	ans := 0
	for i := n - 1; i >= 0; i-- {
		curTurns := 0
		for stackSize > 0 && arr[i] > stack[stackSize-1][0] {
			curTurns = max(curTurns+1, stack[stackSize-1][1])
			stackSize--
		}
		stack[stackSize][0] = arr[i]
		stack[stackSize][1] = curTurns
		stackSize++
		ans = max(ans, curTurns)
	}
	return ans
}
 
// 牛客 go 版本太低，没有内置的 max 函数
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

复杂度 §

• 时间复杂度：$O(n)$，所有元素只进栈出栈一次
• 空间复杂度：$O(n)$，单调栈的空间

题目4.统计全 1 子矩形 §

题目描述 §

给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

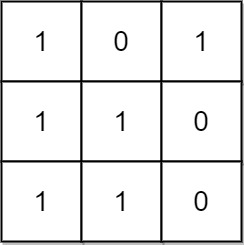
输入：mat = [[1,0,1],[1,1,0],[1,1,0]]

输出：13

解释：

有 6 个 1x1 的矩形

有 2 个 1x2 的矩形

有 3 个 2x1 的矩形

有 1 个 2x2 的矩形

有 1 个 3x1 的矩形

矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13

提示：

• 1 <= m, n <= 150
• mat[i][j] 仅包含 0 或 1

测试链接 §

1504.统计全 1 子矩形

思路 §

数组压缩技巧：求以每一行为底的结果

要先理解：最大矩形 这道题

答案 §

const (
	MAXN = 151
)
 
var (
	height    = [MAXN]int{}
	stack     = [MAXN]int{}
	stackSize = 0
	n         int
	m         int
)
 
func numSubmat(mat [][]int) int {
	n = len(mat)
	m = len(mat[0])
	ans := 0
	for i := 0; i < n; i++ {
		// 数组压缩技巧：求以每一行为底的结果
		for j := 0; j < m; j++ {
			if mat[i][j] == 1 {
				height[j] += 1
			} else {
				height[j] = 0
			}
		}
		ans += countFromBottom()
	}
	for i := 0; i < m; i++ {
		height[i] = 0
	}
	return ans
}
 
// 比如：
//
//	           1
//	           1
//	           1         1
//	 1         1         1
//	 1         1         1
//	 1         1         1
//
//	 3  ....   6   ....  8
//	left      cur        i
//
// 如上图，假设 6 位置从栈中弹出，6 位置的高度为 6（上面 6 个 1）
// 6 位置的左边、离 6 位置最近且小于的是 3 位置(left)，高度是 3
// 6 位置的右边、离 6 位置最近且小于的是 8 位置(i)，高度是 4
// 此时我们求什么？
// 1) 求在 4~7 范围上必须以高度 6 作为高的矩形有几个？
// 2) 求在 4~7 范围上必须以高度 5 作为高的矩形有几个？
// 也就是说，<=4 的高度一律不求，>6 的高度一律不求！
// 其他位置也会从栈里弹出，等其他位置弹出的时候去求！
// 那么在 4~7 范围上必须以高度 6 作为高的矩形有几个？如下：
// 4..4  4..5  4..6  4..7
// 5..5  5..6  5..7
// 6..6  6..7
// 7..7
// 10 个！什么公式？
// 4...7 范围的长度为 4，那么数量就是: 4*5/2
// 同理在 4~7 范围上，必须以高度 5 作为高的矩形也是这么多
// 所以 cur 从栈里弹出时产生的数量:
// (cur位置的高度-Max{left位置的高度,i位置的高度}) * (i-left-1)*(i-left)/2
func countFromBottom() int {
	stackSize = 0
	ans := 0
	for i := 0; i < m; i++ {
		for stackSize > 0 && height[stack[stackSize-1]] >= height[i] {
			cur := stack[stackSize-1]
			stackSize--
			if height[cur] > height[i] {
				// 只有 height[cur] > height[i] 才结算
				// 如果是因为 height[cur] == height[i] 导致 cur 位置从栈中弹出
				// 那么不结算！等 i 位置弹出的时候再说！
				// 后面会修正
				// 上一节课讲了很多这种相等时候的处理，比如"柱状图中最大的矩形"问题
				left := -1
				bottom := 0
				if stackSize > 0 {
					left = stack[stackSize-1]
					bottom = height[left]
				}
				bottom = max(bottom, height[i])
				length := i - left - 1
				ans += (height[cur] - bottom) * length * (length + 1) / 2
			}
		}
		stack[stackSize] = i
		stackSize++
	}
	for stackSize > 0 {
		cur := stack[stackSize-1]
		stackSize--
		left := -1
		bottom := 0
		if stackSize > 0 {
			left = stack[stackSize-1]
			bottom = height[left]
		}
		length := m - left - 1
		ans += (height[cur] - bottom) * length * (length + 1) / 2
	}
	return ans
}