034.单调栈-上

前置知识：用数组方式实现栈

单调栈 §

最经典的用法是解决如下问题 §

每个位置都求：

• 当前位置的左侧比当前位置的数字小，且距离最近的位置在哪
• 当前位置的右侧比当前位置的数字小，且距离最近的位置在哪

（单调栈大压小）

或者

每个位置都求：

• 当前位置的左侧比当前位置的数字大，且距离最近的位置在哪
• 当前位置的右侧比当前位置的数字大，且距离最近的位置在哪

（单调栈小压大）

思路 §

以获取每个位置左右最近的比当前位置数字小的位置为例

遍历数组，依次入栈，单调栈保持大压小，如果违反大压小，则依次弹出栈顶元素并结算

// 遍历阶段
for i := 0; i < n; i++ {
	// 违反大压小，就弹出栈顶元素并结算
	for stackSize > 0 && arr[stack[stackSize-1]] >= arr[i] {
		// 弹出栈顶元素
		stackSize--
		top = stack[stackSize]
		// 栈顶元素左侧最近且小于栈顶元素的位置是弹出当前栈顶元素的栈顶元素
		left[top] = -1
		if stackSize > 0 {
			left[top] = stack[stackSize-1]
		}
		// 栈顶元素右侧最近且小于栈顶元素的位置是当前遍历到的位置，即：使栈顶元素弹出的元素位置
		right[top] = i
	}
	// 压入当前遍历到的元素
	stack[stackSize] = i
	stackSize++
}

遍历完数组后，要结算栈中的元素（依次从栈顶进行结算）

// 清算阶段
for stackSize > 0 { // 栈不空
	// 弹出栈顶元素
	stackSize--
	top = stack[stackSize]
	// 栈顶元素左侧最近且小于栈顶元素的位置是弹出当前栈顶元素的栈顶元素
	left[top] = -1
	if stackSize > 0 {
		left[top] = stack[stackSize-1]
	}
	// 因为遍历了一遍数组，都没有将这些元素弹出，则说明栈顶元素右侧最近且小于栈顶元素的位置不存在
	right[top] = -1
}

当数组无重复值时，经过上面的遍历阶段 + 清算阶段，所有的答案都已求解正确

但是当数组有重复值时，因为两数相等时，也弹出栈，所以右记录的是第一个等于当前元素的下标，而不是第一个小于当前元素的下标

所以要加一个修正阶段，最右的相等元素的右记录一定是对的，而其他的相等元素的右记录是下一个相等元素位置，从右往左修正就能修正对

// 修正阶段：数组有重复值才需要，无重复值则什么都不会改变
// 左侧的答案不需要修正，一定是正确的，只有右侧答案需要修正
// 从右往左修正，n-1 位置的右侧答案一定是 -1，不需要修正
for i := n - 2; i >= 0; i-- {
	// 有右侧值，且右侧值与当前值相同，说明答案是错的，要修正
	if right[i] != -1 && arr[right[i]] == arr[i] {
		// 相等元素最右侧的答案是对的
		// 从右往左遍历，修正成右侧相等元素的答案就是正确的答案
		right[i] = right[right[i]]
	}
}

复杂度 §

求解过程中，单调栈所有调整的总代价为 $O(n)$，单次操作的均摊代价为 $O(1)$，因为所有元素均只入栈出栈一次

空间复杂度：$O(n)$，单调栈的空间

备注 §

要注意不同题目中相等值出现时的处理（后续的题目），虽然严格的模板套都能得出正确的答案，但是太死板，应该根据题目灵活变通

这是单调栈最经典的用法，可以解决很多题目，下节课将继续介绍其他的用法

单调栈可以和很多技巧交叉使用！比如：动态规划 + 单调栈优化，会在【扩展】课程里讲述

题目1.单调栈最经典用法的模版 §

题目描述 §

给定一个可能含有重复值的数组 arr，找到每一个 i 位置左边和右边离 i 位置最近且值比 arr[i] 小的位置，如果不存在，则值为 -1。返回所有位置相应的信息。

测试链接 §

单调栈结构(进阶)

答案 §

package main
 
import (
	"bufio"
	"fmt"
	"os"
	"strconv"
)
 
const (
	MAXN = 1000000
)
 
var (
	arr      = [MAXN]int{}
	left     = [MAXN]int{}
	right    = [MAXN]int{}
	n        int
	stack    = [MAXN]int{}
	stackSize int
)
 
func main() {
	in := bufio.NewScanner(os.Stdin)
	in.Split(bufio.ScanWords)
	out := bufio.NewWriterSize(os.Stdout, 4096)
	for in.Scan() {
		n, _ = strconv.Atoi(in.Text())
		for i := 0; i < n; i++ {
			in.Scan()
			arr[i], _ = strconv.Atoi(in.Text())
		}
		compute()
		for i := 0; i < n; i++ {
			fmt.Fprintln(out, left[i], right[i])
		}
	}
	out.Flush()
}
 
func compute() {
	stackSize = 0
	// 栈顶元素
	top := 0
	// 遍历阶段
	for i := 0; i < n; i++ {
		// 大压小
		for stackSize > 0 && arr[stack[stackSize-1]] >= arr[i] {
			stackSize--
			top = stack[stackSize]
			left[top] = -1
			if stackSize > 0 {
				left[top] = stack[stackSize-1]
			}
			right[top] = i
		}
		stack[stackSize] = i
		stackSize++
	}
	// 清算阶段
	for stackSize > 0 {
		stackSize--
		top = stack[stackSize]
		left[top] = -1
		if stackSize > 0 {
			left[top] = stack[stackSize-1]
		}
		right[top] = -1
	}
	// 修正阶段
	// 左侧的答案不需要修正，一定是正确的，只有右侧答案需要修正
	// 从右往左修正，n-1 位置的右侧答案一定是 -1，不需要修正
	for i := n - 2; i >= 0; i-- {
		if right[i] != -1 && arr[right[i]] == arr[i] {
			right[i] = right[right[i]]
		}
	}
}

题目2.每日温度 §

题目描述 §

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

测试链接 §

739.每日温度

思路 §

左记录不关心，当相等的时候，也压入单调栈

答案 §

func dailyTemperatures(temperatures []int) []int {
	ans := make([]int, len(temperatures))
	stack := []int{}
 
	for i, val := range temperatures {
		for len(stack) > 0 && val > temperatures[stack[len(stack)-1]] {
			top := stack[len(stack)-1]
			stack = stack[:len(stack)-1]
			ans[top] = i - top
		}
		stack = append(stack, i)
	}
 
	return ans
}

题目3.子数组的最小值之和 §

题目描述 §

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

由于答案可能很大，因此返回答案模 10^9 + 7。

示例 1：

输入：arr = [3,1,2,4]

输出：17

解释：

子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]

最小值为 3，1，2，4，1，1，2，1，1，1，和为 17

提示：

• 1 <= arr.length <= 3 * 10^4
• 1 <= arr[i] <= 3 * 10^4

测试链接 §

907.子数组的最小值之和

思路 §

如果遍历子数组（$O(n!)$）算累加和的话必超时，n 的范围是 $10^4$，所以时间复杂度最多到 $O(n^2)$（根据数据量猜解法）

答案可能很大，要模一个大质数，运算过程可能溢出，需要使用 同余原理

使用单调栈可以求出左侧和右侧第一个小于当前数的位置，在这个位置之内的所有子数组的最小值都是当前值

有 (cur-left)*(right-cur) 个子数组，(cur-left)：开头的个数；(right-cur)：结尾的个数

相等的时候分开算

答案 §

const (
	MOD = 1e9 + 7
)
 
func sumSubarrayMins(arr []int) int {
	n := len(arr)
	stack := make([]int, 0, n)
	ans := 0
	for i, num := range arr {
		for len(stack) > 0 && num <= arr[stack[len(stack)-1]] {
			top := stack[len(stack)-1]
			stack = stack[:len(stack)-1]
			left := -1
			if len(stack) > 0 {
				left = stack[len(stack)-1]
			}
			ans = (ans + (top-left)*(i-top)*arr[top]) % MOD
		}
		stack = append(stack, i)
	}
	for i := len(stack) - 1; i >= 0; i-- {
		top := stack[i]
		left := -1
		if i-1 >= 0 {
			left = stack[i-1]
		}
		ans = (ans + (top-left)*(n-top)*arr[top]) % MOD
	}
	return ans
}

题目4.柱状图中最大的矩形 §

题目描述 §

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1：

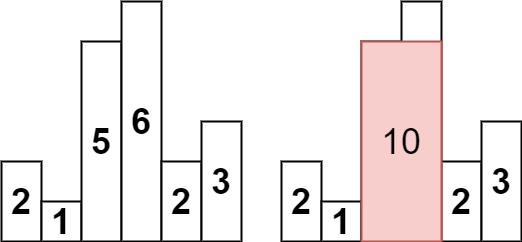
输入：heights = [2,1,5,6,2,3]

输出：10

解释：最大的矩形为图中红色区域，面积为 10

测试链接 §

84.柱状图中最大的矩形

思路 §

严格求小于，虽然等于的时候会求不对，但最后会修正对的，最右的相等元素的右记录一定是对的

答案 §

func largestRectangleArea(heights []int) int {
	ans := 0
	n := len(heights)
	stack := make([]int, 0, n)
	for i, num := range heights {
		for len(stack) > 0 && num <= heights[stack[len(stack)-1]] {
			top := stack[len(stack)-1]
			stack = stack[:len(stack)-1]
			left := -1
			if len(stack) > 0 {
				left = stack[len(stack)-1]
			}
			ans = max(ans, heights[top]*(i-left-1))
		}
		stack = append(stack, i)
	}
	for i := len(stack) - 1; i >= 0; i-- {
		top := stack[i]
		left := -1
		if i-1 >= 0 {
			left = stack[i-1]
		}
		ans = max(ans, heights[top]*(n-left-1))
	}
	return ans
}

题目5.最大矩形 §

题目描述 §

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

测试链接 §

85.最大矩形

思路 §

数组压缩技巧：求以每一行为底的最大矩形，同 题目4

答案 §

func maximalRectangle(matrix [][]byte) int {
	n := len(matrix)
	m := len(matrix[0])
	ans := 0
	for i := 0; i < n; i++ {
		// 来到 i 行，长方形一定要以 i 行做底
	    // 加工高度数组(压缩数组)
		for j := 0; j < m; j++ {
			matrix[i][j] = matrix[i][j] - '0'
			if matrix[i][j] != 0 && i > 0 {
				matrix[i][j] += matrix[i-1][j]
			}
		}
		ans = max(ans, largestRectangleArea(matrix[i], m))
	}
	return ans
}
 
func largestRectangleArea(heights []byte, n int) int {
	ans := 0
	stack := make([]int, 0, n)
	for i, num := range heights {
		for len(stack) > 0 && num <= heights[stack[len(stack)-1]] {
			top := stack[len(stack)-1]
			stack = stack[:len(stack)-1]
			left := -1
			if len(stack) > 0 {
				left = stack[len(stack)-1]
			}
			ans = max(ans, int(heights[top])*(i-left-1))
		}
		stack = append(stack, i)
	}
	for i := len(stack) - 1; i >= 0; i-- {
		top := stack[i]
		left := -1
		if i-1 >= 0 {
			left = stack[i-1]
		}
		ans = max(ans, int(heights[top])*(n-left-1))
	}
	return ans
}