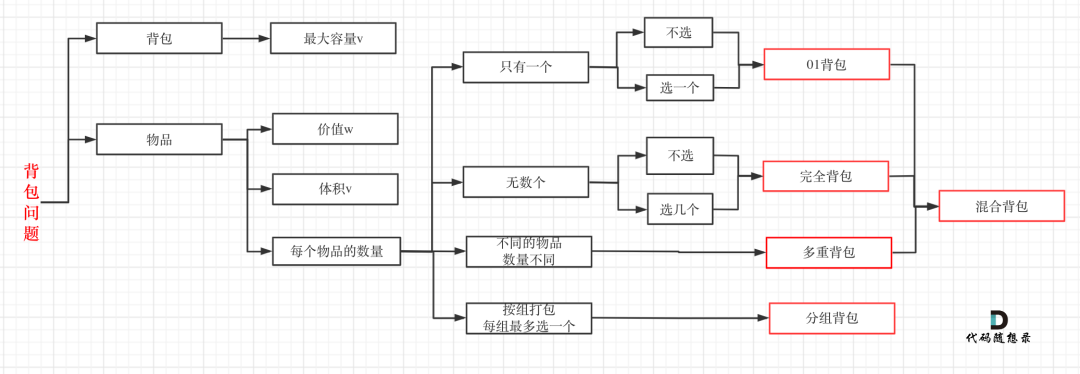
01 背包
- 416.分割等和子集
- 相似题目
- 698.划分为 k 个相等的子集
- 473.火柴拼正方形
- 1723.完成所有工作的最短时间
- 2305.公平分发饼干(同上题)
- 相似题目
- 1049.最后一块石头的重量 II
- 494.目标和
- 474.一和零
完全背包
多重背包
有 N 种物品和一个容量为 V 的背包。第 i 种物品最多有 Mi 件可用,每件耗费的空间是 Ci ,价值是 Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量,且价值总和最大。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有 Mi 件可用,把 Mi 件摊开,其实就是一个01背包问题了。
for i, weight := range weights { // 遍历物品
for j := bagWeight; j >= weight; j-- { // 遍历背包容量
// 以上为01背包,然后加一个遍历个数
for k := 1; k <= nums[i] && (j - k * weight) >= 0; k++ { // 遍历个数
dp[j] = max(dp[j], dp[j - k * weight] + k * value[i]);
}
}
}划分为 k 个相等的子集 - 状态压缩 + 记忆化搜索

var (
theNums []int
theAvg int
theDp []bool
)
func canPartitionKSubsets(nums []int, k int) bool {
sum := 0
for _, num := range nums {
sum += num
}
if sum % k != 0 {
// 不能整除
return false
}
avg := sum / k
sort.Ints(nums)
n := len(nums)
if nums[n - 1] > avg {
// 最大数比平均值大
return false
}
// dp[S]: 数组可用状态为i时,是否可以划分为k个相等的子集
// s: 位图,代表数组每一位的可用状态,1-可用,0-不可用
dp := make([]bool, 1 << n)
for i := range dp {
dp[i] = true
}
theNums = nums
theAvg = avg
theDp = dp
return dfs((1 << n) - 1, 0)
}
/*
s: 位图,代表数组每一位的可用状态,1-可用,0-不可用
pre: 上一步累加的数
*/
func dfs(s, pre int) bool {
if s == 0 {
// 数组每一位都用完
return true
}
if !theDp[s] {
return false
}
theDp[s] = false
for i, num := range theNums {
if pre + num > theAvg {
// 剪枝(数组要升序)
break
}
if (s >> i) & 1 > 0 && dfs(s ^ (1 << i), (pre + num) % theAvg) {
return true
}
}
return false
}划分为 k 个相等的子集 - 状态压缩 + 动态规划

func canPartitionKSubsets(nums []int, k int) bool {
sum := 0
for _, num := range nums {
sum += num
}
if sum % k != 0 {
// 不能整除
return false
}
avg := sum / k
sort.Ints(nums)
n := len(nums)
if nums[n - 1] > avg {
// 最大数比平均值大
return false
}
// dp[S]: 数组可用状态为i时,是否可以划分为k个相等的子集
// s: 位图,代表数组每一位的可用状态,1-可用,0-不可用
dp := make([]bool, 1 << n)
dp[0] = true
curSum := make([]int, 1 << n)
for i, ok := range dp {
if !ok {
continue
}
for j, num := range nums {
if num + curSum[i] > avg {
// 剪枝(数组要升序)
break
}
if (i >> j) & 1 == 0 {
// nums[j] 没用过
next := i | (1 << j)
if !dp[next] {
curSum[next] = (curSum[i] + num) % avg
dp[next] = true
}
}
}
}
return dp[(1 << n) - 1]
}火柴拼正方形
func makesquare(matchsticks []int) bool {
sum := 0
for _, l := range matchsticks {
sum += l
}
// 剪枝:不能被 4 整除
if sum % 4 != 0 {
return false
}
avg := sum / 4
sort.Ints(matchsticks)
n := len(matchsticks)
// 剪枝:不能折断火柴
if matchsticks[n - 1] > avg {
return false
}
dp := make([]bool, 1 << n)
dp[0] = true
curSum := make([]int, 1 << n)
for i, ok := range dp {
if !ok {
continue
}
for j, l := range matchsticks {
if l + curSum[i] > avg {
break
}
if i & (1 << j) == 0 {
next := i | (1 << j)
if !dp[next] {
curSum[next] = (curSum[i] + l) % avg
dp[next] = true
}
}
}
}
return dp[(1 << n) - 1]
}完成所有工作的最短时间

func minimumTimeRequired(jobs []int, k int) int {
n := len(jobs)
m := 1 << n
// sum[j]: j情况下,把工作安排给一个工人,需要的最短时间
// j: 位图,工作安排情况,0-未被分配,1-已被分配
sum := make([]int, m)
for i := 1; i < m; i++ {
// 当前要安排的工作 index
x := bits.TrailingZeros(uint(i))
y := i ^ (1 << x)
sum[i] = sum[y] + jobs[x]
}
// 或
/*
for i, v := range jobs {
for j, bit := 0, 1 << i; j < bit; j++ {
sum[bit | j] = sum[j] + v
}
}
*/
// dp[i][j]: 安排i+1个工人,工作安排为j情况下,需要的最短时间
dp := make([][]int, k)
for i := range dp {
dp[i] = make([]int, m)
}
for i, s := range sum {
dp[0][i] = s
}
for i := 1; i < k; i++ {
for j := 0; j < m; j++ {
minn := math.MaxInt64
for x := j; x > 0; x = (x - 1) & j {
// max(dp[i - 1][j - x] 或 max(dp[i - 1][j ^ x] 都行
minn = min(minn, max(dp[i - 1][j - x], sum[x]))
}
dp[i][j] = minn
}
}
return dp[k - 1][m - 1]
}滚动数组
func minimumTimeRequired(jobs []int, k int) int {
n := len(jobs)
m := 1 << n
sum := make([]int, m)
for i := 1; i < m; i++ {
x := bits.TrailingZeros(uint(i))
y := i ^ (1 << x)
sum[i] = sum[y] + jobs[x]
}
dp := make([]int, m)
copy(dp, sum)
for i := 1; i < k; i++ {
for j := m - 1; j > 0; j-- { // 注意这里的顺序
for x := j; x > 0; x = (x - 1) & j {
dp[j] = min(dp[j], max(dp[j ^ x], sum[x]))
}
}
}
return dp[m - 1]
}爬楼梯
func climbStairs(n int) int {
// 完全背包 - 排列
// 可以解决一次可以爬任意个台阶问题
stairs := [...]int{ 1, 2 }
dp := make([]int, n + 1)
dp[0] = 1
for i := 0; i <= n; i++ { // 背包
for _, stair := range stairs { // 物品
if i - stair >= 0 {
dp[i] += dp[i - stair]
}
}
}
return dp[n]
}零钱兑换
func coinChange(coins []int, amount int) int {
// dp[i]: amount 为 i 时,需要的最少硬币数
dp := make([]int, amount + 1)
dp[0] = 0
for i := 1; i <= amount; i++ {
dp[i] = amount + 1
}
for _, coin := range coins {
for j := coin; j <= amount; j++ {
// +1: 加一个面值为 coin 的硬币
if dp[j - coin] != amount + 1 {
dp[j] = min(dp[j], dp[j - coin] + 1)
}
}
}
if dp[amount] == amount + 1 {
return -1
}
return dp[amount]
}单词拆分 - 回溯 1
var (
theS string
theWordDict []string
n int
)
func wordBreak(s string, wordDict []string) bool {
theS = s
theWordDict = wordDict
n = len(s)
return backtracking(0)
}
func backtracking(start int) bool {
if start == n {
return true
}
for _, word := range theWordDict {
wordLen := len(word)
if start + wordLen > n {
continue
}
if theS[start:start + wordLen] == word {
if backtracking(start + wordLen) {
return true
}
}
}
return false
}单词拆分 - 回溯 2
var (
theS string
n int
wordDictSet map[string]bool
state []int // state[i]: s[i:?] -1-未知,0-不可被拆分,1-可被拆分
)
func wordBreak(s string, wordDict []string) bool {
theS = s
n = len(s)
wordDictSet = make(map[string]bool, len(wordDict))
for _, word := range wordDict {
wordDictSet[word] = true
}
state = make([]int, n)
for i := range state {
state[i] = -1
}
return backtracking(0)
}
func backtracking(start int) bool {
if start >= n {
return true
}
if state[start] == 1 {
return true
}
if state[start] == 0 {
return false
}
for i := start + 1; i <= n; i++ {
curS := theS[start: i]
if wordDictSet[curS] && backtracking(i) {
state[start] = 1
return true
}
}
state[start] = 0
return false
}单词拆分 - 动态规划
func wordBreak(s string, wordDict []string) bool {
n := len(s)
wordDictSet := make(map[string]bool, len(wordDict))
for _, word := range wordDict {
wordDictSet[word] = true
}
dp := make([]bool, n + 1)
dp[0] = true
for i := 1; i <= n; i++ {
for j := 0; j < i; j++ {
if dp[j] && wordDictSet[s[j:i]] {
dp[i] = true
break
}
}
}
return dp[n]
}优化
func wordBreak(s string, wordDict []string) bool {
n := len(s)
dp := make([]bool, n + 1)
dp[0] = true
for i := 1; i <= n; i++ {
for _, word := range wordDict {
wordSize := len(word)
if i >= wordSize && dp[i - wordSize] && s[i - wordSize:i] == word {
dp[i] = true
break
}
}
}
return dp[n]
}